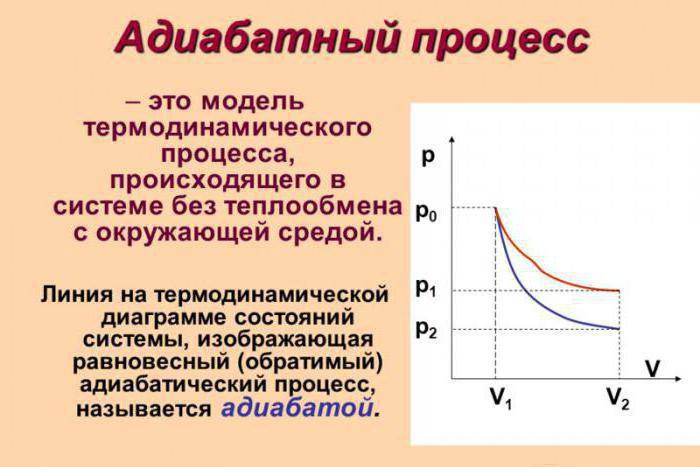
Proces adiabatyczny, jego istota i formuły

Proces adiabatyczny (określany jako adiabatyczny w niektórych źródłach) jest procesem termodynamicznym, który zachodzi przy braku wymiany ciepła z otoczeniem. Jest kilka czynników, które charakteryzują tę klasę. Na przykład proces adiabatyczny zachodzi dynamicznie i jest ustanawiany w krótkim okresie czasu. Z reguły są to procesy tej klasy.

Połączenie z pierwszą zasadą termodynamiki

Proces adiabatyczny (adiabatyczny) może być bezpośrednio związany z pierwsza zasada termodynamiki. Sformułowanie "domyślnie" brzmi następująco: zmiana ilości ciepła w układzie podczas procesu termodynamicznego w nim będzie liczbowo równa sumie energii wewnętrznej gazu doskonałego i pracy wykonanej przez ten gaz.

Jeśli próbujemy pisać pierwsze uruchomienie termodynamiki w swojej standardowej postaci otrzymujemy następujące wyrażenie: dQ = dU + dA. A teraz spróbujemy zmodyfikować tę formułę w odniesieniu do procesu adiabatycznego. Jak wspomniano wcześniej, takie procesy zachodzą pod warunkiem braku wymiany ciepła z otoczeniem (zewnętrznym, jak nazywają to niektóre źródła literackie) medium.

W takim przypadku wzór opisujący pierwszą zasadę termodynamiki przyjmie następującą postać: dA = -dU. Teraz trochę więcej o modyfikacji. Jeśli powiemy, że nie ma wymiany ciepła w układzie, zmiana ilości ciepła (wskazana we wzorze pierwszej zasady termodynamiki przez dQ) będzie zerowa. W związku z tym możemy przenieść jeden z dodatków z prawej na lewą, po czym uzyskamy formułę zredukowaną do formy opisanej wcześniej.

Następstwo pierwszego prawa termodynamiki dla procesu adiabatycznego

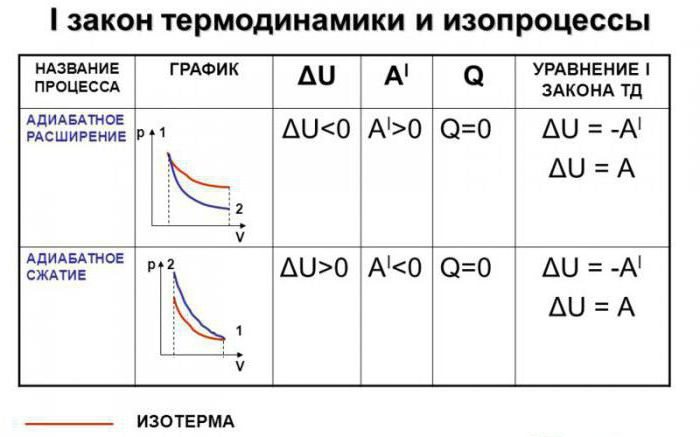
Załóżmy, że w systemie wystąpił proces adiabatyczny. W tym przypadku możliwe jest, bez wchodzenia w najdrobniejsze szczegóły, stwierdzenie, że gaz wykonuje pracę podczas rozszerzania, ale jednocześnie traci wewnętrzną energię. Innymi słowy, praca wykonywana podczas adiabatycznego rozprężania gazu będzie prowadzona z powodu utraty energii wewnętrznej. W konsekwencji, w wyniku tego procesu, rozważymy spadek temperatury samej substancji.

Absolutnie logiczne jest założenie, że jeśli gaz zostanie skompresowany adiabatycznie, jego temperatura wzrośnie. Łatwo zauważyć, że w trakcie procesu wszystkie główne cechy gazu doskonałego ulegną zmianie. Chodzi o jego ciśnienie, objętość i temperaturę. Dlatego nazwa procesu adiabatycznego przez proces izoprocesowy stała się poważnym błędem.

Proces adiabatyczny. Formuły

Formuła wywodząca się z pierwszej zasady termodynamiki została spisana wcześniej. Za jego pomocą możemy łatwo obliczyć pracę, którą gaz będzie wykonywał podczas procesu adiabatycznego. Jak mogliście się domyślić, zrobimy to za pomocą integracji.

Aby więc uzyskać ogólną formułę pracy dla x moli gazu, integrujemy ekspresję pierwszej zasady termodynamiki dla procesu adiabatycznego. Wszystko to będzie wyglądać następująco: A = - (całka) z dU. Otwieramy to wyrażenie, otrzymujemy: A = - xCv (całka od T1 do T2) dT.

Teraz, gdy wprowadziliśmy całkę do skończonej formy, możemy ją uprościć. Na wyjściu otrzymujemy następującą formułę: A = - xCv (T2 - T1). Cóż, ostatnim krokiem będzie niewielkie uproszczenie. Pozbywamy się minus przed formułą. Aby to zrobić, wykonujemy małą permutację w nawiasach, zmieniając końcową temperaturę z początkowymi miejscami. W rezultacie otrzymujemy: A = xCv (T1 - T2).

Równanie adiabatyczne

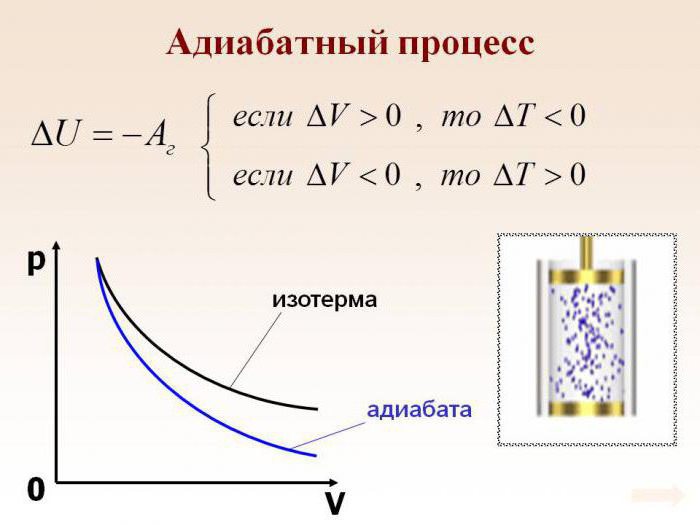
Używając pierwszej zasady termodynamiki dla procesu adiabatycznego, możemy znaleźć równanie adiabatyczne. Jednocześnie zostanie on zarejestrowany dla dowolnej liczby moli gazu doskonałego. Tak więc zapisujemy oryginalną formułę. Wygląda to tak: dA + dU = 0. Ale doskonale wiemy, że praca z idealnym gazem nie jest niczym więcej jak produktem zmiany ciśnienia i objętości.

W tym samym czasie zmienić energia wewnętrzna będzie równa pracy wykonanej z przeciwnym znakiem. I już to znaleźliśmy dzięki integracji. Stąd pierwsza zasada termodynamiki dla procesu adiabatycznego może przyjąć następującą postać: pdV + xCvdT = 0. Musimy wykluczyć jeden wskaźnik z tego równania, a mianowicie temperaturę. Przeciwnie, jego zmiany. Aby to zrobić, zwracamy się do równania, które jest często używane w fizyce molekularnej. Mianowicie, równanie Mendelejewa-Clapeyrona.

Pierwotne wyrażenie

Musimy to rozróżnić, co zrobimy. Ogólnie mówiąc, równanie jest następujące: PV = XRT. Ze względu na różnicowanie zostanie ono zredukowane do następującej postaci: pdV + Vdp = xRdT. Stąd możemy wyrazić zmianę energii. Będzie równy lewej części podzielonej przez iloczyn ilości substancji i uniwersalnej stałej gazowej. Innymi słowy, formuła byłaby następująca: (pdV + Vdp) / xR. Pozostaje tylko go uprościć. W rezultacie otrzymujemy następujące wyrażenie: dT = (pdV + Vdp) / x (Cp - Cv)

W rzeczywistości pierwsza część zadania została zakończona. Pozostaje tylko pamiętać wszystko.

Wyrażenie wtórne Podstawianie wartości

Weźmy formułę Mendeleeva-Clapeyrona otrzymaną w wyniku różnicowania i zastąpmy ją wyrażeniem, które wyprowadziliśmy wcześniej dla pierwszej zasady termodynamiki w odniesieniu do procesu adiabatycznego. Więc co otrzymujemy? Cała ta uciążliwa ekspresja przyjmuje następującą postać: pdV + xCv ((pdV + Vdp) / x (Cp-Cv)) = 0.

Aby uprościć to wszystko, musimy wziąć pod uwagę kilka faktów. Po pierwsze, wyrażenie można uprościć, redukując je do wspólnego mianownika. Kiedy dostaniemy jedną frakcję, możemy użyć starej dobrej reguły, która mówi, że ułamek wynosi zero, gdy jego licznik wynosi zero, a mianownik jest niezerowy. W wyniku kombinacji wszystkich tych działań otrzymujemy następujące wyrażenie: pCpdV - pCvdV + pCvdV + VCvdp = 0.

Teraz kolejnym krokiem jest podzielenie tego wyrażenia na pVCv. Otrzymujemy sumę dwóch części, co daje zero. Będzie to Cp / Cv * dV / V + dp / p = 0. Ta formuła musi być zintegrowana. Otrzymujemy następujące wyrażenie: y (całka) dV / V + (całka) dp / p = (całka) 0.

Cóż, wszystko jest proste. Używając formuł integracyjnych (można użyć całek tabelarycznych, aby wszystko było prostsze), otrzymujemy następujący wpis: y ln V + ln p = ln (const). Okazuje się, że p (V) y = const. W fizyce molekularnej to wyrażenie nazywa się równaniem Poissona. Wiele źródeł naukowych nazywa tę formułę równaniem adiabatycznym. W tym samym czasie wartość y, która występuje w tym rekordzie, nazywana jest indeksem adiabatycznym. Jest równa (i + 2) / i. Należy zauważyć, że indeks adiabatyczny jest zawsze większy niż jeden, co z zasady jest logiczne.

Przykłady procesów adiabatycznych

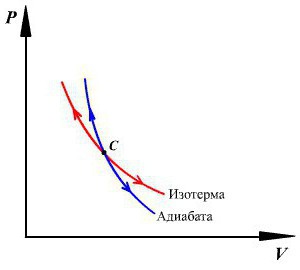
Wkrótce po odkryciu procesu adiabatycznego rozpoczęto ogromną liczbę różnych badań. W ten sposób powstał pierwszy teoretyczny model związany z cyklem Carnota. To ona pozwoliła na ustanowienie warunkowych ograniczeń ograniczających rozwój silników cieplnych. Ale w przypadku niektórych rzeczywistych procesów do przeprowadzenia Cykl Carnota wystarczająco mocno. Chodzi o to, że składa się z izoterm. A one z kolei wymagają ustawienia pewnego tempa procesów termodynamicznych.

Wniosek

Aby ominąć takie problemy, wynaleziono cykl Otto, a także cykl skraplanie gazu. Stały się one szeroko stosowane w rozwiązywaniu konkretnych problemów w praktyce. Rozpoczęte badania pokazały możliwość opisania pewnych naturalnych procesów w płaszczyźnie adiabatycznej, co umożliwiło identyfikację ogólnych wzorców odpowiednich procesów. Przykład procesu adiabatycznego można nazwać reakcją chemiczną, która zachodzi wewnątrz pewnej objętości gazu, jeśli układ jest zamknięty i nie ma wymiany ciepła ze środowiskiem zewnętrznym.