Kombinatoryka - co to jest? Elementy kombinatoryki
Specjaliści w różnych dziedzinach muszą rozwiązywać problemy kombinacyjne: przegrupowanie liczb, znaków i innych obiektów. Na przykład kierownik sklepu musi dystrybuować różne rodzaje pracy między działającymi maszynami. Kombinatoryka jest znaczącą gałęzią matematyki, która, jak nietrudno zgadnąć, znajduje swoją niszę w różnych dziedzinach i specjalnościach: fizyka, biologia, lingwistyka, chemia, inżynieria, teoria kodowania i wiele innych. Zasady kombinatoryki leżą u podstaw rozwiązania zestawu probabilistycznych problemów.
Historia
Pierwsze warunki wstępne kombinatoryki jako nauki pojawiły się w XVI wieku. Przyczynił się do rozwoju tego obszaru wiedzy w dużym stopniu, fascynacji ludzi hazardem: kartami, kostkami, loterią straconą nie tylko złotem i klejnotami, ale także pałacami i majątkami. Dlatego zastanawiając się, na przykład, jak często można rzucić dobry zestaw punktów na kości lub uzyskać dwa asy, ludzie stopniowo doszli do podstaw kombinatoryki i prawdopodobieństwa. Czy kombinatoryka pomogła komuś wygrać więcej lub stracić mniej? Pytanie jest interesujące, ale jego rozważania wykraczają poza zakres tego artykułu.
Ad

Pierwszym matematykiem, który był aktywnie zainteresowany kombinatoryką, był włoska Włoszka Tartaglia (1499-1557), a po nim tak wybitni uczeni jak Pascal, Fermat, Bernoulli, Leibnitz, Euler i inni aktywnie zanurzali się w badaniu tych zagadnień, jednak warto zauważyć, że nadal pozostało, jeśli nie jest zabawną grą z liczbami, to teoria, która jest używana wyłącznie w grach hazardowych i nie ma prawa być używana gdzie indziej.
Rozwój kombinatoryki
Znaczące postępy w kombinatorykach miały miejsce wraz z nadejściem XX wieku. komputery, programowanie i co najważniejsze - dyskretna matematyka. W tym czasie kombinatoryka osiąga szczyt swojego szybkiego rozwoju i staje się pełnoprawną nauką. Metody kombinatoryczne zaczynają być używane wszędzie:
Ad
- rozwiązanie problemów transportowych;
- planowanie;
- przygotowywanie planów produkcji i sprzedaży towarów;
- w teorii procesów losowych;
- w statystykach matematycznych i teorii prawdopodobieństwa;
- w przygotowaniu i przeprowadzeniu eksperymentów;
- w szachach;
- w termodynamice;
- w geometrii;
- oraz w wielu innych obszarach.
Superstitious Leader Challenge
Na świecie był przywódca, który uważał, że liczba 8 przynosi mu całkowite porażki. Dlatego postanowił pozbyć się wszystkich liczb, które zawierałyby cyfrę ósemkową. Pod jego opieką pracowało 600 osób. Wszyscy mieli numer identyfikacyjny przejść do pracy, składający się z trzech liczb. Nie zastanawiając się dwa razy, menedżer zdecydował się wykluczyć liczbę 8 z liczby karnetów, a następnie zastanawiał się, czy jest wystarczająco dużo różnych liczb dla 600 osób z przedziału od 000 do 999, które nie obejmowałyby 8?
Oczywistym rozwiązaniem tego problemu jest ręczne zapisanie wszystkich liczb od 000 do 999 i wykreślenie tych, w których jest ich osiem. Czy możliwe jest rozwiązanie problemu w prostszy sposób? Jeśli dla 999 liczb, zadanie z wyliczeniem wszystkich wariantów wygląda na wykonalne, wówczas zakres od 000000 do 999999 będzie wymagał znacznie większego wysiłku. Ma to na celu oszczędność czasu i wysiłku zaprojektowanych formuł kombinatoryki.
Ad
Rozwiązanie problemu zabobonnego przywódcy
Inne rozwiązanie jest następujące. Eliminując 8 z serii, otrzymujemy 0, 1, 2, 3, 4, 5, 6, 7, 9 - te dziewięć liczb jest poprawnych. Po tym, powinieneś znaleźć wszystkie dwucyfrowe liczby, które nie zawierają 8. To jest po prostu: musisz wziąć dowolny numer z ważnego i dodać do niego również dowolny numer z ważnego. W ten sposób z łatwością otrzymamy wszystkie dwucyfrowe liczby, które pasują do warunku. W rezultacie uzyskujemy, że każda pojedyncza cyfra da 9 różnych liczb dwucyfrowych. Całkowita liczba takich cyfr będzie 9 * 9 = 9 2 = 81.
Kontynuując analogię, możemy wywnioskować, że aby uzyskać wszystkie liczby trzycyfrowe bez ósemek, konieczne jest przypisanie trzeciej cyfry do istniejących dwucyfrowych liczb, także z dozwolonych wartości. Wtedy otrzymamy informację, że liczba takich liczb będzie wynosić 9 2 * 9 = 9 * 9 * 9 = 729. W ten sposób dowiedzieliśmy się, że szef naszego szefa łatwo będzie w stanie zapewnić 600 pracownikom luki, których liczby nie będą zawierać. 8. Spróbuj rozwiązać problem dla siebie z pięciocyfrowymi numerami.
A co się stanie, jeśli menedżer nie polubi numeru 2? Okazuje się, że liczba dopuszczalnych liczb będzie wynosiła 8, a mianowicie: 0, 1, 3, 4, 5, 6, 7, 9. Następnie, po oszacowaniu liczby kombinacji liczb bez 2 i 8, możemy wywnioskować, że ich liczba to 8 * 8 * 8 = 512, a to zdecydowanie nie wystarcza, aby zapewnić 600 osobom przepustki. Kombinatoryka jest nauką, która pomaga odpowiedzieć na takie pytania skuteczniej niż można to zrobić za pomocą brutalnej siły.
Ad
Problem z lotto
Wszyscy znają tę grę. Jest torba, w której znajdują się beczki o numerach od 1 do 90. Bilety są rozdawane wszystkim uczestnikom, w których konieczne jest namalowanie pewnej liczby komórek za pomocą liczb. Po tym, wiodący loteryjka wyjdzie z torby jedną z ponumerowanych beczek. Zwycięzcą zostanie ten, kto przekroczył większość numerów w bilecie, co pokrywa się z tymi, które gospodarz gry wyciągnął.

Raz Nina, grając w lotto, pomyślała. Często obserwowała, jak prezenter pobiera ten sam numer z torby. Ale w tym samym czasie pierwsze dwie beczki okazały się tym samym znacznie rzadziej. Potem zastanawiała się, na ile sposobów można konsekwentnie wyjąć dwie beczki z torby? Elementy kombinatoryki pomagają odpowiedzieć na jej pytanie.
Rozwiązanie Lotto
Oczywiście, pierwsza beczka może mieć numery od 1 do 90. Innymi słowy, istnieje 90 sposobów na wyodrębnienie pierwszej beczki. Ale co dalej? Jeśli na przykład beczka nr 63 została wyjęta z torby, to w bieżącej grze już się to nie powtórzy.
Metoda tabeli pomoże nam rozwiązać problem. Gdzie w nagłówku i nagłówku kolumny zostaną zapisane liczby od 1 do 90. Tak więc na przecięciu dowolnej linii i dowolnej kolumny będzie para cyfr lub para beczek usuniętych z torby. W tym samym czasie na przekątnej stołu będą znajdować się te same pary liczb. Co jest niemożliwe w zależności od warunku, ponieważ po usunięciu z torby jednej cyfry niemożliwe jest jego powtórzenie. Uzyskaj tabelę w następującym formularzu:
Ad
| 1 | 2 | ... | 90 | |
| 1 | x | 1, 2 | ... | 1, 90 |
| 2 | 2, 1 | x | ... | 2, 90 |
| ... | ... | ... | x | ... |
| 90 | 90, 1 | 90, 2 | ... | x |
Łącznie otrzymujemy tabelę, w której liczba komórek wynosi 90 * 90 = 8100. Należy pamiętać, że na przekątnej znajduje się 90 par cyfr, co jest niemożliwe w zależności od warunków. Następnie odpowiedź na pytanie, na ile sposobów można uzyskać 2 beczki z worka będzie 8100 - 90 = 8010 opcji.
Rozumowanie w nieco inny sposób można dojść do tej samej odpowiedzi. W przypadku pierwszej beczki dostępnych jest 90 opcji. Po wyodrębnieniu pierwszej opcji pozostanie 89 opcji dla drugiej beczki. Tak więc łączna liczba opcji będzie wynosić 90 * 89 = 8010. Elementy kombinatoryki mogą być używane na różne sposoby. Jedynym pytaniem jest prostota i uniwersalność metody. Na przykład, metoda ta może być użyta do wydobycia trzech beczek z rzędu i oczywiście będzie to limit. A co dla czterech lub więcej?
Problem z załogą
Jeśli wybory zależą od tego, które obiekty zostały wybrane wcześniej, wygodnie jest wyświetlić taki proces jako "drzewo". W pierwszym kroku wiele linii jest ułożonych z jednego punktu, ponieważ w pierwszym kroku możliwe są wybory. Na końcach każdej linii znajduje się również tyle dodatkowych linii, ile można zrobić w drugim kroku, itp. W rezultacie zostanie narysowany rodzaj drzewa lub wykresu. Kombinatoryka i teoria mogą wydawać się dość mylące i niezrozumiałe, więc spójrzmy na przykład.
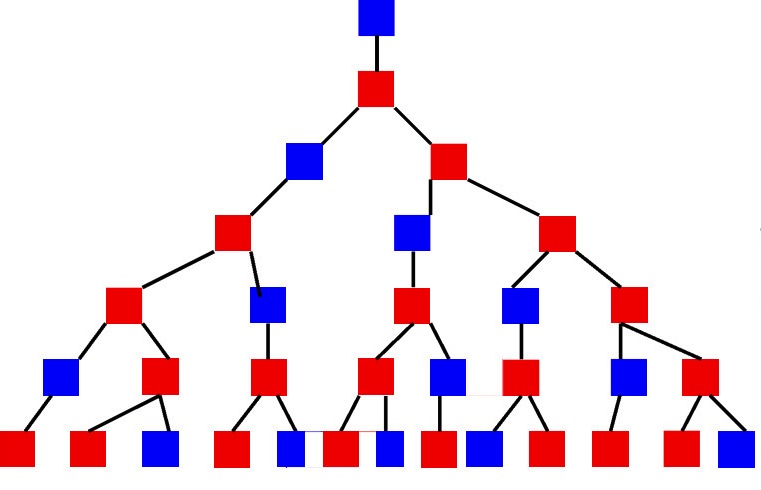
Przed rozpoczęciem roku ekspedycyjnego kierownictwo ma zadanie - zebrać załogi na wycieczki. Każda drużyna musi składać się z trzech osób: dowódcy, inżyniera i lekarza. W tym samym czasie liczba specjalistów w danym obszarze może być różna. Dopuszcza się na przykład, że jednego lekarza wysyła się na dwie różne wyprawy, ponieważ jest tylko dwóch lekarzy, aw każdym dowódcy i inżynierze może być trzech. W tym przypadku kompilator planu ekspedycyjnego musi wziąć pod uwagę psychologiczną kompatybilność członków zespołu. Ta cecha jest jedną z najważniejszych w długich i odległych wyprawach dla ich udanego zachowania. Na podstawie wszystkich opisanych warunków pojawia się następujący obraz:
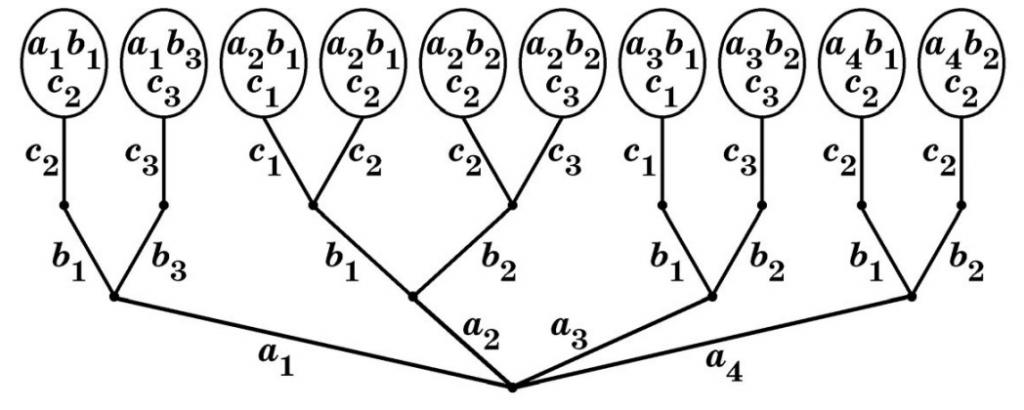
Gdzie ja jestem dowódcą, b ja jestem inżynierem, a ja jestem lekarzem. W tym samym czasie, podczas testowania każdej osoby, okazało się, że dowódca 1 psychicznie dobrze dogaduje się z inżynierami b 1 i b 3 , a 2 - z b 1 i b 2 , ale lekarz c 3 jest niezgodny z inżynierem b 1 , itp. Pytanie, które zostało pierwotnie postawione kierownikowi projektu, to ile zespołów może być skomponowanych w takich warunkach. Z wykresu widać, że w sumie może być 10 takich załóg, ale co by się stało, gdyby kwestia zgodności psychologicznej nie miała znaczenia? Następnie okazuje się, że po wyborze dowódców a, dla każdego z nich przy wyborze inżyniera byłyby 3 alternatywy. W związku z tym, dla pary dowódców i inżynierów, byłyby również 3 opcje dla lekarzy. Wtedy liczba kombinacji osiągnie 4 * 3 * 3 = 36 załóg.
Miejsca docelowe, permutacje i kombinacje
W powyższych przykładach rozwiązanie problemów nastąpiło dzięki tak zwanej metodzie aksjomatycznej. Oznacza to, że można powiedzieć, że istnieje szereg podstawowych zadań, których rozwiązanie można zredukować do wielu problemów. Jednakże, podobnie jak w stereometrii, niewygodne jest rozwiązywanie problemów opartych wyłącznie na aksjomatach, a do tego celu służy wygodniejsze narzędzie zwane "twierdzeniami", więc w kombinatoryce wygodniej jest stosować bardziej uogólnione i sprawdzone metody. W trakcie wielowiekowego badania kombinatoryki stało się oczywiste, że wiele zadań napotyka się częściej niż inne i zostały one podzielone na osobne klasy i otrzymały ich nazwy, stając się główną kombinatoryczną - mianowicie stacjami, permutacjami i kombinacjami.

Problemy kombinatoryczne
Jednym z kluczowych problemów metod kombinatorycznych jest ustalenie, który zestaw zadań należy uznać za kombinatoryczny. Nie można tego ściśle zdefiniować ze względu na ogromną różnorodność problemów, które należą do kategorii kombinatorycznej. A wiele zadań może dotyczyć kombinatoryki, a także innej dziedziny, sąsiadującej lub granicznej.

W uproszczonym przypadku można zauważyć, że matematyka kombinatoryczna obejmuje problemy dotyczące próbek i lokalizacji obiektów. Jednocześnie kombinatoryka charakteryzuje się pracą wyłącznie z skończonym zestawem obiektów. Na podstawie tych przepisów możemy wyróżnić następujące zadania charakterystyczne dla kombinatoryki:
- Dokonaj wyboru obiektów, biorąc pod uwagę wszelkie właściwości.
- Udowodnić lub obalić istnienie próbki pod pewnymi warunkami.
- Znajdź liczbę możliwych kombinacji.
- Znajdź wszystkie kombinacje i określ algorytm ich wyliczenia.
- Znajdź optymalne rozwiązanie problemu w danych warunkach.
Jeśli dany problem można przypisać do jednego z tych typów, to jest kombinatoryczny, a formuły kombinatoryczne pomogą go rozwiązać.