Aktualna moc w obwodach elektrycznych
Jednym z parametrów charakteryzujących zachowanie elektronów w obwodzie elektrycznym, oprócz napięcia i prądu, jest moc. Jest to miara ilości pracy, jaką można wykonać w jednostce czasu. Praca jest zwykle porównywana do podnoszenia ciężaru. Im większy ciężar i wysokość jego wzrostu, tym więcej pracy jest wykonywanych. Moc określa prędkość jednostki pracy.
Jednostki miary
Moc samochodu obliczana jest w postaci mocy - jednostki miary wymyślonej przez producentów silniki parowe w celu zmierzenia wydajności ich jednostek w zwykłym źródle energii czasu. Moc samochodu nie mówi, jak wysoko może dotrzeć do wzniesienia ani ile waga może unieść, ale pokazuje tylko, jak szybko to zrobi.
Ad
Moc silnika zależy od prędkości i momentu obrotowego wału wyjściowego. Prędkość jest mierzona w obrotach na minutę. Moment obrotowy jest momentem mocy silnika, który początkowo był mierzony początkowo w funtach i teraz w metrach lub dżinach.
100 litrowy silnik ciągnika c. obraca się powoli, ale z dużym momentem obrotowym. Silnik motocykla o równej mocy wiruje szybko, ale z niewielkim momentem obrotowym. Równanie obliczania mocy ma postać:
P = 2π ST / 33000, gdzie S oznacza prędkość obrotową, obr / min, a T oznacza moment obrotowy.
Zmienne to tu moment i prędkość. Innymi słowy, moc jest wprost proporcjonalna do ST: P ~ ST.
Moc prądu stałego
W obwodach elektrycznych moc jest zależna funkcjonalnie od napięcia i prądu. Nic dziwnego, że jest podobny do powyższego równania P = IU.
Ale tutaj P nie jest proporcjonalne do prądu pomnożonego przez napięcie, ale jest równe temu. Oblicza się ją w watach, w skrócie W.
Ważne jest, aby wiedzieć, że prąd i napięcie osobno nie określają mocy, a jedynie ich połączenie. Napięcie to praca na jednostkę ładunek elektryczny a prąd jest prędkością opłat. Napięcie (odpowiednik roboczy) jest podobne do pracy przy podnoszeniu ciężaru w opozycji do siły grawitacji. Prąd (równoważny prędkości) jest podobny do prędkości podnoszenia ciężaru. Ich praca to moc.
Ad
Podobnie jak w silnikach traktorów i motocykli, obwód wysokiego napięcia z małym prądem może mieć taką samą moc jak obwód niskiego napięcia i duży prąd. Napięcie i prąd poza układem nie mogą charakteryzować mocy obwodu.
Otwarty obwód z napięciem i zerowym natężeniem nie działa, niezależnie od wysokości napięcia. Wszakże zgodnie ze wzorem, wszystko pomnożone przez 0 daje 0: P = 0 U = 0. W obwodzie zamkniętym drutu nadprzewodzącego o zerowej rezystancji, prąd można uzyskać przy napięciu równym zeru, co również nie prowadzi do rozpraszania energii: P = I 0 = 0.
Moc i waty oznaczają jedno i to samo: ilość pracy jaką można wykonać w jednostce czasu. Jednostki te są powiązane przez stosunek
1 l. c. = 745,7 W
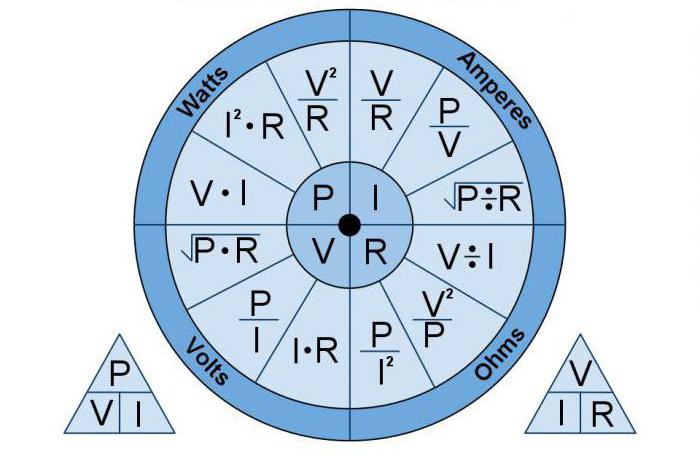
Przykład kalkulacji
Tak więc moc prądu obwodu elektrycznego w watach jest równa iloczynowi napięcia i prądu.
Aby określić, na przykład, moc obciążenia o rezystancji 3 omy, w obwodzie z akumulatorem 12 V, konieczne jest, stosując prawo Ohma, znalezienie aktualnego prądu
I = U / R = 12/3 = 4 A
Mnożenie prądu za pomocą napięcia i uzyskanie pożądanego rezultatu:
P = IU = 4 A 12 V = 48 W
Tak więc lampa zużywa 48 watów.
Co dzieje się, gdy napięcie wzrasta?
Przy napięciu 24 V i rezystancji 3 Ω prądu
I = U / R = 24/3 = 8 A
Po podwojeniu napięcia natężenie prądu podwoiło się.
P = IU = 8 A 24 V = 192 W
Moc również wzrosła, ale więcej. Dlaczego? Ponieważ jest to funkcja iloczynu napięcia na prąd, napięcie i natężenie wzrosły 2 razy, dlatego moc wzrosła 4 razy. Można to zweryfikować, dzieląc 192 watów na 48, których iloraz wynosi 4.
Ad
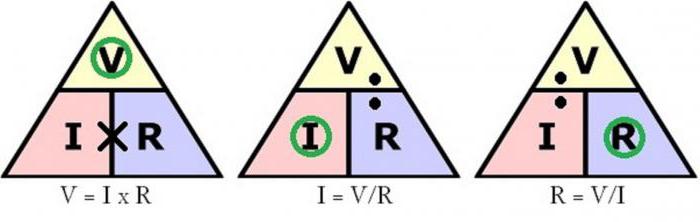
Warianty formuły
Używając algebry do przekształcenia formuły, możesz pobrać oryginalne równanie i przekształcić je w przypadkach, w których jeden z parametrów jest nieznany.
Jeżeli podano napięcie i rezystancję:
P = (U / R) U lub P = U 2 / R
Ze znaną siłą i oporem prądu:
P = I (IR) lub P = I 2 R
Fakt historyczny: związek pomiędzy rozproszoną mocą i prądem przez opór odkrył James Prescott Joule, a nie Georg Simon Om. Zostało wydane w 1841 roku jako równanie P = I 2 R i nazywane jest prawem Joule - Lenz.
Równania mocy:
- P = UI
- P = I 2 R
- P = U 2 / R
Prąd przemienny
Ustawa o Ohmie i Dżulu - Lenz została ustanowiona dla prąd stały ale są one również ważne dla chwilowych wartości zmiennego prądu i napięcia.
Wartość chwilowa P jest równa iloczynowi chwilowych wartości prądu i napięcia, biorąc pod uwagę ich przesunięcie fazowe o kąt φ:
P (t) = U (t) I (t) = U m cos ω I m cos (ωt-φ) = (1/2) U m I m φ φ + (1/2) U m I m cos (2ω- φ).
Z równania wynika, że chwilowa moc ma stały składnik i powoduje ruchy oscylacyjne wokół średniej wartości z częstotliwością dwukrotnie większą od częstotliwości prądu.

Średnia wartość P (t), która ma znaczenie praktyczne, wynosi:
P = (U m Jestem m / 2) cosφ
Biorąc pod uwagę, że cos φ = R / Z, gdzie Z = (R 2 + (ω L - 1 / ω C) 2 ) 1/2 i U m / Z = I m ,
P = (RI m 2 ) / 2
Tutaj I = I m 2 -1/2 = 0,707 I m - efektywna wartość prądu natężenia, A.
Podobnie U = U m 2 -1/2 = 0,707 U m - efektywne napięcie, V.
Średnia moc na efektywnym napięciu i natężeniu jest określona przez
P = UI cos φ, gdzie cos φ jest współczynnikiem mocy.
P w obwodzie elektrycznym przechodzi w ciepło lub inną formę energii. Najwyższą moc czynną można uzyskać za pomocą cosφ = 1, czyli bez przesunięcia fazowego. Nazywa się to pełną mocą.
S = UI = ZI2 = U2 / Z
Jego wymiar pokrywa się z wymiarem P, ale dla celu różnicy S jest mierzony woltamperami, VA.
Stopień wymiany energii w obwodzie elektrycznym charakteryzuje moc bierna.
Q = UI sinφ = UI p = U p I = XI 2 = U 2 / X
Ma wymiar aktywny i kompletny, ale w celu jego rozróżnienia wyrażany jest za pomocą reaktywnych woltamperów, VAR.
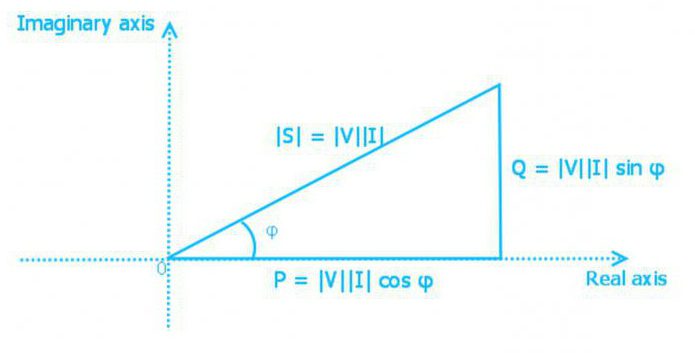
Trójkąt mocy
Moc jest aktywna, reaktywna i pełna połączona przez
S = (P 2 + Q 2 ) 1/2
Moc reprezentuje jako stronę trójkąt prostokątny. Używając praw trygonometrii, można znaleźć długość jednej strony (ilość mocy dowolnego typu) wzdłuż dwóch znanych boków lub wzdłuż długości jednego i kąta. W takim trójkącie moc czynna to sąsiednia noga, moc bierna jest przeciwna, a całkowita moc jest przeciwprostokątna. Kąt między aktywnym odgałęzieniem mocy a przeciwprostokątną jest równy kątowi fazowemu impedancji Z obwodu elektrycznego.
Ad
Złożona forma tej zależności wygląda następująco:
S = P + jQ = UI cosφ + j UI sinφ = UI e jφ = UI *, gdzie
S to złożona moc;
I * to złożona wartość prądu sprzężonego.
Prawdziwym składnikiem kompleksu jest aktywny, a wyobrażony jest reaktywny.
Natychmiastowa całkowita moc zawsze pozostaje stała.
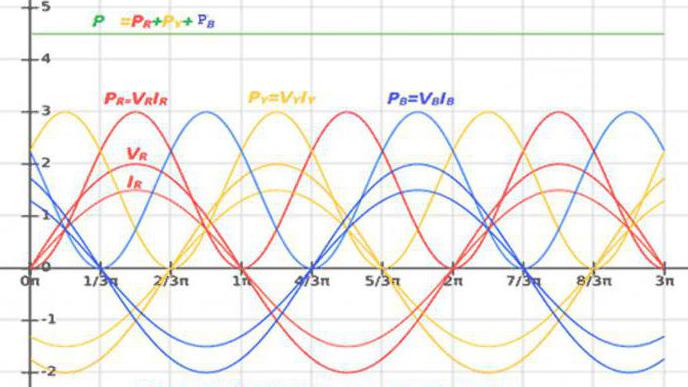
Moc trójfazowa
Obciążenie każdej fazy trójfazowego obwodu przetwarza energię lub wymienia ją na źródło prądu. W rezultacie obwody P i Q są równe całkowitej mocy wszystkich faz:
P = P r + P y + P b ; Q = Q r + Q y + Q b - połączenie w gwiazdę;
P = P ry + P yb + P br ; Q = Q ry + Q yb + Q br - połączenie "trójkąt".
Aktywne i bierne moce każdej fazy są zdefiniowane jako w obwodzie jednofazowym.
Pełna moc obwodu trójfazowego:
S = (P 2 + Q 2 ) 1/2 ,
jak wygląda złożona forma
S = P + jQ = (P r + P y + P b ) + j (Q r + Q y + Q b ) = S r + S y + S b = U r I r + U y I y + U b I b
Symetryczne ładowanie faz skutkuje równością ich mocy. Właśnie dlatego moc prądu jest trzy razy większa niż moc czynna i bierna fazy:
P = 3P f = 3 I f U f cosφ f = 3 R f I f 2
Q = 3 Q f = 3 I f U f sinφ f = 3 X f I f 2
S = 3 S f = 3 I f U f
I f i U f tutaj można zastąpić ich wartościami liniowymi, biorąc pod uwagę, że dla gwiazdy U f = U l ; I f = I l , a dla trójkąta U f = U l ; I f = I l 3 -1/2 :
P = 3 1/2 I l U l cosφ f ;
Q = 3 1/2 I l U l sinφ f ;
S = 3 1/2 I l U l .
Prąd niesinusoidalny
Definicja P w niesinusoidalnym obwodzie prądowym jest podobna do jego definicji w sinusoidalnym obwodzie prądowym, ponieważ przez okres T średnia chwilowa moc
P = 1 / T∫ui dt
Aktywna moc prądu jest określona przez sumę składowych harmonicznych P, w tym stałą, która jest harmoniczną częstotliwości zerowej.
Moc bierna prądu w ten sposób jest wynikiem dodania Q każdej harmonicznej.
Q = ΣU k I k sinφ k = Q k
Całkowita moc jest określana przez iloczyn skutecznego prądu i napięcia:
S = I U.