Zasada Dirichleta: problemy z rozwiązaniami
W matematyce istnieje wiele zasad. Niektóre z nich są dość proste i zrozumiałe nawet dla początkujących, a niektóre wymagają pewnych wyjaśnień i dowodów. Wszystkie są jednak bardzo skuteczne i można je łatwo zastosować w praktyce. Jedną z nich jest zasada Dirichleta (znana również jako zasada gołąb / królik). Jest to dość proste stwierdzenie, które może pomóc w rozwiązaniu wielu problemów matematycznych.

Historia
Zasada ta została sformułowana przez honorowego niemieckiego matematyka Johanna Dirichleta w 1834 roku. Dziś jest używany w kombinatoryce, a także w fizyce matematycznej. Przetłumaczone z oryginalnego niemieckiego, brzmi jak "zasada pudełek". Naukowiec przeprowadził swoje badania z królikami i pojemnikami. Wykazał, że jeśli umieścimy, powiedzmy, 5 królików w 7 pojemnikach, to przynajmniej w jednym pojemniku będzie 5/7 od jednego zwierzęcia. Królika nie można jednak podzielić na części, dlatego przynajmniej jedna komórka będzie pusta (5/7 to 0 liczb całkowitych). W ten sam sposób, w przeciwnym kierunku, jeśli jest 7 królików i 5 pudełek, to przynajmniej jeden z nich ma 2 króliki (7/5 jest 2 nienaruszone). Poczynając od tego stwierdzenia, matematyka zdołała sformułować zasadę, która od wielu lat zapewnia skuteczne rozwiązywanie problemów w matematyce.
Ad
Nowoczesne sformułowania i dowód
Obecnie istnieje kilka różnych sformułowań tej zasady. Najbardziej zrozumiały i prosty sposób oznacza, że nie można zasadzić 8 królików w 3 klatkach tak, aby każda z nich miała nie więcej niż 2. Bardziej naukowe i złożone sformułowanie wyjaśniające zasadę Dirichleta mówi: jeśli w komórkach k znajduje się k + 1 królików, to przynajmniej Co najmniej 1 komórka będzie zawierać więcej niż jednego zająca. A jeśli w komórkach k występują k-1 zające, to przynajmniej 1 komórka zawiera mniej niż jeden zając. Dowód tego stwierdzenia jest dość prosty, że tak powiem, przez sprzeczność. Jeśli przyjmiemy, że w każdej komórce jest mniej zajęcy niż k-1 / k, wówczas k komórek zajęczych jest mniejsza niż k * k-1 / k = k-1, co jest sprzeczne z warunkami początkowymi.
Ad
W rzeczywistości taka prosta i zrozumiała zasada znacznie ułatwia rozwiązanie problemów w matematyce i dowód wielu żmudnych twierdzeń. Trzeba tylko wziąć pod uwagę, że zające i komórki można łatwo zastąpić matematycznymi obiektami i obiektami (liczby, punkty, segmenty, liczby itp.).
Inne sformułowanie
Czasami zadania na zasadzie Dirichleta nie są tak proste i oczywiste, jak w przypadku zwierząt w pudełkach. Konieczne jest przeniesienie tej zasady do zbiorów matematycznych w celu znalezienia jakichkolwiek rozwiązań. W takim przypadku możesz polegać na innym, bardziej złożonym sformułowaniu. 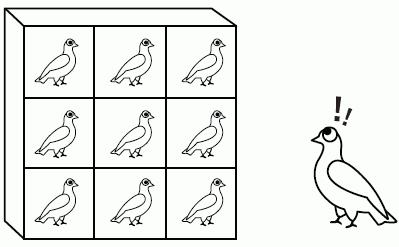
Jeśli zmapujemy zbiór S zawierający elementy d + 1 do zbioru R z zestawem elementów d, to dwa elementy z zestawu S będą miały ten sam obraz.
Chociaż współczesna GEF w matematyce narzuca twórcze wymagania uczniom i oferuje niestandardowe opcje, rozwiązanie dzięki twierdzeniu Dirichleta nie zawsze jest takie proste i proste. Czasami bardzo trudno jest określić, jaką wartość uznać za zwierzę, a która jako klatka, i jak fakt posiadania dwóch zwierząt w jednej klatce pomaga rozwiązać problem. A jeśli uda nam się to rozgryźć, nadal niemożliwe jest ustalenie, w której konkretnej komórce będzie ten obiekt. Oznacza to, że możesz po prostu udowodnić istnienie takiej komórki, ale nie możesz jej skonkretyzować.
Ad
Numer przykładu 1. Geometria
Współczesne przykłady rozwiązywania problemów pokazują, że doskonałe różne obiekty matematyczne mogą działać jak zwierzęta i komórki.
Zadanie
Linia k przechodzi przez płaszczyznę trójkąta ABC, ale nie przecina żadnego z jej wierzchołków. Konieczne jest udowodnienie, że nie może przekroczyć trzech stron.
Rozwiązanie
Wyobraź sobie, jak linia k dzieli trójkąt na dwie płaszczyzny, nazwijmy je s1 i s2. Zakładamy, że s1 i s2 są otwarte, to znaczy nie zawierają linii k. Teraz nadszedł czas na zastosowanie zasady Dirichleta. Zadania z rozwiązaniami mogą pokazać, że w nowoczesnych warunkach króliki i komórki oznaczają różne obiekty. Zamiast zajęć zastępujemy wierzchołki trójkąta, a zamiast komórek - pół-płaszczyzny. Ponieważ narysowana linia k nie przecina żadnego z wierzchołków, każdy z nich jest w jednej lub drugiej płaszczyźnie. Ale ponieważ w trójkącie są trzy wierzchołki, a mamy tylko dwie płaszczyzny (s1 i s2), jedna z nich będzie zawierać dwa wierzchołki. Załóżmy, że są to wierzchołki A i B, i są one w połowie płaszczyzny s2 (to znaczy leżą po tej samej stronie k). W tym przypadku odcinek AB nie przecina prostej K. Oznacza to, że w trójkącie jest bok, którego k nie przecina się.
Ad
Alternatywne rozwiązanie
W tym problemie przyjęliśmy, że punkty A i B znajdują się w tej samej płaszczyźnie, ale zasada Dirichleta nie wskazuje konkretnej komórki, więc możemy również wskazać, że wierzchołki C i B lub A i C znajdowały się w tej samej płaszczyźnie. nie ma znaczenia, która strona trójkąta przecina się z linią prostą k. Dlatego ta zasada jest idealna dla swojego rozwiązania.
Przykład nr 2. Geometria
Zadanie
W środku trójkąta równobocznego ABC (w którym AB = BC = AC = 1) zlokalizowano 5 punktów. Konieczne jest udowodnienie, że dwa z nich znajdują się w odległości mniejszej niż 0,5.
Rozwiązanie
Jeśli narysujesz środkowe linie w prawym trójkącie ABC, podzielą go na 4 małe trójkąty prostokątne o bokach ½ = 0,5. Załóżmy, że te trójkąty są komórkami, a punkty wewnątrz nich to króliki. Okazuje się, że mamy 5 królików i 4 komórki, dlatego w jednym z nich będą co najmniej dwa króliki. Biorąc pod uwagę, że punkty nie są wierzchołkami (ponieważ znajdują się wewnątrz trójkąta ABC, a nie po jednej ze stron), zostaną umieszczone wewnątrz małych figur. W konsekwencji odległość między nimi będzie mniejsza niż 0,5 (ponieważ rozmiar segmentu wewnątrz trójkąta nigdy nie przekracza rozmiaru jego największego boku).
Numer przykładu 3. Kombinatoryki
W innych dziedzinach zasada Dirichleta może być z powodzeniem stosowana: kombinatoryka i fizyka matematyczna od dawna opierają się na rozwiązywaniu problemów.
Zadanie
Na przykład wokół okrągłego stołu flagi różnych krajów znajdują się w równej odległości od siebie, a m reprezentanci każdego kraju siedzą przy stole, każdy z nich znajduje się obok flagi innej osoby. Konieczne jest udowodnienie, że przy pewnym obrocie stołu co najmniej dwóch przedstawicieli będzie blisko swoich flag.
Ad
Rozwiązanie
Okazuje się, że istnieje m-1 sposobów na poszerzenie tabeli, tak aby wzajemne ustawienie reprezentantów i flag zmieniło się (jeśli wykluczymy początkowe umieszczenie stołu), ale zostało m przedstawicieli.
Zastosujemy asercję Dirichleta do rozwiązania i oznaczamy, że przedstawiciele są królikami, a niektóre pozycje tabel podczas obrotu są komórkami. W tym przypadku konieczne jest narysowanie analogii między położeniem przedstawiciela obok odpowiedniej flagi i wypełnionych komórek. Oznacza to, że wynik pozytywny (1 przedstawiciel znajduje się w pobliżu jego flagi) jest równoważny wynikowi "królik jest w klatce". Rozumiemy, że mamy jedną komórkę mniej niż to, co jest potrzebne (m-1), co oznacza, że jeden z nich będzie miał co najmniej 2 króliki. Jednocześnie nie wyklucza się sytuacji, w których część klatki będzie pusta (nie jeden przedstawiciel pasuje do flagi), ale w pewnej klatce będą dwa, trzy lub nawet więcej króliki (dwóch, trzech lub więcej przedstawicieli zbiegnie się z flagami). Tak więc, przy jednym pewnym obrocie, co najmniej dwóch przedstawicieli znajdzie się w pobliżu swoich flag (co najmniej dwa króliki wpadną do jednej komórki).
Rozpoczynając rozwiązanie takiego problemu, ważne jest, aby zrozumieć, że pozycja początkowa jest również komórką, ale w zależności od stanu problemu jest ona oczywiście pusta, więc zmniejszamy sumę o 1 (m-1).
Numer przykładu 4. Teoria liczb
Zasada Dirichleta w teorii liczb ma również ogromne znaczenie.
Zadanie
Załóżmy, że na kawałku notesu w klatce student losowo w węzłach komórek odłożył 5 punktów. Konieczne jest udowodnienie, że co najmniej jeden segment z wierzchołkami w tych punktach przechodzi przez węzeł komórki.
Rozwiązanie
Najpierw musisz zobrazować na arkuszu notebooka układ współrzędnych, którego podstawę znajduje się w jednym z węzłów. Osie układu współrzędnych pokrywają się z liniami siatki, a strona komórki jest traktowana jako pojedynczy segment. Okazuje się, że wszystkie 5 zaznaczonych punktów będzie w systemie, a ich współrzędne będą tylko liczbą całkowitą (parzystą lub nieparzystą). Otrzymujemy 4 opcje współrzędnych: (parzyste, parzyste), parzyste, parzyste, parzyste, nieparzyste i nieparzyste. Tak więc 2 na 5 punktów będzie odpowiadać jednemu wariantowi. Jeśli spojrzysz na sytuację z pozycji Dirichleta, musisz wyznaczyć punkty jako zające, a opcje współrzędnych - jako komórki. Dostajemy 5 ptaków z jednym kamieniem i 4 klatkami odpowiednio, w jednym z nich będą co najmniej 2 zwierzęta. Załóżmy, że są to punkty P i A o współrzędnych (x 4 , y 3 ) i (x 5 , y 6 ). Środek segmentu łączącego te dwa wierzchołki będzie miał współrzędne ((x 4 + x 5 ) / 2), ((y 3 + y 6 ) / 2)), które będą liczbami całkowitymi w warunkach odpowiadającej parzystości x 4 i x 5, y 3 i y 6 . Okazuje się, że środek segmentu znajduje się w węźle komórki.
Numer przykładu 5
Sporo zadań o różnej złożoności można rozwiązać za pomocą zasady Dirichleta. Problemy z rozwiązaniami różnych pytań matematycznych i logicznych często opierają się na tej zasadzie.
Zadanie
Na prostej drodze wykopali małe poprzeczne rowki. Odległość między wszystkimi rowkami jest taka sama i równa Ö2 m. Konieczne jest udowodnienie, że niezależnie od szerokości rowków, osoba przechodząca wzdłuż drogi w odstępach 1 m wpadnie raz na jeden z nich.
Rozwiązanie
Aby ułatwić rozwiązanie, należy sobie wyobrazić, że droga może być "nawinięta" na okrąg o długości Ö 2 metrów. Okazuje się, że wszystkie rowki scalą się w 2 przeciwległe, a kroki osoby będą wyświetlane w postaci łuku równego 1 m. Musimy kolejno zaznaczać wszystkie stopnie, aż jeden z nich znajdzie się w łuku oznaczającym rowek, bez względu na długość k łuk (szerokość rowka). Oczywiście oczywiste jest, że jeśli mężczyzna przeszedłby dystans równy mniej niż k, to wcześniej czy później znalazłby się w rowie. W końcu osoba nie może przekroczyć dystansu k, jeśli jego długość kroku jest mniejsza niż k. Musimy więc znaleźć dwie ścieżki, których odległość nie przekroczy wartości k. Aby to zrobić, należałoby zastosować zasadę Dirichleta. W myślach dzielimy całe koło na łuki o wielkości mniejszej niż k, a my uznamy je za komórki. Załóżmy, że jest ich n. Załóżmy, że liczba kroków jest większa niż liczba łuków (n + m), chociaż żadne dwa kroki nie będą się pokrywać z powodu irracjonalności liczby Ö2, a następnie zgodnie z zasadą Dirichleta, przynajmniej jedna z komórek będzie zawierała więcej niż jeden krok. A ponieważ długość łuku jest mniejsza niż k, odległość pomiędzy krokami będzie mniejsza. W związku z tym znaleźliśmy kroki niezbędne do przeprowadzenia dowodu. 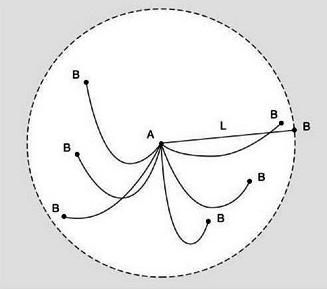
Uogólnienie zasady
Materiały matematyczne, oprócz standardowych (prostych i niezbyt wysokich) formuł, zawierają także jeden uogólniony, który służy do identyfikacji więcej niż dwóch obiektów podobnych do siebie. Twierdzi, że jeśli dm + 1 królików zostanie umieszczonych w komórkach d, to przynajmniej m + 1 królików będzie w tej samej komórce.
Przykład nr 6. Uogólnienie
Zadanie
Prostokąt o powierzchni 5 x 6 komórek (30 komórek), tylko cieniowany 19. Czy można znaleźć kwadrat o powierzchni 2 x 2 komórki, w którym co najmniej trzy zostaną zamalowane?
Rozwiązanie
Nasza liczba musi być podzielona na 6 bloków po 5 komórek. Na podstawie stwierdzenia Dirichleta w jednym z nich zostanie namalowane co najmniej 4 komórki (19/6 = 4). Następnie na jednym z kwadratów o powierzchni 4 komórek, znajdujących się w jednym z bloków, zostaną zamalowane co najmniej 3 komórki.
Numer przykładu 7
Klasa, w której 25 osób. Z dowolnych 3 losowo wybranych uczniów, dwoje będzie przyjaciółmi. Konieczne jest udowodnienie, że w klasie jest uczeń, który ma więcej niż 11 przyjaciół.
Dwa rozwiązania

Na początek zabieramy dwoje dzieci w wieku szkolnym, które nie są ze sobą przyjaźnie nastawione (ponieważ gdyby wszystkie były ze sobą przyjaźnie, w każdej trojce byłoby trzech przyjaciół, a każdy uczeń byłby zaprzyjaźniony z 24 innymi). Pozostali 23 koledzy z klasy będą zaprzyjaźnić się z jednym z naszych dwóch, ponieważ w przeciwnym razie pojawi się trojka bez przyjaciół (a to przeczy oryginalnemu stanowi problemu). Okazuje się, że jeden z dwóch studentów zaprzyjaźni się z co najmniej 12 studentami. W tym przypadku uczniowie są królikami, a terminy "przyjaciele lub nie" to komórki. Mamy 23 zwierzęta i tylko 2 klatki. Odpowiednio, w jednym z nich co najmniej 23/2 = 11,5, to znaczy 12 królików. Oznacza to, że jeden z dwóch wybranych przez nas studentów będzie przyjaźnie z co najmniej 12 kolegami z klasy (lub nawet więcej). Oczywiście istnieją inne metody rozwiązania problemu, ale jest to jedna z najbardziej zrozumiałych i wygodnych.