Dynamika i kinematyka ruchu kołowego: formuły i rozwiązanie typowego problemu

Umiejętność opisania ruchu w kole jest ważna dla obliczenia parametrów technicznych obracających się wałów i kół zębatych. Ten rodzaj ruchu występuje również w życiu codziennym i przyrodzie, np. Obracanie się planet wokół słońca i łyżwiarzy podczas występów na zawodach sportowych. W tym artykule rozważymy, jak z punktu widzenia fizyki można opisać ten rodzaj ruchu.

Dynamika rotacji

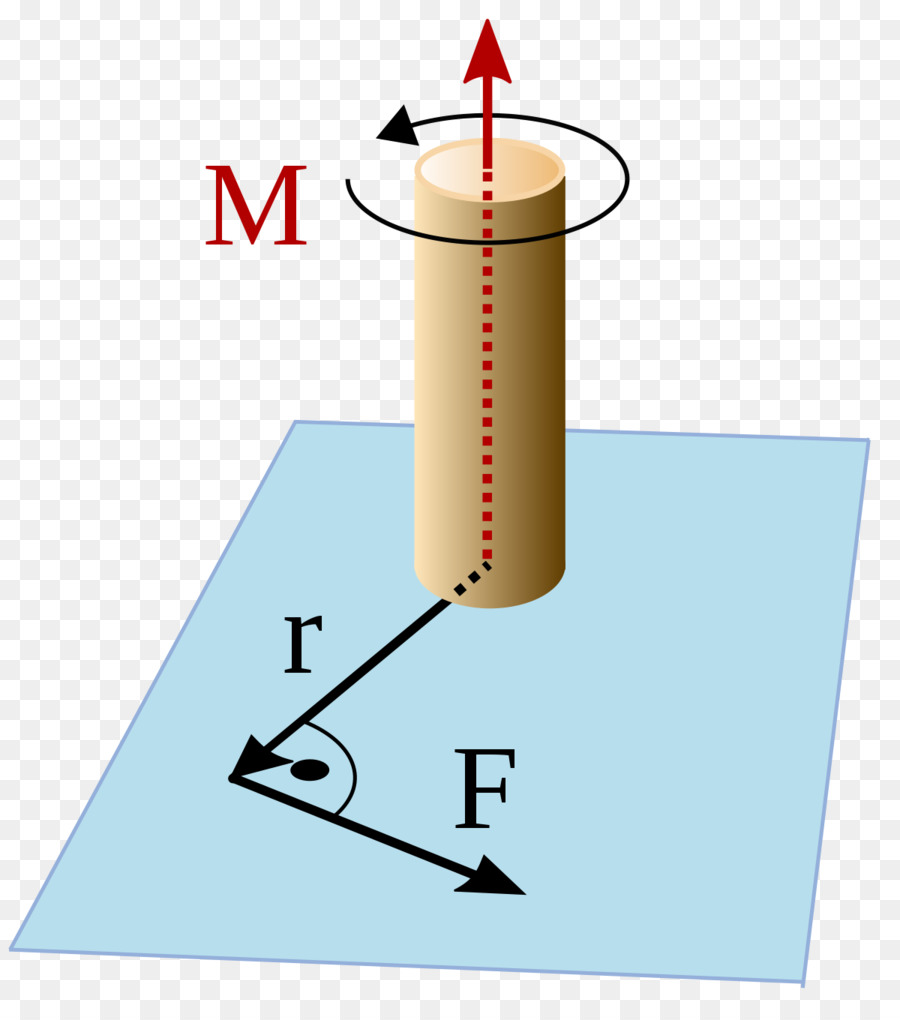
Ruch w okręgu to obrót określonego ciała lub punktu materialnego wokół osi. Aby ciało zaczęło się obracać, konieczny jest zewnętrzny moment obrotowy działający na dany układ. Moment ten jest określony przez formułę:

M = F * d

Tutaj F jest siłą, d jest długością dźwigni (odległość między osią a punktem przyłożenia siły). Moment siły jest wartością wektorową. Formuła służy do obliczenia modułu M.

Wpływ momentu M odbija się na układzie w postaci pojawienia się przyspieszenia kątowego. Oznacza to, że system zaczyna się obracać. Główna formuła ruchu kołowego jest zapisana jako:

M = I * α

Tutaj jestem momentem bezwładności, α jest akceleracją kątową. Obie wielkości mają swoje analogi dla przypadku liniowego. Jeśli wszystko jest jasne z analogiem wartości α, to dla momentu bezwładności konieczne jest wyjaśnienie. Wartość I odzwierciedla właściwości bezwładnościowego układu wirującego. Oznacza to, że podczas obrotu odgrywa taką samą rolę jak zwykła masa ciała.

Zauważ, że powyższe wyrażenie jest analogiem drugiego prawa Newtona do rotacji.

Siły dośrodkowe i odśrodkowe, przyspieszenie

Proces rotacji zakłada obecność pewnej siły wewnętrznej, która zapewniłaby ruch krzywoliniowy ciała. Ta siła nazywa się dośrodkowa. Zgodnie z nazwą, zawsze jest kierowana z ciała do osi obrotu. Ponieważ długość dźwigni d dla niej wynosi zero, nie prowadzi to do wystąpienia przyspieszenia kątowego α. Niemniej jednak zmienia on wektor prędkości liniowej, czyli tworzy przyspieszenie.

Przyspieszenie w ruchu w okręgu bez zmiany modułu prędkości liniowej nazywa się dośrodkowo. Jest obliczany według wzoru:

a _c = v ² / r

Gdzie v jest prędkością liniową punktu materialnego obracającego się w odległości r od osi.

Oprócz dośrodkowego, często można usłyszeć o sile odśrodkowej. Ten ostatni dąży do sprowadzenia ciała z kolistej ścieżki do linii prostej. Powodem jego występowania są bezwładności systemu wirującego.

Podczas poruszania się w okręgu siły dośrodkowe i siły odśrodkowe są równe sobie wzajemnie w kierunku przeciwnym do siebie.

Kinematyczne równania rotacji

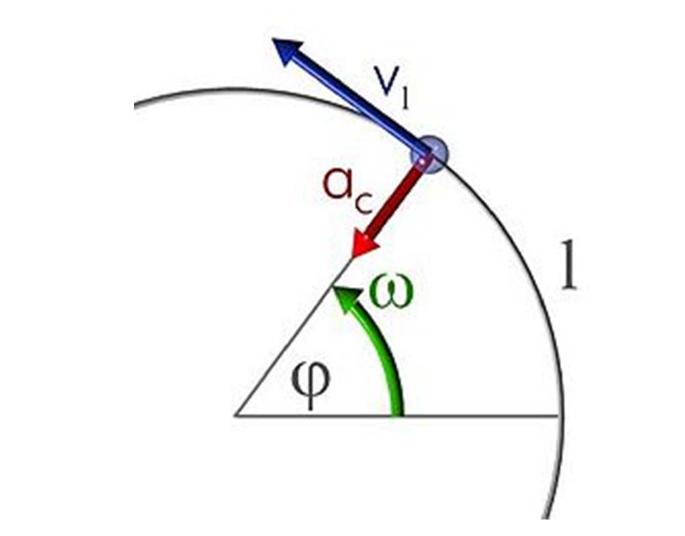
Ruch w okręgu, jak w linii prostej, może być jednorodny lub występować z przyspieszeniem. W pierwszym przypadku formuła to:

θ = ω * t

Oznacza to, że kąt środkowy θ, na którym ciało obraca się w czasie t, jest wprost proporcjonalny do prędkości kątowej ω. Kąt θ wyraża się w radianach, a prędkość ω wyraża się w radianach na sekundę.

Jeśli w systemie działa stały zewnętrzny moment sił, wówczas ruch w okręgu następuje z pewnym stałym przyspieszeniem α. W takim przypadku prawdziwe wyrażenie kinematyczne będzie prawdziwe:

θ = α * t 2/2

Jeśli system najpierw obrócił się z pewną prędkością ω _0, a następnie zaczął zwiększać swoją częstotliwość obrotu z przyspieszeniem α, to począwszy od momentu t, kiedy pojawiło się przyspieszenie, wzór będzie ważny:

θ = ω ₀ * t + α * t 2/2

Zwróć uwagę, że to wyrażenie jest kombinacją liniową dwóch poprzednich.

Związek liniowej i kątowej charakterystyki kinematycznej

Powyżej podano formułę przyspieszenia dośrodkowego, zapisaną liniową prędkością v. Jednak wzór ten można również zapisać w odniesieniu do odpowiedniej charakterystyki kątowej ω.

Załóżmy, że obracające się ciało wykonało jeden obrót wokół koła w czasie t. Następnie dla prędkości liniowych i kątowych możemy napisać:

v = 2 * pi * r / t;

ω = 2 * pi / t

Stąd widać, że moduł prędkości liniowej v jest r razy wielkości magonu ω, czyli:

v = ω * r

Ta równość łączy prędkości kątowe i liniowe. Używając go, możesz napisać formułę dla _c przez ω:

a _c = ω ² * r

Teraz obliczamy w formule z prędkościami pochodną czasu dla lewej i prawej strony równości, otrzymujemy:

dv / dt = dω / dt * r =>

a = α * r

Równość ta łączy przyspieszenie liniowe a skierowane stycznie z okręgiem i jego kątowym analogiem α.

Łatwo jest udowodnić, że centralny kąt obrotu θ podczas poruszania się po okręgu jest związany z długością jego łuku L, z następującym wyrażeniem:

L = θ * r

Tutaj, jeśli θ jest równe 2 * pi radianów (pełny obrót), otrzymujemy długość okręgu L.

Rozwiązanie problemu określania siły dośrodkowej

Wiadomo, że kamień o wadze 0,5 kg został przywiązany do 1-metrowej liny i zaczęli obracać ją z częstotliwością 3 obrotów na sekundę. Konieczne jest znalezienie siły naprężającej liny Fc.

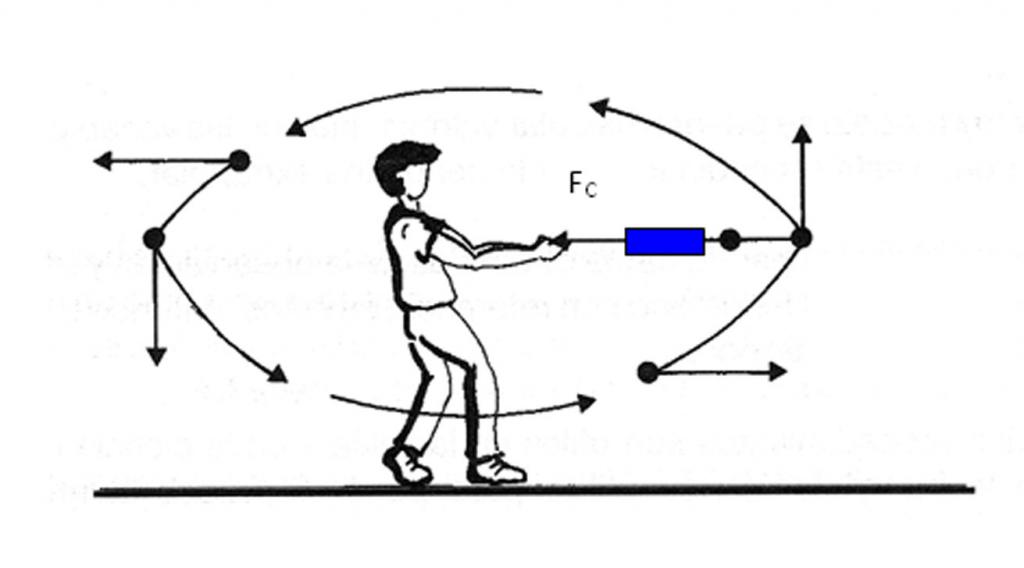
Siła naprężająca Fc jest dośrodkowa. Można go obliczyć według wzoru:

F _c = m * a. _C

Znana jest masa kamienia m. Przyspieszenie dośrodkowe a _c można obliczyć na podstawie znajomości prędkości kątowej ω. Gdy częstotliwość f ustawiona w zadaniu, ilość ω jest powiązana z wyrażeniem:

ω = 2 * pi * f

Następnie przyspieszenie dośrodkowe zostanie obliczone jako:

a _c = 4 * pi ² * f ² * r

Żądana siła F _c będzie równa:

F _c = 4 * pi ² * f ² * r * m

Jeśli warunkiem problemu jest zastąpienie danych w tym wzorze, otrzymamy wartość siły Fc, w przybliżeniu równą 177,5 N.