Stan równowagi dźwigni. Zasada chwil. Proste mechanizmy. Zadania i rozwiązania
Od niepamiętnych czasów ludzkość używa różnych mechanizmów, które mają ułatwiać pracę fizyczną. Jednym z nich jest dźwignia. Co to jest, jaka jest idea jego użycia i jaki jest stan równowagi dźwigni, ten artykuł poświęcony jest rozważaniu wszystkich tych kwestii.
Kiedy ludzkość zaczęła stosować zasadę dźwigni?

Trudno precyzyjnie odpowiedzieć na to pytanie, ponieważ proste mechanizmy znane były już starożytnym Egipcjanom i mieszkańcom Mezopotamii już trzy tysiące lat przed naszą erą.
Jednym z tych mechanizmów jest tak zwany dźwig dźwigowy. Reprezentował długi słup, który znajdował się na podporze. Ten ostatni był zainstalowany bliżej jednego końca słupa. Pod koniec, który znajdował się dalej od punktu odniesienia, przywiązali naczynie, z drugiej postawili przeciwwagę, na przykład kamień. System został dostosowany w taki sposób, że naczynie wypełnione na pół doprowadziło do pozycji poziomej słupa.
Ad
Dźwig dźwigowy służył do podnoszenia wody ze studni, rzeki lub innej depresji do poziomu, na którym znajdowała się osoba. Przez przyłożenie małej siły do naczynia, osoba opuściła ją do źródła wody, naczynie napełniono cieczą, a następnie, stosując niewielką siłę na drugim końcu słupa z przeciwwagą, możliwe było podniesienie wskazanego naczynia.
Legenda o Archimedesie i statku
Każdy zna starożytnego greckiego filozofa z miasta Syracuse, Archimedesa, który w swoich pismach nie tylko opisał zasadę działania prostych mechanizmów (dźwignia, nachylona tablica), ale także zaowocował odpowiednimi formułami matematycznymi. Do dziś jego zdanie pozostaje sławne:
Dajcie mi przyczółek, a ja przeniosę ten świat!

Jak wiecie, nikt nie dał mu takiego wsparcia, a Ziemia pozostała na swoim miejscu. Jednak tym, co Archimedes naprawdę mógł poruszyć, był statek. Jedna z legend Plutarcha (praca "Równoległe życie") mówi: Archimedes w liście do swojego przyjaciela, króla Hierona z Syracuse, powiedział, że pod pewnymi warunkami może poruszać się samodzielnie o arbitralnie dużej wadze. Hieron był zaskoczony takim stwierdzeniem filozofa i poprosił go, aby zademonstrował, o czym mówi. Archimedes zgodził się. W jednym z dni statek Hierona w doku był załadowany ludźmi i beczkami wypełnionymi wodą. Filozof siedzący w pewnej odległości od statku był w stanie unieść go ponad wodę, ciągnąc za liny, przy niewielkim wysiłku.
Składniki dźwigni
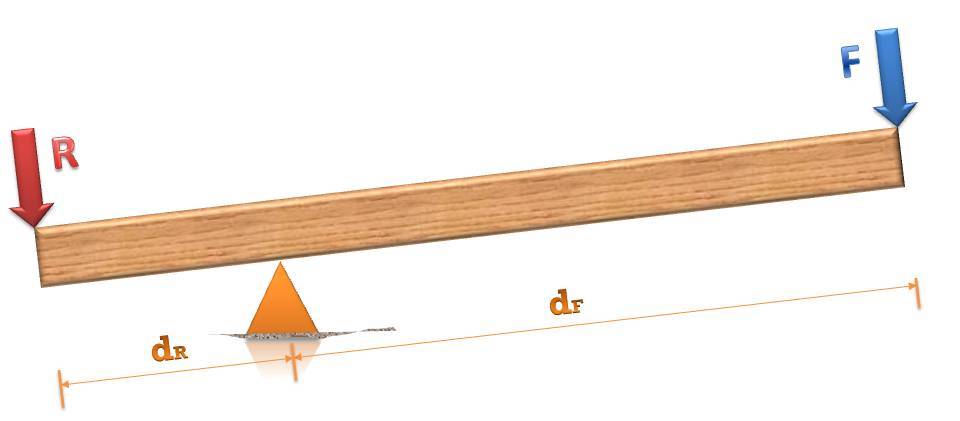
Pomimo tego, że mówimy o dość prostym mechanizmie, wciąż ma pewne urządzenie. Fizycznie składa się z dwóch głównych części: słupa lub belki i podpory. Rozważając te same zadania, biegun jest traktowany jako obiekt składający się z dwóch (lub jednego) ramion. Ramię jest częścią słupa, która jest względem podpory z jednej strony. Dużą rolą w zasadzie działania rozpatrywanego mechanizmu jest dokładnie długość barku.
Rozważając dźwignię w pracy, pojawiają się dwa dodatkowe elementy: zastosowana siła i moc, aby temu przeciwdziałać. Pierwsza dąży do uruchomienia obiektu, który tworzy siłę sprzeciwu.
Ad
Stan równowagi dźwigni w fizyce
Zapoznawszy się z urządzeniem tego mechanizmu, przedstawiamy wzór matematyczny, za pomocą którego możemy powiedzieć, które ramię dźwigni przesunie się w którym kierunku, lub odwrotnie, całe urządzenie będzie w spoczynku. Formuła ma postać:
F 1 * l 1 = F 2 * l 2 ,
gdzie F 1 i F 2 to siły działania i reakcji, l 1 i l 2 to długości ramion, do których te siły są przyłożone.
Wyrażenie to pozwala badać warunki równowagi dźwigni o osi obrotu. Jeśli więc ramię l 1 jest większe niż l 2 , to aby zrównoważyć siłę F 2, potrzebujesz mniejszej wartości F 1 . Wręcz przeciwnie, jeśli l 2 > l 1 , to aby zneutralizować siłę F 2, będziesz musiał dołączyć duży F 1 . Te wnioski można uzyskać, przepisując powyższe wyrażenie w następującej formie:
Ad
F 1 / F 2 = l 2 / l 1 .
Jak widać, siły zaangażowane w proces tworzenia równowagi są odwrotnie proporcjonalne do długości ramion dźwigni.
Jaki jest zysk i strata podczas używania dźwigni?
Z powyższych formuł wynika ważny wniosek: za pomocą długiego ramienia i małego wysiłku można przenosić przedmioty o ogromnej masie. Jest to prawdą i wielu może pomyśleć, że użycie dźwigni prowadzi do zwiększenia pracy. Ale tak nie jest. Praca to ilość energii, której nie można stworzyć z niczego.
Przeanalizujmy pracę prostej dźwigni z dwoma utwardzeniami l 1 i l 2 . Załóżmy, że na końcu ramienia l 2 znajduje się masa ciężaru P (F 2 = P). Na końcu drugiego ramienia osoba przykłada siłę F 1 i podnosi ten ładunek na wysokość h. Teraz obliczyć pracę każdej siły i zrównać uzyskane wyniki. Otrzymujemy:
Ad
F 1 * x = F 2 * godz.
Siła F 2 działała wzdłuż pionowej trajektorii długości h, z kolei F1 działała również wzdłuż pionu, ale była już przymocowana do drugiego ramienia, którego koniec poruszał się o nieznaną wielkość x. Aby go znaleźć, konieczne jest zastąpienie w ostatnim wyrażeniu wzoru połączenia sił i ramion dźwigni. Wyrażając x, mamy:
x = F 2 * h / F 1 = l 1 * h / l 2 .
Ta równość pokazuje, że l 1 > l 2 , a następnie F 2 > F 1 i x> h, to jest przy zastosowaniu małej siły, można podnieść ładunek o dużej wadze, ale trzeba przesunąć odpowiednie ramię dźwigni (l 1 ) do większego. odległość. Wręcz przeciwnie, jeśli l 1 <l 2 , wtedy F 2 <F 1 i x <h, to znaczy, waga określonej wagi może zostać podniesiona do większej wysokości h przez przesunięcie ramienia l 1 do mniejszej amplitudy, ale trzeba zastosować wystarczająco dużą siłę F 1 . W pierwszym przypadku uzyskuje się wzmocnienie, w drugim w drodze lub prędkości.
W związku z tym dźwignia nie przynosi korzyści w pracy, pozwala jedynie na redystrybucję jej albo na korzyść mniejszej siły przykładanej, albo na korzyść większej amplitudy ruchu przedmiotu. Ogólna filozoficzna zasada działa w temacie omawianej fizyki: każdy zysk jest kompensowany pewną stratą.
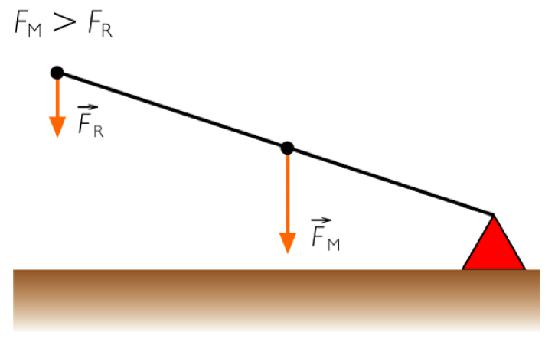
Rodzaje dźwigni
W zależności od punktów przyłożenia siły i położenia podpory wyróżniono następujące typy tego mechanizmu:
- Pierwszy rodzaj: punkt podparcia znajduje się pomiędzy dwiema siłami F 1 i F 2 , a zatem długość ramion określa, co daje taką przewagę. Przykładem są zwykłe nożyczki.
- Drugi rodzaj. W tym przypadku siła, z jaką wykonuje się pracę, znajduje się pomiędzy podporą a zastosowaną siłą. Ten rodzaj konstrukcji oznacza, że zawsze da to przyrost siły i utratę podróży i prędkości. Jego przykładem jest samochód ogrodowy.
- Trzeci rodzaj. Ostatnią opcją, która pozostaje do zrealizowania w tym prostym projekcie, jest położenie przyłożonej siły między podporą a siłą oporową. W tym przypadku zysk na drodze, ale utrata jest w mocy. Przykładem może być pinceta.

Pojęcie momentu siły
Uwzględnianie wszelkich problemów w mechanice, które obejmują pojęcia osi lub punktu obrotu, odbywa się za pomocą reguły siły siły. Ponieważ podparcie dźwigni jest także osią (punktem), wokół której obraca się układ, moment siły służy również do oszacowania równowagi tego mechanizmu. Rozumie się przez to ilość w fizyce, równą iloczynowi barku i działającej siły, czyli:
M = l * F.
Biorąc pod uwagę tę definicję, warunek równowagi dźwigni można przepisać w następujący sposób:
M 1 = M 2 , gdzie M 1 = l 1 * F 1 i M 2 = l 2 * F 2 .
Moment M jest addytywny, co oznacza, że całkowity moment siły dla danego układu można uzyskać przez zwykłe dodanie wszystkich momentów, w których M działa na nim. Należy jednak wziąć pod uwagę ich znak (siła powodująca, że system obraca się przeciwnie do ruchu wskazówek zegara, tworzy dodatni moment + M i na odwrót). W związku z tym reguła momentów dla dźwigni, która jest w równowadze, będzie wyglądać następująco:
Ad
M 1 - M 2 = 0.
Dźwignia traci równowagę, gdy M 1 ≠ M 2 .
Gdzie jest stosowana zasada dźwigni?
Przytoczyliśmy już kilka przykładów użycia tego prostego i dobrze znanego mechanizmu od czasów starożytnych. Oto kilka dodatkowych przykładów:
- Szczypce: dźwignia pierwszego rodzaju, która pozwala na tworzenie ogromnych wysiłków ze względu na niewielką długość ramion l 2, gdzie znajdują się zęby narzędziowe.
- Otwieracz wieka puszki i butelki: to dźwignia drugiego rodzaju, więc zawsze daje zysk w wysiłku.
- Wędka: dźwignia trzeciego rodzaju, która pozwala na przesunięcie końca wędki za pomocą pływaka, ciężarka i haka o dużych amplitudach. Utrata w tym przypadku jest odczuwalna, gdy rybak ma trudności z wyłowieniem ryby, nawet jeśli jej waga nie przekracza 0,5 kg.

Sam człowiek ze stawami, mięśniami, kośćmi i ścięgnami jest żywym przykładem systemu z wieloma różnymi dźwigniami.
Rozwiązywanie problemów
Stan równowagi dźwigni omawiany w artykule służy do rozwiązania prostego problemu. Konieczne jest obliczenie przybliżonej długości ramienia dźwigni, przyłożenie wysiłku do końca, Archimedes był w stanie podnieść statek, jak opisuje to Plutarch.

Aby rozwiązać, wprowadzamy następujące założenia: weźmy pod uwagę grecką trirealność 90 ton z przesunięciem i zakładamy, że wsparcie dźwigni wynosi 1 metr od jej środka masy. Archimedes, zgodnie z legendą, mógł z łatwością podnieść statek, wtedy założymy, że w tym celu przyłożył siłę równą połowie jego ciężaru, czyli około 400 N (dla masy 82 kg). Następnie, stosując stan równowagi dźwigni, uzyskujemy:
F 1 * l 1 = F 2 * l 2 => l 1 = F 2 * l 2 / F 1 = m * g * l 2 / F 1 = 90000 * 9,81 * 1/400 ≈ 2,2 km.
Nawet jeśli zwiększymy siłę stosowaną do wartości masy Archimedesa i przyniesiemy wsparcie jeszcze dwa razy, wówczas długość ramion będzie wynosić około 500 metrów, co również jest dużą wartością. Najprawdopodobniej legenda o Plutarchie jest przesadą dla wykazania skuteczności dźwigni, a Archimedes nie podniósł statku ponad wodę.