Znajdź obwód trójkąta na różne sposoby.
Obwód każdego trójkąta jest długością linii ograniczającej kształt. Aby to obliczyć, musisz znać sumę wszystkich boków tego wielokąta.
Obliczanie z tych długości boków
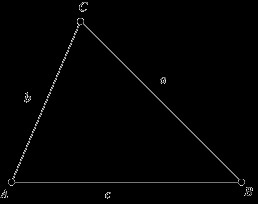
Kiedy ich znaczenie jest znane, jest to łatwe. Oznaczając te parametry literami m, n, k i obwodem literą P, otrzymujemy wzór do obliczenia: P = m + n + k. Zadanie: Wiadomo, że trójkąt ma boki o długości 13,5 decymetra, 12,1 decymetra i 4,2 decymetra. Znajdź obwód. Rozwiązujemy: Jeżeli boki danego wielokąta wynoszą a = 13,5 dm, b = 12,1 dm, c = 4,2 dm, to P = 29,8 dm. Odpowiedź: P = 29,8 dm.
Obwód trójkąta, który ma dwie równe strony
Taki trójkąt nazywa się równoramienicą. Jeśli te równe strony mają długość jednego centymetra, a trzecia strona ma b centymetry długości, to obwód jest łatwy do rozpoznania: P = b + 2a. Zadanie: trójkąt ma dwie strony po 10 decymetrów, podstawę 12 decymetrów. Znajdź P. Rozwiązanie: Niech strona a = c = 10 dm, podstawa b = 12 dm. Suma boków wynosi P = 10 dm + 12 dm + 10 dm = 32 dm. Odpowiedź: P = 32 decymetry.
Obwód trójkąta równobocznego

Jeśli wszystkie trzy strony trójkąta mają taką samą liczbę jednostek, nazywa się je równobocznymi. Inne imię jest poprawne. Obwód zwykłego trójkąta można znaleźć za pomocą wzoru: P = a + a + a = 3 · a. Zadanie: Mamy równoboczny trójkątny działkę. Jedna strona ma 6 metrów. Znajdź długość ogrodzenia, które może zamknąć ten obszar. Rozwiązanie: Jeśli bok tego wielokąta wynosi a = 6m, to długość ogrodzenia wynosi P = 3 · 6 = 18 (m). Odpowiedź: P = 18 m.
Trójkąt o kącie 90 °
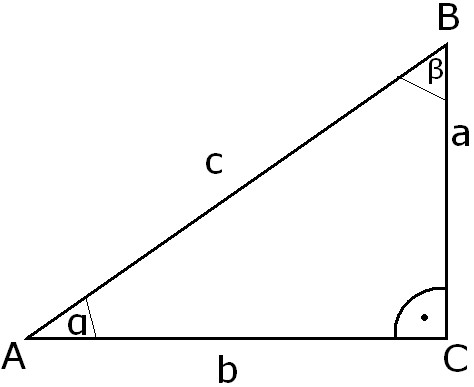
Nazywa się prostokątny. Obecność kąta prostego umożliwia znalezienie nieznanych boków przy użyciu definicji funkcji trygonometrycznych i twierdzenia Pitagorasa. Najdłuższy bok nazywa się przeciwprostokątną i jest oznaczony przez c. Istnieją dwa kolejne boki, aib. Idąc za twierdzeniem noszącym nazwę Pitagorasa, mamy c 2 = a 2 + b 2 . Nogi to a = √ (c 2 - b 2 ) i b = √ (c 2 - a 2 ). Znając długość dwóch odnóg aib, obliczamy przeciwprostokątną. Następnie znajdujemy sumę boków rysunku, dodając te wartości. Zadanie: Cateta trójkąt prostokątny mają długość 8,3 centymetra i 6,2 centymetra. Obwód trójkąta musi być obliczony. Rozwiązujemy: Oznaczamy nogi a = 8,3 cm, b = 6,2 cm Zgodnie z twierdzeniem Pitagorasa, przeciwprostokątna wynosi c = √ (8,3 2 + 6.2 2 ) = √ (68,89 + 38,44) = √ 107 33 = 10,4 (cm). P = 24,9 (cm). Lub P = 8,3 + 6,2 + √ (8,3 2 + 6,2 2 ) = 24,9 (cm). Odpowiedź: P = 24,9 cm, wartości korzeni zabrano do dziesiątej. Jeśli znamy wartości przeciwprostokątnej i nogi, to wartość P otrzymamy obliczając P = √ (c 2 - b 2 ) + b + c. Zadanie 2: Działka, która leży naprzeciwko kąta 90 stopni, 12 km, jedna z nóg to 8 km. Ile czasu możesz przebyć w okolicy, jeśli poruszasz się z prędkością 4 kilometrów na godzinę? Rozwiązanie: jeżeli największy segment ma 12 km, mniej niż b = 8 km, wówczas długość całej ścieżki będzie wynosić P = 8 + 12 + √ (12 2 - 8 2 ) = 20 + √80 = 20 + 8,9 = 28,9 ( km). Znajdziemy czas, dzieląc ścieżkę przez prędkość. 28,9: 4 = 7,255 (h). Odpowiedź: możesz poruszać się przez 7,3 godziny kwadratowe korzenie a odpowiedź zajmujemy do dziesiątej. Możesz znaleźć sumę boków trójkąta prostokątnego, jeśli jedna z boków jest podana, a wartość jednego z ostrych rogów. Znając długość nogi b i wartość przeciwnego kąta β, znajdujemy nieznaną stronę a = b / tg β. Znajdź przeciwprostokątną c = a: sinα. Obwód takiej liczby znajduje się poprzez dodanie uzyskanych wartości. P = a + a / sinα + a / tg α, lub P = a (1 / sin α + 1 + 1 / tg α). Zadanie: W prostokącie Δ АВС z kątem prostym C, nogi słońca mają 10 m długości, a kąt A wynosi 29 stopni. Konieczne jest znalezienie sumy stron Δ АВС. Rozwiązanie: Mamy na myśli znaną nogę BC = a = 10 m, kąt leżący naprzeciwko niej, ∟А = α = 30 °, następnie noga AC = b = 10: 0,58 = 17,2 (m), przeciwprostokątna AB = c = 10: 0,5 = 20 (m). P = 10 + 17,2 + 20 = 47,2 (m). Lub P = 10 · (1 + 1,72 + 2) = 47,2 m. Mamy: P = 47,2 m. Przyjmujemy wartość funkcji trygonometrycznych z dokładnością do jednej setnej, długość boków i obwód są zaokrąglane do dziesiątej. Mając wartość nogi α i sąsiedniego kąta β, dowiadujemy się, czym jest druga noga: b = tan β. Przeciwprostokątna w tym przypadku będzie równa nodze podzielonej przez cosinus kąta β. Obwód znany jest ze wzoru P = a + a tg β + a: cos β = (tg β + 1 + 1: cos β) · a. Zadanie: Noga trójkąta o kącie 90 stopni 18 cm, kąt sąsiedni wynosi 40 stopni. Znajdź P. Rozwiązanie: Oznaczamy znaną nogę BC = 18 cm, ∟β = 40 °. Następnie nieznana noga AC = b = 18 · 0,83 = 14,9 (cm), przeciwprostokątna AB = c = 18: 0,77 = 23,4 (cm). Suma boków rysunku jest równa = 56,3 (cm). Lub P = (1 + 1,3 + 0,83) * 18 = 56,3 cm Odpowiedź: P = 56,3 cm Jeśli długość przeciwprostokątnej c i dowolnego kąta α jest znana, nogi będą równe iloczynowi przeciwprostokątnej dla pierwszy - na grzbiecie i na drugim - na cosinusie tego kąta. Obwód tej figury to P = (sin α + 1 + cos α) * c. Zadanie: Hipotencjaza trójkąta prostokątnego AB = 9,1 centymetra i kąt 50 stopni. Znajdź sumę boków tej figury. Rozwiązanie: Określmy przeciwprostokątną: AB = c = 9,1 cm, ∟A = α = 50 °, a następnie jedna z nóg BC ma długość a = 9,1 · 0,77 = 7 (cm), ACH = b = 9 , 1 · 0,64 = 5,8 (cm). Zatem obwód tego wielokąta wynosi P = 9,1 + 7 + 5,8 = 21,9 (cm). Lub P = 9,1 · (1 + 0,77 + 0,64) = 21,9 (cm). Odpowiedź: P = 21,9 centymetra.
Arbitralny trójkąt, którego jedna strona jest nieznana
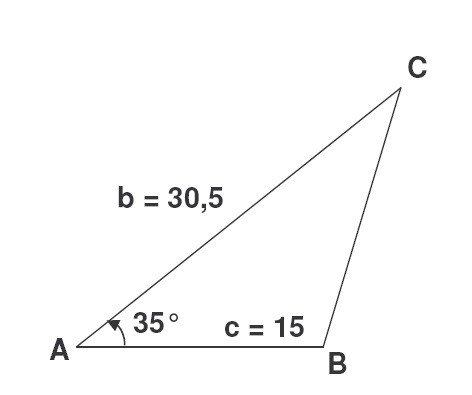
Jeśli mamy wartości dwóch boków a i c, a kąt między tymi bokami wynosi γ, to znajdujemy trzecie twierdzenie cosinusów: b 2 = с 2 + a 2 - 2 i cos β, gdzie β jest kątem między bokami a i c. Następnie znajdujemy obwód. Zadanie: Δ АВС ma odcinek AB o długości 15 dm, odcinek AU, którego długość wynosi 30,5 dm. Kąt między tymi bokami wynosi 35 stopni. Oblicz sumę stron Δ ABC. Rozwiązanie: Twierdzenie Cosinusa obliczyć długość strony trzeciej. BC 2 = 30,5 2 + 15 2 - 2 · 30,5 · 15 · 0,82 = 930,25 + 225 - 750,3 = 404,95. BC = 20,1 cm, P = 30,5 + 15 + 20,1 = 65,6 (dm). Mamy: P = 65,6 dm.
Suma boków dowolnego trójkąta, którego długości dwóch boków są nieznane

Kiedy znamy długość tylko jednego segmentu i wartość dwóch kątów, możemy ustalić długość dwóch nieznanych boków, stosując twierdzenie sinusoidalne: "w trójkącie boki są zawsze proporcjonalne do wartości sinusoidalnych przeciwległych rogów". Gdzie b = (a * sin β) / sin a. Podobnie c = (a sin γ): sin a. Obwód w tym przypadku będzie P = a + (a sin β) / sin a + (a sin γ) / sin a. Zadanie: Mamy Δ ABC. Długość boku BC wynosi 8,5 mm, kąt C 47 °, a kąt B wynosi 35 stopni. Znajdź sumę boków tej figury. Rozwiązanie: oznacz długość boków BC = a = 8,5 mm, AC = b, AB = c, ∟ A = α = 47 °, ∟B = β = 35 °, ∟ C = γ = 180 ° - (47 ° + 35 °) = 180 ° - 82 ° = 98 °. Z relacji wyprowadzonych z twierdzenia sinusowego, znajdziemy nogi AC = b = (8,5 · 0,57): 0,73 = 6,7 (mm), AB = c = (7 · 0,99): 0,73 = 9,5 (mm). W związku z tym suma boków tego wielokąta wynosi P = 8,5 mm + 5,5 mm + 9,5 mm = 23,5 mm. Odpowiedź: P = 23,5 mm. W przypadku, gdy istnieje tylko długość jednego segmentu i wartości dwóch sąsiednich kątów, najpierw obliczamy kąt przeciwny do znanej strony. Wszystkie rogi tej figury mają w sumie 180 stopni. Dlatego ∟A = 180 ° - (∟B + ∟C). Następnie odnajdujemy nieznane segmenty z wykorzystaniem twierdzenia sinusoidalnego. Zadanie: Mamy Δ ABC. Ma odcinek BC równy 10 cm, kąt B wynosi 48 stopni, kąt C wynosi 56 stopni. Znajdź sumę stron Δ abc. Rozwiązanie: Najpierw znajdź wartość kąta A, po przeciwnej stronie BC. ∟A = 180 ° - (48 ° + 56 °) = 76 °. Teraz za pomocą twierdzenia o sinusie, obliczyć długość boku AC = 10 · 0,74: 0,97 = 7,6 (cm). AB = BC * sin C / sin A = 8,6. Obwód trójkąta to P = 10 + 8,6 + 7,6 = 26,2 (cm). Wynik: P = 26,2 cm.
Obliczanie obwodu trójkąta za pomocą promienia wpisanego w niego okręgu
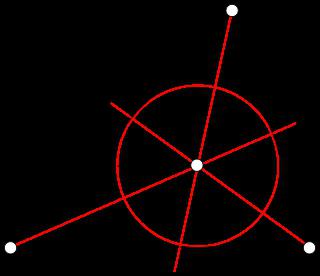
Czasami nie jest znane żadne z warunków problemu. Ale jest wartość obszar trójkąta i promień wpisanego koła. Te wartości są powiązane: S = r p. Znając wartość obszaru trójkąta, promień r, możemy znaleźć pół-obwód p. Znajdź p = S: r. Zadanie: Działka ma powierzchnię 24 m 2 , promień r wynosi 3 m. Znajdź liczbę drzew, które powinny być sadzone równomiernie wzdłuż linii otaczającej tę sekcję, jeśli odległość między dwoma sąsiednimi jest 2 metry. Rozwiązanie: Suma boków tej figury jest następująca: P = 2 · 24: 3 = 16 (m). Następnie podziel przez dwa. 16: 2 = 8. Razem: 8 drzew.
Suma boków trójkąta we współrzędnych kartezjańskich
Wierzchołki Δ АВС mają współrzędne: A (x 1 ; y 1 ), B (x 2 ; y 2 ), C (x 3 ; y 3 ). Znajdź kwadraty z każdej strony AB 2 = (x 1 - x 2 ) 2 + (y 1 - y 2 ) 2 ; BC 2 = (x 2 x 3 ) 2 + (y 2 -y 3 ) 2 ; AC 2 = (x 1 - x 3 ) 2 + (y 1 - y 3 ) 2 . Aby znaleźć obwód, wystarczy dodać wszystkie segmenty. Zadanie: Współrzędne wierzchołków Δ ABC: B (3; 0), A (1; -3), C (2; 5). Znajdź sumę boków tej figury. Rozwiązanie: wprowadzając wartości odpowiednich współrzędnych w formule obwodu, otrzymujemy P = √ (4 + 9) + √ (1 + 25) + √ (1 + 64) = √13 + √26 + √65 = 3,6 + 5,1 +8,0 = 16,6. Mamy: P = 16,6. Jeśli figurka nie znajduje się na płaszczyźnie, ale w przestrzeni, wówczas każdy z wierzchołków ma trzy współrzędne. W związku z tym suma stron będzie miała jeszcze jeden termin.
Metoda wektorowa
Jeśli kształt jest określony przez współrzędne wierzchołków, obwód można obliczyć za pomocą metody wektorowej. Wektor jest segmentem mającym kierunek. Jego moduł (długość) jest oznaczony symbolem |||. Odległość między punktami jest długością odpowiedniego wektora lub modułem wektora. Rozważ trójkąt leżący na płaszczyźnie. Jeśli wierzchołki mają współrzędne A (x 1 ; y 1 ), M (x 2 ; y 2 ), T (x 3 ; y 3 ), wówczas długość każdej strony jest określona wzorami: AM = √ ((x 1 - x 2 ) 2 + (y 1 - y 2 ) 2 ), | MT| = √ ((x 2 - x 3 ) 2 + (y 2 - y 3 ) 2 ), | AT = = √ ((x 1 - x 3 ) 2 + ( 1 - 3 ) 2 ). Obwód trójkąta uzyskuje się przez dodanie długości wektorów. Podobnie znajdź sumę boków trójkąta w przestrzeni.