Metoda elementów skończonych i jej zastosowanie

Metoda elementów skończonych stała się jedną z technik badania różnych projektów. Obecnie jest powszechnie uznawany za powszechny sposób rozwiązywania szerokiego zakresu zadań w różnych dziedzinach technologii.

Definicja

Analiza inżynieryjna metodą elementów skończonych polega na przybliżeniu medium ciągłego o nieskończenie dużej liczbie stopni swobody przez zbiór elementów (poddomen) o skończonej liczbie stopni swobody. Wzajemny związek między tymi elementami. Rozpoznanie metody wyjaśniono prostotą jej formy matematycznej i fizycznej interpretacji.

Użyj w mechanice

Metoda elementów skończonych w mechanice pękania i problemach mechaniki strukturalnej wyraża się jako stosunek MES w postaci przemieszczeń. Po pierwsze, tak zwane funkcje formularza są ustawiane w każdym elemencie. Określają ruch w wewnętrznej części elementu przez ruch w węzłach. Te ostatnie to punkty, w których elementy skończone są połączone.

Nieznane FEM są możliwe i niezależne ruchy węzłów modelu elementów skończonych (CEM). W ten sposób projekt KEM jest systemem stałych węzłów. Dodatkowe linki korelują z kierunkiem możliwych ruchów węzłów.

Istota metody

W swej istocie elementarny model konstrukcji jest podobny do podstawowego systemu klasycznej metody przemieszczeń, która jest wykorzystywana przy obliczaniu układów prętów. Aby uzyskać podatną dokładność wyników obliczeń metodą elementów skończonych, konieczne jest zmniejszenie wielkości elementów, zwiększając w ten sposób dokładność przybliżenia cech geometrycznych i funkcji przemieszczeń w elemencie skończonym.

Struktury złożone w CEM osiągają setki lub nawet miliony stopni swobody, a zatem metoda elementów skończonych w inżynierii jest zorientowana maszynowo, której implementacja jest możliwa tylko za pomocą komputerów.

Praktyczne wdrożenie

Aby zastosować MES w praktyce, konieczne jest zrozumienie nie tylko teorii mechaniki, ale także znajomości programowania. Zastosowanie metody elementów skończonych jest często oparte na wariacyjnych zasadach mechaniki, które opierają się na dwóch podstawowych skalarach: potencjale i energia kinetyczna elastyczna konstrukcja. Definicja tych skalarów, niezależnie od wybranego układu współrzędnych, pozwala na wpisanie relacji MES w niezmiennej postaci.

Aby ułatwić programowanie, stosunki FEM są rejestrowane w formie zwartej matrycy lub tensora. Obecnie symulacja metodą elementów skończonych jest w pełni matematycznie uzasadniona, powstają produkty o wysokiej wydajności, które są stale ulepszane wraz z narzędziami programistycznymi.

Programy edukacyjne

Postęp techniczny, szczególnie w dziedzinie komputerów, znacząco zmienił poglądy na temat formułowania i rozwiązywania problemów inżynierskich. Budowa modelu obliczeniowego jest ściśle powiązana z procesem obliczeniowym i prawie niemożliwe jest rozdzielenie tych dwóch etapów na ścieżkę uzyskiwania praktycznych rezultatów.

Metoda elementów skończonych jest szeroko stosowana w praktyce inżynierskiej, co również przyczyniło się do jej włączenia do programów nauczania uniwersytetów. MES umożliwia budowanie matematycznego modelu rozważanego zjawiska w oparciu o jego fizyczną istotę.

Pierwsze podręczniki na temat MES zostały napisane w skomplikowanym języku, ale wkrótce metody nauczania zostały uproszczone dzięki wprowadzeniu specjalistycznych programów. Na przykład pakiet oprogramowania Assistant sprawdzi się dobrze. Umożliwia on testowanie wiedzy uczniów w trybie online i przyczynia się do rozwoju umiejętności pracy z oprogramowaniem w rozwiązywaniu praktycznych problemów.

Obliczanie deformacji liniowych

Dzisiaj podstawy metody elementów skończonych opierają się na tym, że wartości i pojęcia w niej zawarte nie są z góry wprowadzane, ale wynikają z istoty problemu mechaniki strukturalnej. Zakres problemów, które można rozwiązać za pomocą FEM jest prawie nieograniczony. Rozważmy na przykład problem obliczenia liniowej deformacji struktur sprężystych z działania obciążeń statycznych.

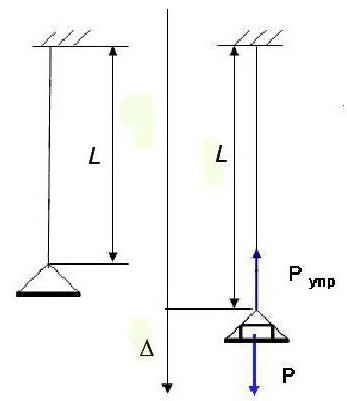
Angielski fizyk R. Hooke przeprowadził badania odkształceń prętów obciążonych centralnie wykonanych z różnych materiałów sprężystych pod działaniem siły statycznej: Δ = Pl / EA.

Ustalił także zależność między ilościami, które określają ten proces: σ = Eε, gdzie deformacja jest wyrażona przez relację ε = Δ / l, naprężenie jest oznaczone jako σ = P / A (tutaj A jest przekrojem poprzecznym pręta).

Współczynnik proporcjonalności E określa właściwości sprężyste materiału i ma istotę fizyczną - naprężenie odpowiadające naprężeniu jednostkowemu.

Wpływ siły statycznej

Statycznie działająca siła rośnie stopniowo wraz z upływem czasu (G≥P≥0). Ruchy, które generuje, rosną również stopniowo, bez przyspieszenia.

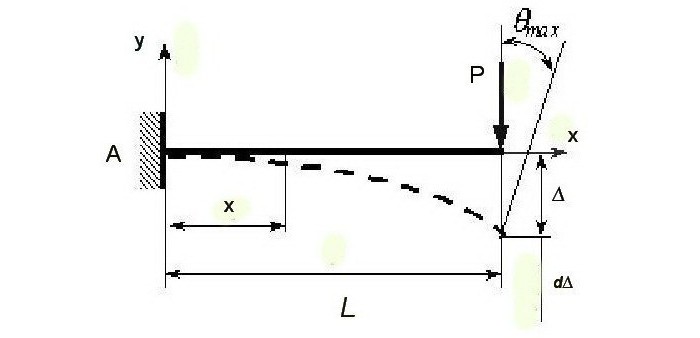
Analiza metodą elementów skończonych pozwala nam określić wpływ siły statycznej na przemieszczenie, biorąc pod uwagę, że te wskaźniki są różne. Zwiększenie (wzrost) w życie na nieskończenie małej wartości dP odpowiada wzrostowi (wzrostowi) w przesunięciu dΔ. Siła robocza (P + ΔP) przy przemieszczeniu dΔ wynosi dA = (P + ΔP) × dΔ.

Ostateczna wartość siły roboczej jest określona wzorem A = PdΔ.

Wprowadźmy zależność między zmiennymi wymiarowymi pod znakiem całki Δ = Pα, gdzie α jest współczynnikiem zgodności, który wyraża fizyczną istotę ruchu punktu, do którego dodaje się jednostkę, w kierunku tej siły. Współczynnik Δ = Pα ustawia jednostkę miary α (m / N). Wynika z tego, że dΔ = dPα.

Współczynnik zgodności odpowiada innej ważnej charakterystyce konstrukcji - współczynnikowi sztywności k = l / α (n / m), który określa siłę powodującą pojedynczy ruch konstrukcji w kierunku tej siły.

Biorąc pod uwagę wszystkie cechy i współczynniki, końcowe równanie przyjmuje postać: A = PdPα = α × (P 2/2) = (GΔ) / 2.

Otrzymano wzór Clapeyrona, który określa rzeczywistą pracę siły działającej statycznie na przemieszczenie, która sama wytworzyła się w elastycznym ciele. Inne metody numeryczne są obliczane przy użyciu tej techniki.

Metoda elementów skończonych dla systemów prętowych

Wędka jest przestrzennym ciałem, którego dwa rozmiary, szerokość i wysokość, są znacznie mniejsze niż długość. Pozwala to na rozważenie jego fizycznego modelu w postaci linii przechodzącej przez centra przekrojów. Jeśli siły zewnętrzne przyłożone do pręta znajdują się w tej samej płaszczyźnie co jego model, wówczas możemy przyjąć, że jego odkształcenia występują w tej samej płaszczyźnie.

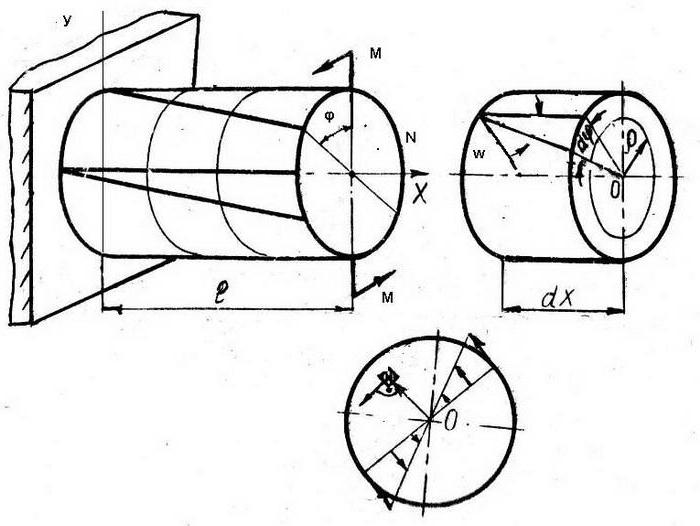
Z matematycznego punktu widzenia geometryczne cechy przemieszczenia i naprężenia w pręcie są funkcjami tego samego argumentu. Relacje teorii elastyczności opierają się na hipotezie płaskich odcinków pręta. Zależność między odkształceniami i naprężeniami odpowiada liniowemu prawu Hooke'a. W każdej części pręta pojawiają się trzy płaszczyzny ruchu:

• współrzędna u jest siłą wzdłużną;
• współrzędna w - odchylenie;
• współrzędna φ - kąt obrotu.

W tym przypadku podłużne u i odchylenie w są niezależne, a kąt obrotu jest wyrażony wzorem φ = dw / dx, gdzie dw jest wielkością ugięcia po przyłożeniu siły zewnętrznej do pręta, dx jest segmentem odchylania (określonym przez wartość w + dw).

Dla nieskończenie małego pręta dx ważna jest zależność dx = dφ × P.

Potencjał energii Deformacje prętów są naturalnie obliczane w lokalnym układzie współrzędnych, którego oś x pokrywa się z osią pręta, a oś y jest prostopadła do osi pręta: U = ½∫N × du + ½∫ M × dφ = ½∫N × (du / dx) dx + ½ ∫M × (d²w / dx²) dx.

Podejście izoparametryczne w MES

Rozważ zastosowanie metody elementów skończonych w izoparametrycznym systemie elementów skończonych konstrukcji płaskiej. Proces tworzenia modelu elementów skończonych składa się z kilku etapów, z których pierwszym jest budowa siatki elementów skończonych (FE), wybór globalnego układu współrzędnych w odniesieniu do całej struktury i systemu lokalnego związanego z elementem skończonym.

Kluczowym krokiem jest zdefiniowanie funkcji formularza, które zapewniają definicję przemieszczeń w elemencie skończonym w związku z ruchem jego węzłów. Istnieją różne sposoby konstruowania funkcji formy, ale muszą one zapewniać spełnienie szeregu warunków przybliżających funkcje przemieszczeń.

• Spełnienie ciągłości przemieszczeń nie tylko w węzłach elementów skończonych, ale także na ich granicach.
• Zapewnienie zachowania pochodnych funkcji wypierania, które są związane z potencjałem sprężystym.
• Ruch elementu skończonego jako sztywnej liczby całkowitej. Oznacza to, że gdy element jest przemieszczany jako bryła, składowe wektora deformacji są zerowe.

Problemy i rozwiązania

Teoria metod elementów skończonych stwierdza, że ​​relacje MES powstają w lokalnym układzie współrzędnych. Dlatego wymienione wymagania dla funkcji formularza są wykonywane automatycznie, jeśli osie układu lokalnego są zorientowane wzdłuż boków elementu skończonego. Takie przypadki mają miejsce w przypadku elementów skończonych konstrukcji rdzeniowych, prostokątnych paneli ściennych i prostokątnych płyt.

Ale w praktyce istnieją konstrukcje o zarysie arbitralnej definicji. W tym przypadku konieczne jest przeprowadzenie transformacji w celu przybliżenia przemieszczeń w globalnym układzie współrzędnych, co prowadzi do nieciągłości przemieszczeń na granicach elementów skończonych, aw rezultacie do utraty dokładności obliczeń przybliżonych.

Powstał pomysł pokazania płaskiego, czworokątnego skończonego elementu o ogólnej formie na kwadracie z lokalnym układem współrzędnych, którego początek znajduje się w środku tej figury, a osie zorientowane po bokach. W celu dalszego wykorzystania elementów skończonych w postaci kwadratu, konieczne jest ustanowienie połączenia jeden-do-jednego pomiędzy lokalnymi współrzędnymi dowolnego czworobocznego FE a lokalnym układem współrzędnych FE w postaci kwadratu. Rzeczywiście, dla kwadratowego elementu skończonego, funkcje formularza są skonstruowane raczej prosto.

Metoda elementów skończonych do obliczeń płyt

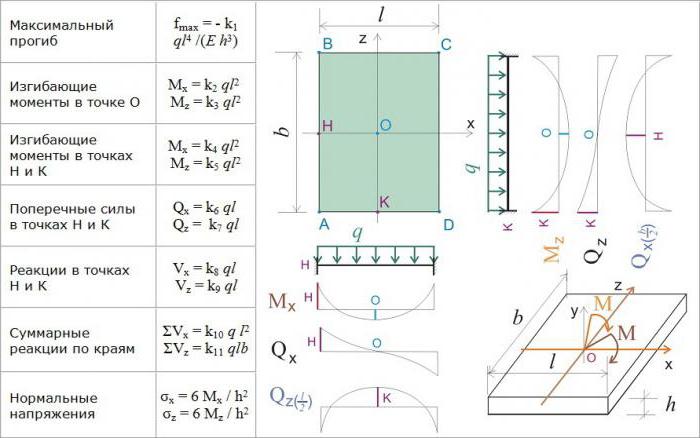
Płyta jest wkładką lub cylindrycznym korpusem, którego wysokość jest znacznie mniejsza niż rozmiar w planie. Wymiar wysokości nazywa się grubością blachy. Płaszczyzna dzieląca wysokość płyty na pół nazywa się płaszczyzną środkową lub referencyjną. Linia przecięcia powierzchni bocznej z płaszczyzną środkową nazywana jest konturem płyty.

Uważa się, że cienka płytka, dla której stosunek grubości do mniejszego wymiaru w planie jest w granicach h≤L / 5, gdzie h jest grubością płyty, L jest jej szerokością.

Płyta jest uważana za sztywną, jeżeli pod wpływem poprzecznego obciążenia jej największe ugięcie podczas deformacji nie przekracza 1/5 jej grubości.

Przy obliczaniu metodą FE najpierw wprowadza się układ współrzędnych: X ₁ , X ₂ i X ₃ . Początek osi X ₁ i X ₂ znajduje się w płaszczyźnie środkowej. Oś X _{3 jest} zorientowana wzdłuż normalnej do płaszczyzny środkowej.

Obliczenia są zwykle redukowane do obliczania przemieszczenia (przesunięcia) płyty w pewnym punkcie pod wpływem obciążeń (sił). W dowolnym punkcie płytki, która jest uważana za ciało trójwymiarowe, pojawiają się trzy kierunki ruchu: U ₁ , U ₂ , U ₃ . Definicja to ruch wzdłuż linii normalnej do płaszczyzny środkowej, nazywanej ugięciem i oznaczony literą W.

Obliczenia uważa się za wykonane, jeżeli z danego obciążenia (i jest to zwykle równomiernie rozłożone, skierowane na powierzchnię), ustala się metodę obliczania przemieszczeń U i przesunięcia W w dowolnym punkcie płytki. Relacje MES oparte są na założeniach technicznej teorii sprężystości zaproponowanej przez fizyka Kirchhoffa.

Hipotezy Kirchhoffa

Metoda elementów skończonych jest w dużej mierze oparta na hipotezach sformułowanych w 1845 r. Przez niemieckiego fizyka G. Kirghoff. Bezpośrednia normalna hipoteza stwierdza, że ​​jakakolwiek linia prostoliniowa normalna do płaszczyzny środkowej nieodkształconej płyty pozostaje prosta i normalna do środkowej powierzchni odkształconej płytki, a długość linii prostej nie zmienia się. Jego istota polega na braku przesunięcia między warstwami płyty o grubości.

Jeśli osie współrzędnych kartezjańskich są umieszczone w taki sposób, że płaszczyzny X ₁ , X ₂ pokrywają się z płaszczyzną środkową, to z pierwszej części hipotezy wynikają następujące równania: y ₁₃ = 0, y ₂₃ = 0. Hipoteza o niezmienności długości linii prostej zakłada, że ​​liniowe odkształcenie w kierunku osi _X3 wynosi zero: ε ₃₃ = 0.

Hipoteza o braku ciśnienia między warstwami płyty równoległą do środkowej powierzchni sugeruje, że naprężenia σ _{33 w} porównaniu do naprężeń σ ₁₁ i σ ₂₂ można pominąć, to znaczy σ ₃₃ = 0.

Hipoteza nieodkształcalności płaszczyzny środkowej sugeruje, że w środkowej płaszczyźnie płyty nie ma deformacji naprężenia, ściskania i ścinania. Oznacza to, że płaszczyzna środkowa jest neutralna. Więc w tym przemieszczeniu U ₁ = U2 = 0.

Wniosek

Metoda elementów skończonych, która jest szeroko stosowana w konstrukcjach i mechanice, pozwala obliczyć przemieszczenia różnych elementów poddanych pewnym obciążeniom. System, sformułowany w 1936 roku przez radzieckich naukowców, zaczął być szeroko stosowany dopiero kilkadziesiąt lat później, ponieważ wymagał dużej ilości obliczeń. Wraz z wprowadzeniem komputerów zadanie to jest uproszczone.