Jak znaleźć liczby pierwsze?

Liczby są różne: naturalny, naturalny, racjonalny, całkowity i ułamkowy, pozytywny i negatywny, złożony i prosty, nieparzysty i parzysty, prawdziwy itd. Z tego artykułu dowiesz się, jakie są proste liczby.

Jakie liczby są nazywane angielskim słowem "simpl"?

Bardzo często, uczniowie na jednym z najbardziej nieskomplikowanych na pierwszy rzut oka pytań z matematyki, na temat tego, jaka jest pierwsza liczba, nie wiedzą, jak odpowiedzieć. Często mylą proste liczby z liczbami naturalnymi (to jest liczbami, których używają ludzie podczas liczenia przedmiotów, podczas gdy w niektórych źródłach zaczynają od zera, aw innych - od jednego). Ale to są zupełnie dwie różne rzeczy. Liczby pierwsze są naturalne, to znaczy liczby całkowite i liczby dodatnie, które są większe niż jeden i które mają tylko 2 naturalne dzielniki. W tym przypadku jeden z tych dzielników jest podaną liczbą, a drugi jest jedną. Na przykład trzy to liczba pierwsza, ponieważ nie jest ona podzielna przez żaden inny numer oprócz siebie i jednego.

Numery złożone

Przeciwieństwem liczb pierwszych jest złożony. Są również naturalne, także więcej niż jeden, ale nie mają dwóch, ale większą liczbę dzielników. Na przykład liczby 4, 6, 8, 9 itp. Są liczbami naturalnymi, złożonymi, ale nie liczbami pierwszymi. Jak widać, są to w większości parzyste liczby, ale nie wszystkie. Ale "dwa" - parzysty numer i "pierwszy numer" w serii liczb pierwszych.

Sekwencja

Aby zbudować szereg liczb pierwszych, konieczne jest dokonanie selekcji ze wszystkich liczb naturalnych, biorąc pod uwagę ich definicję, czyli należy działać odwrotnie. Konieczne jest rozważenie każdej z dodatnich liczb całkowitych, aby określić, czy ma więcej niż dwie przegrody. Spróbujmy zbudować serię (sekwencję) składającą się z liczb pierwszych. Lista zaczyna się od dwóch, kolejne trzy, ponieważ dzieli się tylko na siebie i na jednostki. Weź pod uwagę numer cztery. Czy ma dzielniki oprócz czterech i jednego? Tak, ta liczba to 2. Zatem cztery nie są liczbą pierwszą. Pięć jest również proste (nie jest podzielne przez żadną inną liczbę oprócz 1 i 5), ale sześć jest podzielnych. Generalnie, jeśli podążysz za wszystkimi liczbami parzystymi, zobaczysz, że z wyjątkiem "dwóch", żadna z nich nie jest prosta. Stąd dochodzimy do wniosku, że liczby parzyste, z wyjątkiem dwóch, nie są proste. Kolejne odkrycie: wszystkie liczby podzielne na trzy, z wyjątkiem samej triady, czy to parzystej czy nieparzystej, również nie są proste (6, 9, 12, 15, 18, 21, 24, 27 itd.). To samo dotyczy liczb podzielonych na pięć i siedem. Wszystkie z nich również nie są proste. Podsumujmy. A więc pojedyncze cyfry to wszystko liczby nieparzyste z wyjątkiem jednego i dziewięciu, a nawet parzystych "tylko dwóch". Dziesiątki samych siebie (10, 20, ... 40 itd.) Nie są proste. Dwucyfrowe, trzycyfrowe itd. Proste liczby można określić na podstawie zasad opisanych powyżej: jeśli nie mają innych dzielników innych niż one i one.

Teorie dotyczące właściwości liczb pierwszych

Istnieje nauka, która bada właściwości liczb całkowitych, w tym liczb pierwszych. Jest to gałąź matematyki, którą nazywa się najwyższą. Oprócz właściwości liczb całkowitych zajmuje się również liczbami algebraicznymi, transcendentalnymi, a także funkcjami o różnym pochodzeniu związanymi z arytmetyką tych liczb. W badaniach tych oprócz metod elementarnych i algebraicznych stosuje się również metody analityczne i geometryczne. W szczególności, badanie liczb pierwszych zaangażowanych w teorii liczb.

Liczby pierwsze są "cegiełkami" liczb naturalnych.

W arytmetyce istnieje twierdzenie, które nazywa się głównym. Zgodnie z nią każda liczba naturalna, z wyjątkiem jednej, może być reprezentowana jako produkt, którego współczynniki są liczbami prostymi, a kolejność sekwencji czynników jest unikalna, co oznacza, że ​​sposób reprezentacji jest unikalny. Nazywa się to rozkładem liczby naturalnej na czynniki pierwsze. Jest jeszcze inna nazwa tego procesu - faktoryzacja liczb. Postępując w ten sposób, proste liczby można nazwać "materiałem budowlanym", "blokami" do budowy liczb naturalnych.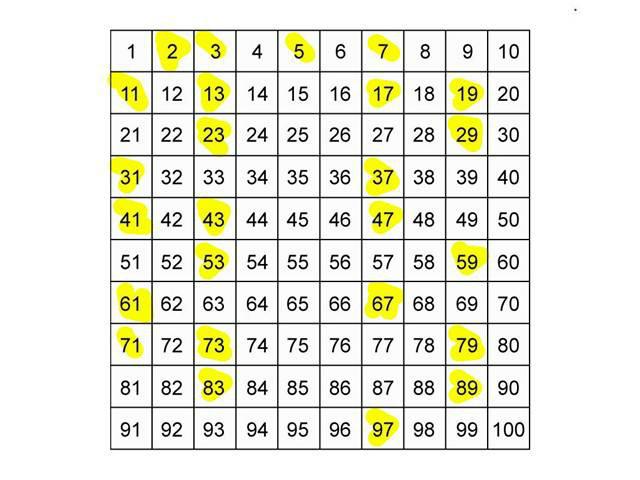

Szukaj liczb pierwszych. Testy prostoty

Wielu uczonych w różnych czasach próbowało znaleźć pewne zasady (systemy) do znalezienia listy liczb pierwszych. Nauka zna systemy, które nazywane są sita Atkin, sito Sundartam i sito Eratostenesa. Jednak nie zapewniają one żadnych znaczących wyników, a do znalezienia liczb pierwszych stosuje się proste sprawdzenie. Również matematycy stworzyli algorytmy. Nazywane są testami prostoty. Na przykład istnieje test opracowany przez Rabin i Miller. Jest używany przez kryptografów. Istnieje również test Kayal-Agraval-Sasken. Jednakże, pomimo wystarczającej dokładności, jest bardzo trudno obliczyć, co pomniejsza jego praktyczną wartość.

Czy zbiór liczb pierwszych ma limit?

Fakt, że zbiór prostych jest nieskończonością, napisał w książce "Zasady" starożytny grecki uczony Euklides. Powiedział to: "Wyobraźmy sobie przez chwilę, że liczby pierwsze mają limit. Następnie pomnóżmy je ze sobą i dodaj jeden do produktu. Liczba uzyskana w wyniku tych prostych działań nie może być podzielona na liczbę liczb pierwszych, ponieważ zawsze pozostanie jedna z nich w pozostałej części. Oznacza to, że istnieje jeszcze inna liczba, która nie została jeszcze uwzględniona na liście liczb pierwszych. Dlatego nasze założenie nie jest prawdziwe, a ten zestaw nie może mieć limitu. Oprócz dowodu Euklidesa, istnieje bardziej nowoczesna formuła podana przez osiemnastowiecznego szwajcarskiego matematyka Leonarda Eulera. Według niego, suma odwrotna do sumy pierwszych n liczb rośnie bez ograniczeń, gdy liczba n rośnie. Ale wzór twierdzenia o rozkładach liczb pierwszych: (n) rośnie jako n / ln (n).

Jaka jest największa liczba pierwsza?

Ten sam Leonard Euler był w stanie znaleźć największy prime na swój czas. To jest 2 ³¹ - 1 = 2147483647. Jednak do 2013 r. Obliczono drugą najdokładniejszą na liście liczb pierwszych, 2 ^57885161 - 1, nazywaną numerem Mersenne. Zawiera około 17 milionów cyfr dziesiętnych. Jak widać, liczba znaleziona przez naukowców z XVIII wieku jest kilkakrotnie mniejsza od tej. Tak właśnie powinno być, ponieważ Euler wykonał te obliczenia ręcznie, a nasz komputer prawdopodobnie pomógł naszym współczesnym. Co więcej, tę liczbę uzyskano na wydziale matematyki na jednym z wydziałów amerykańskich. Liczby, nazwane od tego naukowca, przechodzą test prostoty Luke'a-Lemere'a. Jednak nauka nie chce na tym poprzestać. The Electronic Frontier Foundation, założona w 1990 roku w Stanach Zjednoczonych (EFF), przyznała nagrodę pieniężną za znalezienie dużych liczb pierwszych. A jeśli do 2013 r. Na nagrodę będą polegać ci naukowcy, którzy znajdą ich od 1 do 10 milionów liczb dziesiętnych, dziś ta liczba osiąga od 100 milionów do 1 miliarda. Wielkość nagród waha się od 150 do 250 tysięcy dolarów.

Nazwy specjalnych liczb pierwszych

Liczby, które zostały znalezione dzięki algorytmom stworzonym przez jednego lub drugiego naukowca i przeszły test prostoty, nazywane są specjalnymi. Oto niektóre z nich:

1. Merssen.

2. Wooda.

3. Farma.

4. Cullen.

5. Prota.

6. Mills i in.

Prostotę tych liczb, nazwaną od powyższych naukowców, ustalono, stosując następujące testy:

1. Luc-Lemer.

2. Pepin.

3. Rizel.

4. Billhart - Lemera - Selfridge, itp.

Współczesna nauka nie kończy się na tym i prawdopodobnie w niedalekiej przyszłości świat pozna nazwiska tych, którzy mogą otrzymać nagrodę w wysokości 250 000 $, znajdując największą liczbę pierwszą.