Jak znaleźć wysokość trapezu: wzór na każdą okazję
Istnieje kilka odpowiedzi na proste pytanie "Jak znaleźć wysokość trapezu?", Wszystko dlatego, że można podać różne wartości początkowe. Dlatego formuły będą się różnić.
Te wzory można zapamiętać, ale łatwo można je uzyskać. Trzeba tylko zastosować uprzednio zbadane twierdzenia.
Akceptowane w formułach
We wszystkich poniższych zapisach matematycznych takie odczyty liter są poprawne.
| arbitralne trapez | równoramienny trapez | imię |
| a | a | dolna podstawa |
| w | w | górna podstawa |
| c, d | z | boki |
| n | n | wysokość |
| m | m | środkowa linia |
| d 1 d 2 | d 1 | przekątne |
| s | s | kwadratowy |
| α, β | α | dolne dolne rogi |
| γ, δ | γ, δ | kąty na przecięciu przekątnych |
W danych źródłowych: wszystkie strony
Aby znaleźć wysokość trapezu w ogólnym przypadku, należy użyć następującej formuły:
n = √ (c 2 - (((a - c) 2 + c 2 - d 2 ) / (2 (a - c))) 2 ). Numer 1.
Nie najkrótszy, ale w zadaniach jest dość rzadki. Zwykle możesz korzystać z innych danych.
Formuła, która mówi ci, jak znaleźć wysokość trapezu równoramiennego w tej samej sytuacji, jest znacznie krótsza:
n = √ (c 2 - (a - c) 2/4). Numer 2
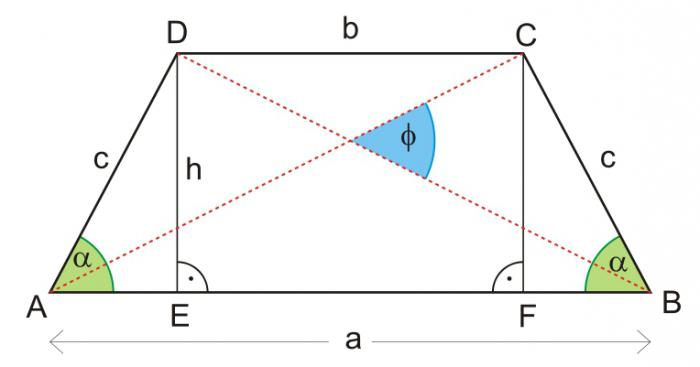
W problemie podane są: boki i kąty w dolnej podstawie
Przyjmuje się, że kąt a przylega do boku z oznaczeniem "c", odpowiednio, kąt β do boku d. Wtedy formuła, jak znaleźć wysokość trapezu, w ogólności będzie:
n = c * sin α = d * sin β. Numer 3
Jeśli liczba jest równoramienna, możesz użyć tej opcji:
n = c * sin α = ((a - c) / 2) * tg α. Numer 4
Znane: przekątne i kąty między nimi
Zazwyczaj dane te są łączone przez wciąż znane wartości. Na przykład linia bazowa lub środkowa. Jeśli podane są powody, to odpowiedź na pytanie, jak znaleźć wysokość trapezu, jest przydatna w następującym wzorze:
n = (d 1 * d 2 * sin γ) / (a + b) lub n = (d 1 * d 2 * sin δ) / (a + b). Numer 5.
Ma to na celu ogólny wygląd postaci. Jeśli podana jest isoscene, rekord zostanie przekształcony w następujący sposób:
n = (d 1 2 * sin γ) / (a + b) lub n = (d 1 2 * sin δ) / (a + b). Numer 6.
Gdy problem dotyczy linii środkowej trapezu, formuły do określenia jego wysokości są następujące:
n = (d 1 * d 2 * sin γ) / 2m lub n = (d 1 * d 2 * sin δ) / 2m. Pokój 5a.
n = (d 1 2 * sin γ) / 2m lub n = (d 1 2 * sin δ) / 2m. Numer 6a.
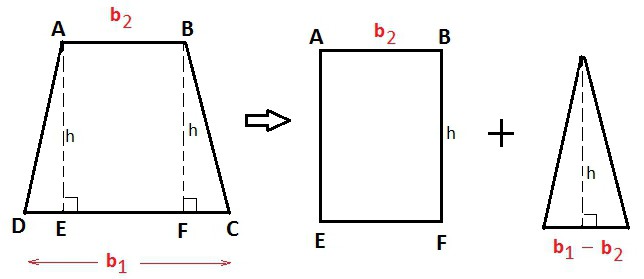
Wśród znanych wartości: powierzchnia z podstawami lub linia środkowa
Są to prawdopodobnie najkrótsze i najprostsze formuły, jak znaleźć wysokość trapezu. Dla dowolnego kształtu będzie to:
n = 2S / (a + c). Numer 7.
To jest to samo, ale z dobrze znaną środkową linią:
n = s / m. Pokój 7a.
Co dziwne, ale w przypadku trapezu równoramiennego formuły będą wyglądały tak samo.
Zadania
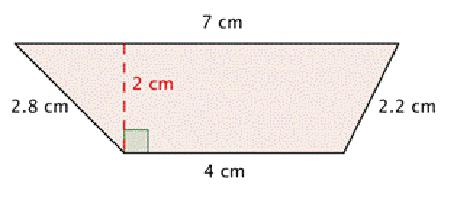
№1. Definicja kątów na dole trapezu.
Stan Podano trapez równoramienny, którego bok ma 5 cm, a jego podstawy mają 6 i 12 cm, aby znaleźć sinus o kącie ostrym.
Decyzja. Dla wygody powinieneś wpisać notację. Niech lewy dolny wierzchołek będzie A, cała reszta zgodnie z ruchem wskazówek zegara: B, C, D. Tak więc dolna podstawa będzie oznaczona PIEKŁA, górna podstawa będzie BC.
Konieczne jest narysowanie wysokości od wierzchołków B i C. Punkty wskazujące końce wysokości będą oznaczone odpowiednio H 1 i H 2 . Ponieważ na rysunku BCH 1 H 2 wszystkie kąty są proste, jest to prostokąt. Oznacza to, że segment H 1 H 2 ma 6 cm.
Teraz musimy wziąć pod uwagę dwa trójkąty. Są równe, ponieważ są prostokątne z identyczną przeciwprostokątną i pionowymi nogami. Wynika z tego, że ich mniejsze nogi są równe. Dlatego można je zdefiniować jako iloraz różnicy. Ta ostatnia jest otrzymywana przez odjęcie od dolnej podstawy górnej. Zostanie podzielony przez 2. Oznacza to, że 12 - 6 należy podzielić przez 2. AN 1 = H 2 D = 3 (cm).
Teraz z twierdzenia Pitagorasa trzeba znaleźć wysokość trapezu. Konieczne jest znalezienie sinusa kąta. BH 1 = √ (5 2 - 3 2 ) = 4 (cm).
Wykorzystując wiedzę o tym, jak sinus kąta ostrego znajduje się w trójkącie prostokątnym, możemy zapisać następujące wyrażenie: sin α = BH 1 / AB = 0,8.
Odpowiedź jest. Pożądany sinus wynosi 0,8.
№2. Aby znaleźć wysokość trapezu przy słynnej stycznej.
Stan W przypadku trapezu równoramiennego musisz obliczyć wysokość. Jego podstawy są znane jako 15 i 28 cm, Dan styczny o kącie ostrym: 11/13.
Decyzja. Oznaczenie wierzchołków jest takie samo, jak w poprzednim zadaniu. Ponownie, musisz trzymać dwie wysokości od górnych rogów. Analogicznie do rozwiązania pierwszego problemu, musisz znaleźć AH 1 = H 2 D, które są zdefiniowane jako różnica 28 i 15 podzielona przez dwa. Po obliczeniach okazuje się, że: 6,5 cm.
Ponieważ styczna jest stosunkiem dwóch odnóg, możemy zapisać następującą równość: tg α = AH 1 / BH 1 . Ponadto stosunek ten wynosi 11/13 (według warunku). Ponieważ AN 1 jest znany, możliwe jest obliczenie wysokości: VN 1 = (11 * 6,5) / 13. Proste obliczenia dają wynik 5,5 cm.
Odpowiedź jest. Wymagana wysokość to 5,5 cm.
№3. Aby obliczyć wysokość znanych przekątnych.
Stan O trapezie wiadomo, że jego przekątne mają 13 i 3 cm, jego wysokość należy znać, jeśli suma podstaw wynosi 14 cm.
Decyzja. Niech oznaczenie tej figury będzie takie samo jak poprzednio. Załóżmy, że głośnik ma mniejszą przekątną. Z wierzchołka C należy utrzymywać żądaną wysokość i oznaczać ją CH.
Teraz musisz wykonać dodatkową konstrukcję. Z kąta C należy narysować linię prostą równoległą do większej przekątnej i znaleźć punkt jej przecięcia z kontynuacją boku ciśnienia krwi. To będzie D 1 . Okazało się to nowym trapezem, wewnątrz którego narysowano trójkąt ASD 1 . Jest również konieczne do dalszego rozwiązania problemu.
Pożądana wysokość będzie również w trójkącie. Dlatego możesz użyć formuł studiowanych w innym temacie. Wysokość trójkąta jest definiowana jako iloczyn liczby 2 i obszaru podzielonego przez stronę, na którą jest narysowany. A strona jest równa sumie podstaw oryginalnego trapezu. Jest to oparte na zasadzie, że wykonano dodatkową konstrukcję.
W rozpatrywanym trójkącie znane są wszystkie strony. Dla wygody wprowadzamy oznaczenie x = 3 cm, y = 13 cm, z = 14 cm.
Teraz możesz policzyć obszar, używając twierdzenia Gerony. Półprzestrzeń będzie wynosić p = (x + y + z) / 2 = (3 + 13 + 14) / 2 = 15 (cm). Formuła dla obszaru po zamianie wartości będzie wyglądać następująco: S = √ (15 * (15 - 3) * (15 - 13) * (15 - 14)) = 6 √10 (cm 2 ).
Teraz musisz policzyć wysokość: n = (2 * 6 √10) / 14 = 6√10 / 7 (cm).
Odpowiedź jest. Wysokość to 6 × 10/7 cm.
№4. Aby wyszukać wysokości po bokach.
Stan Podany jest trapez, którego trzy boki mają 10 cm, a czwarte 24 cm, trzeba znać jego wysokość.
Decyzja. Ponieważ liczba jest równoramienna, będziesz potrzebował formuły numer 2. W niej wystarczy podstawić wszystkie wartości i policzyć. Będzie wyglądać tak:
n = √ (10 2 - (10 - 24) 2/4) = √51 (cm).
Odpowiedź jest. n = √51 cm