Jak znaleźć sinus kąta

Sinus jest jedną z podstawowych funkcji trygonometrycznych, której użycie nie ogranicza się tylko do geometrii. Tabele do obliczania funkcji trygonometrycznych, a także kalkulatory inżynierskie, nie zawsze są dostępne, a czasami obliczanie sinusa jest potrzebne do rozwiązywania różnych problemów. Generalnie, obliczanie sinusoidy pomoże utrwalić umiejętności redagowania i znajomość tożsamości trygonometrycznych.

Gry z linijką i ołówkiem

Proste zadanie: jak znaleźć sinus kąta narysowanego na papierze? Będziesz potrzebował standardowej linijki, trójkąta (lub kompasu) i ołówka. Najprostszym sposobem obliczenia sinusa kąta może być podzielenie skrajnej odnogi trójkąta pod kątem prostym na dłuższym boku - przeciwprostokątna. W związku z tym najpierw trzeba dodać ostrą kąt do figury. trójkąt prostokątny rysowanie linii prostopadłej do jednego z promieni w dowolnej odległości od wierzchołka narożnika. Konieczne będzie utrzymywanie kąta dokładnie 90 °, do czego będziemy potrzebować trójkąta piśmiennego.

Używanie kompasu jest trochę bardziej dokładne, ale trwa dłużej. Na jednej z belek musisz zaznaczyć 2 punkty w pewnej odległości, ustawić promień w przybliżeniu równy odległości między punktami na kompasie i narysować półokrągi z punktami w tych punktach, aż do uzyskania przecięć tych linii. Łącząc punkty przecięcia naszych okręgów ze sobą, uzyskujemy ścisłą prostopadłość do promienia naszego kąta, pozostaje tylko poszerzyć linię do przecięcia z innym promieniem.

W wynikowym trójkącie należy zmierzyć linijką stronę przeciwną do kąta i długą stronę na jednym z promieni. Stosunek pierwszego pomiaru do drugiego i będzie pożądaną wartością sinusa kąta ostrego.

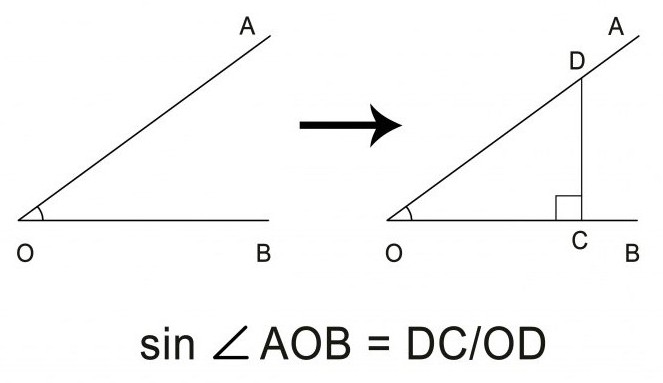
Znajdź sinus dla kąta większego niż 90 °

W przypadku tępego kąta zadanie nie jest trudniejsze. Konieczne jest narysowanie promienia z wierzchołka w przeciwnym kierunku za pomocą linijki, aby utworzyć linię prostą z jednym z promieni kąta zainteresowania. W związku z tym, że uzyskany kąt ostry powinien być wykonany jak opisano powyżej, sinusy sąsiednich kątów, tworzących razem kąt rozwarcia 180 °, są równe.

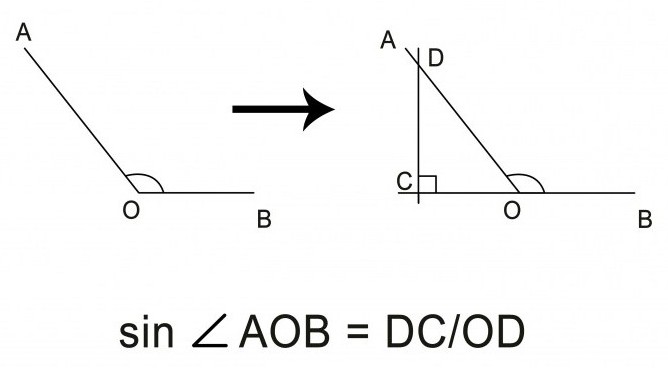
Obliczanie sinusa dla innych funkcji trygonometrycznych

Obliczenie sinusoidalne jest również możliwe, jeśli znane są wartości innych funkcji trygonometrycznych kąta lub przynajmniej długości boków trójkąta. Pomoże nam to w identyfikacji trygonometrycznej. Przeanalizujmy typowe przykłady.

Jak znaleźć sinus w znanej cosinusie kąta? Pierwsza tożsamość trygonometryczna, wyprowadzona z twierdzenia Pitagorasa, stwierdza, że ​​suma kwadratów sinusa i cosinusa o tym samym kącie jest równa jeden.

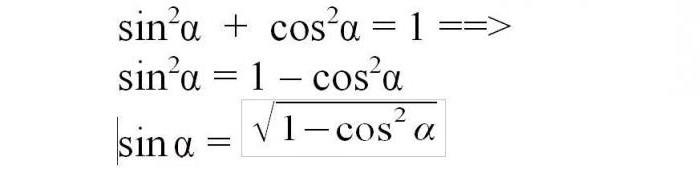
Jak znaleźć sinus przy znanej stycznej kąta? Styczną uzyskuje się dzieląc nogę przez środek lub dzieląc sinus przez cosinus. W ten sposób sinus jest produktem cosinusa i stycznej, a kwadrat sinusa jest kwadratem tego produktu. Zastąp cosinus w kwadracie różnicą między jednostką a kwadratem sinusoidalnym zgodnie z pierwszą tożsamością trygonometryczną i prostymi manipulacjami, dajemy równanie do obliczania kwadratowego sinusa przez styczną, odpowiednio, aby obliczyć, że sinus będzie musiał wyodrębnić pierwiastek wyniku.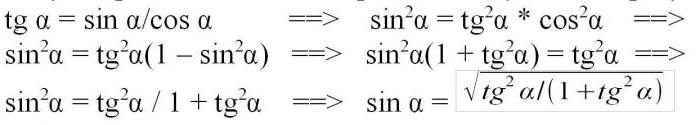

Jak znaleźć sinus przy znanym kącie cotangens? Wartość cotangensa może być obliczona przez podzielenie długości bliskiej nogi od kąta nogi przez duży dystans, a dzielenie cosinusa przez sinus, czyli cotangens jest funkcją odwrotną do stycznej liczby 1. Aby obliczyć sinus, można obliczyć styczną za pomocą wzoru tg α = 1 / ctg α i użyj wzoru w drugiej wersji. Możesz również wyprowadzić bezpośrednią formułę przez analogię ze styczną, która będzie wyglądać tak.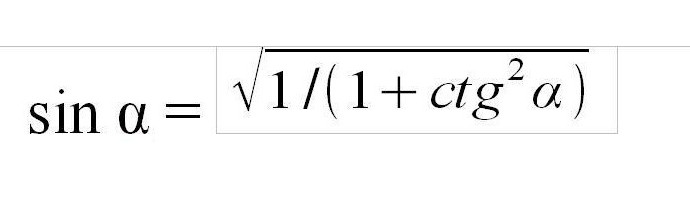

Jak znaleźć sinus po trzech stronach trójkąta

Istnieje formuła pozwalająca znaleźć długość nieznanej strony dowolnego trójkąta, nie tylko prostokąta, na dwóch znanych stronach przy użyciu trygonometrycznej funkcji cosinusu o przeciwnym kącie. Wygląda tak.

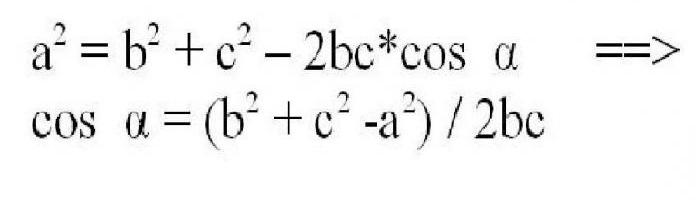Cóż, sinus może być dodatkowo obliczony przez cosinus zgodnie z powyższymi wzorami.