Jak utworzyć równanie prostej na dwóch punktach: dwuwymiarowych i trójwymiarowych
Linia prosta w geometrii jest jednym z najważniejszych elementów, ponieważ zbiera się z niej wiele postaci, zarówno na płaszczyźnie, jak iw przestrzeni. Wystarczy wymienić trójkąt, równoległobok, pryzmat, piramidę - wszystkie powstają przez przecięcie linii prostych. W tym artykule udzielono odpowiedzi na pytanie, w jaki sposób utworzyć równanie prostej z użyciem dwóch punktów.
Równanie linii dla przypadków dwuwymiarowych i trójwymiarowych
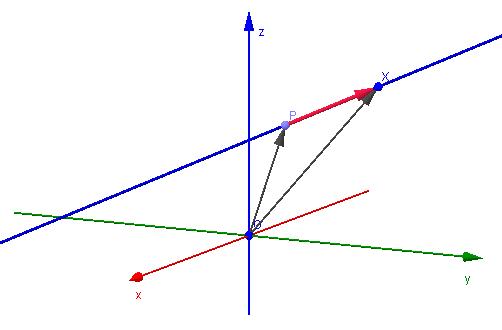
Przed przystąpieniem do dyskusji na temat tego, jak utworzyć równanie prostej z dwóch punktów, należy zrozumieć, o co toczy się gra.
Równanie linii prostej rozumiane jest jako równość związana z przyjętym układem współrzędnych, a wszystkie wartości zmiennych, które ją spełniają, muszą leżeć na jednej linii prostej. W przypadkach dwuwymiarowych i trójwymiarowych to równanie można zdefiniować w następujący sposób:
Ad
Q = P + α * u¯
Tutaj Q jest współrzędną dowolnego punktu linii, P jest współrzędną określonego punktu należącego do linii, u¯ jest kierunkiem wektora, α jest dowolną liczbą rzeczywistą. Wektor kierunkowy u jest równoległy do linii prostej. To wyrażenie jest nazywane równaniem parametryczno-wektorowym.
W przypadku dwuwymiarowym każdy punkt na płaszczyźnie jest jednoznacznie określony przez dwie współrzędne x i y, dzięki czemu można zapisać równanie linii w postaci:
(x; y) = (x 0 ; y 0 ) + α * (a; b)
Gdzie (x 0 ; y 0 ) są współrzędne znanego punktu linii, (a; b) są współrzędnymi wektora kierującego. W postaci parametrycznej to równanie można przepisać jako układ dwóch równań:
x = x 0 + a * a;
y = y 0 + α * b.
Wyrażając parametr alfa i porównując uzyskane równości, dochodzimy do formy:
y = b / a * x + (y 0 -x 0 * b / a) lub
y = A * x + C, gdzie A = b / a, C = (y 0 - x 0 * b / a)
Wynikowe wyrażenie jest znane każdemu uczniowi. Nazywa się to ogólnym równaniem linii na płaszczyźnie.
W przestrzeni, każdy punkt jest podany nie przez dwa, ale przez trzy współrzędne, dlatego jego równanie parametryczno-wektorowe przyjmuje postać:
(x; y; z) = (x 0 ; y 0 ; z 0 ) + α * (a; b; c)
Równanie parametryczno-wektorowe jest wygodne w użyciu, gdy trzeba wykonać równanie prostej przechodzącej przez dwa punkty.
Prosta linia i dwa punkty
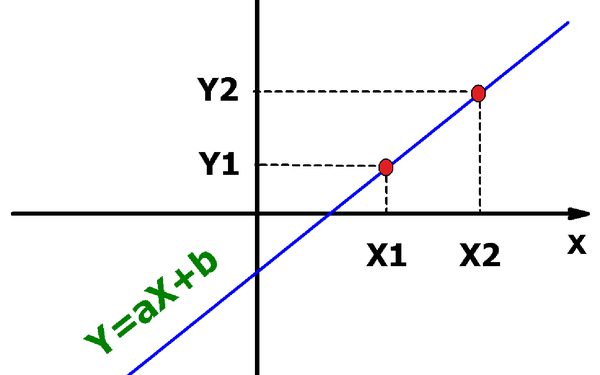
Teraz rozważ bezpośrednio kwestię artykułu. Jak zrobić bezpośrednie równanie za pomocą dwóch punktów? Najpierw otrzymujemy równanie na płaszczyźnie, a następnie uogólniamy je dla trójwymiarowego przypadku.
Załóżmy, że istnieją dwa punkty na płaszczyźnie P (x 1 ; y 1 ) i Q (x 2 ; y 2 ). Jeśli weźmiemy różnicę między współrzędnymi punktów, otrzymamy wektor, który jest kierowany od jednego z nich do drugiego. Ten wektor jest równy:
PQ¯ (x 2- x 1 ; y 2 -y 1 )
W tym przypadku PQ¯ jest kierowane od P (początek skierowanego segmentu) do Q (koniec). Ponieważ oba punkty należą do linii, należy do niej wektor PQ¯. Oznacza to, że można go uznać za przewodnik. Równanie linii prostej przyjmuje postać:
Ad
(x; y) = (x 1 ; y 1 ) + α * (x 2- x 1 ; y 2 -y 1 )
Tutaj przyjęliśmy punkt P. Jeśli zastąpimy go punktem Q, to równanie się nie zmieni.
Jak zrobić równanie prostej w przestrzeni za pomocą dwóch punktów? Podsumowując wynikową formułę dla samolotu, otrzymujemy:
(x; y; z) = (x 1 ; y 1 ; z 1 ) + β * (x 2- x 1 ; y 2 -y 1 ; z 2- z 1 )
Druga litera tego parametru została podjęta, aby pokazać niezależność tego i poprzednich równań.
Przykład rozwiązania problemu
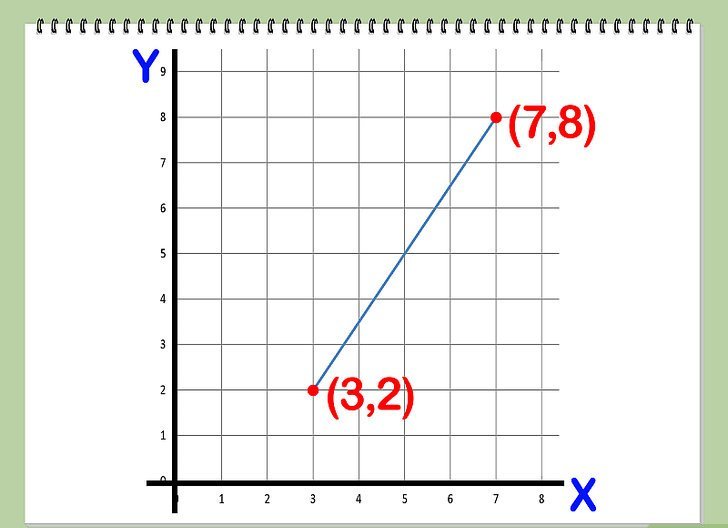
Po ustaleniu, jak utworzyć bezpośrednie równanie dla dwóch punktów, podajemy przykład wykorzystania wiedzy uzyskanej w przypadku dwuwymiarowym.
Załóżmy, że istnieją punkty na płaszczyźnie (3; -4) i (0; 7). Konieczne jest bezpośrednie równanie przez dwa punkty.
Oblicz współrzędne wektora prowadzącego:
(0-3; 7 - (- 4)) = (-3; 11)
Równanie parametryczno-wektorowe ma postać:
(x; y) = (3; -4) + α * (- 3; 11)
Otwórz go i przynieś do ogólnej postaci:
x = 3 - 3 * a => a = (x-3) / (- 3);
y = -4 + 11 * a => a = (y + 4) / 11;
(x-3) / (- 3) = (y + 4) / 11 =>
y = -11 / 3 * x + 7.
Otrzymaliśmy równanie w zwykłej (ogólnej) formie. Możesz zweryfikować jego ważność, zastępując współrzędne obu punktów ze stanu problemu.