Wprowadzenie do programowania dynamicznego

Wśród problemów rozwiązanych za pomocą programowania matematycznego możemy wyróżnić odrębną klasę problemów wymagających optymalizacji procesów wielostopniowych (wieloetapowych). Takie zadania są rozróżniane poprzez możliwość podzielenia rozwiązania na kilka powiązanych ze sobą kroków. Aby rozwiązać takie problemy, stosuje się programowanie dynamiczne lub, jak to się nazywa, programowanie wielostopniowe. Jego metody są zoptymalizowane pod kątem znalezienia optymalnego rozwiązania problemów wieloetapowych, które można podzielić na kilka etapów, etapów itp.

Pochodzenie terminu

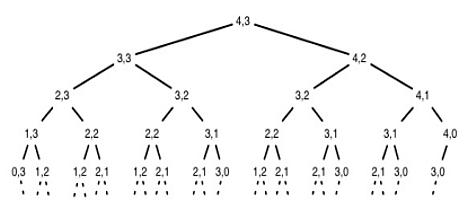
Użycie słowa "dynamic" w tytule początkowo zakładało, że podział na podzadania wystąpi głównie w czasie. Stosując metody dynamiczne do rozwiązywania zadań produkcyjnych, biznesowych i innych, które obejmują czynnik czasu, rozdzielenie na oddzielne etapy nie jest trudne. Ale możliwe jest zastosowanie techniki programowania dynamicznego w zadaniach, w których poszczególne etapy nie są powiązane w czasie. Zawsze w zadaniu wieloetapowym można wybrać parametr lub właściwość, zgodnie z którymi można podzielić na osobne kroki.

Algorytm (metoda) rozwiązywania problemów wieloetapowych

Algorytm lub Metoda programowania dynamicznego oparta jest na zasadzie sekwencyjnej optymalizacji problemu, gdy rozwiązanie ogólnego problemu dzieli się na szereg rozwiązań poszczególnych podzadań, a następnie integruje się je w jedno rozwiązanie. Bardzo często poszczególne podzadania są takie same, a jedno popularne rozwiązanie znacznie skraca czas obliczeń. 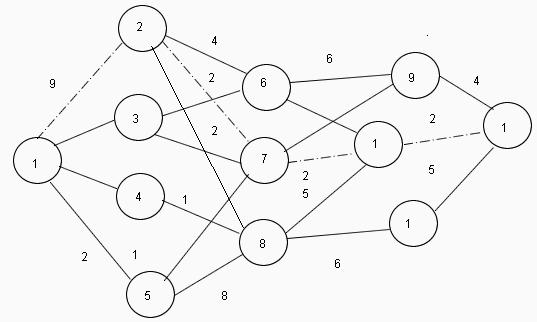Cechą tej metody jest autonomia rozwiązania problemu na każdym oddzielnym etapie, tj. Niezależnie od tego, jak proces został zoptymalizowany i rozwiązany na poprzednim etapie, obecne obliczenia wykorzystują tylko parametry procesu, które go charakteryzują w danym momencie. Na przykład, kierowca jadący drogą decyduje o aktualnej turze, bez względu na to, ile i jak długo jeździł.

Metoda powyżej i metoda poniżej

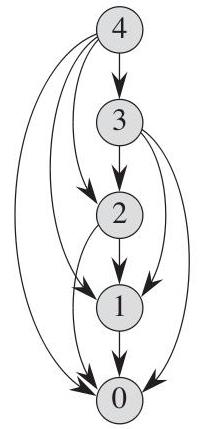
Pomimo faktu, że przy obliczaniu na oddzielnym etapie rozwiązywania problemu stosowane są parametry procesu dla bieżącej chwili, wynik optymalizacji na poprzednim etapie wpływa na obliczenia kolejnych etapów w celu uzyskania najlepszego wyniku w ogóle. Dynamiczne programowanie nazywa taką zasadę decyzji metodą optymalności, która określa, że ​​optymalna strategia rozwiązania problemu, niezależnie od początkowych decyzji i warunków, musi stanowić optymalną strategię dla stanu początkowego na kolejnych etapach. Jak widzimy, proces rozwiązywania problemu polega na ciągłej optymalizacji wyniku na każdym oddzielnym etapie od pierwszego do ostatniego. Ta metoda jest nazywana najlepszą metodą programowania. Rysunek pokazuje schematycznie algorytm rozwiązania od góry do dołu. Istnieje jednak szereg problemów wieloetapowych, w których maksymalny efekt jest już znany na ostatnim etapie, na przykład, już przybyliśmy z punktu A do punktu B, a teraz chcemy wiedzieć, czy prawidłowo poszliśmy na każdym z poprzednich etapów, czy też moglibyśmy zrobić coś bardziej optymalnie. Powstaje rekursywna sekwencja etapów, tj. Idziemy jakby "z przeciwnego". Ta metoda rozwiązania nosi nazwę "dolnej metody programowania".

Praktyczne zastosowanie

W dowolnym miejscu można zastosować programowanie dynamiczne pole działalności gdzie są procesy, które mogą dotyczyć dowolnego parametru (czas, ilość, temperatura itp.) podzielonego na kilka identycznych małych etapów. Najpowszechniej stosowane dynamiczne metody rozwiązania uzyskano w teorii sterowania i opracowywaniu systemów komputerowych.

Wyszukaj najlepszą ścieżkę

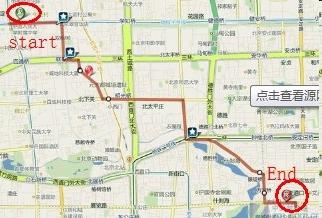
Dzięki dynamicznej optymalizacji możliwe jest rozwiązanie szerokiej klasy problemów związanych ze znalezieniem lub optymalizacją najkrótszej ścieżki i innymi problemami, w których "klasyczna" metoda wyliczania możliwych rozwiązań prowadzi do zwiększenia czasu obliczeń, a czasami jest ogólnie nie do przyjęcia. Klasycznym problemem programowania dynamicznego jest problem z plecakiem: podana jest pewna liczba obiektów o pewnej masie i koszcie, i konieczne jest wybranie zestawu obiektów o maksymalnej wartości i masie, która nie przekracza objętości plecaka. Klasyczne wyliczenie wszystkich opcji w poszukiwaniu optymalnego rozwiązania zajmie dużo czasu, a za pomocą metod dynamicznych problem zostanie rozwiązany w rozsądnym czasie. Zadania znalezienia najkrótszej ścieżki dla logistyki transportu są podstawowe, a dynamiczne metody rozwiązania są optymalnie dostosowane do ich rozwiązania. Najprostszym przykładem takiego zadania jest budowa najkrótszej trasy za pomocą samochodowego nawigatora GPS.

Produkcja

Dynamiczne programowanie jest szeroko stosowane w rozwiązywaniu różnych zadań produkcyjnych, takich jak zarządzanie zapasami, aby utrzymać wymaganą liczbę komponentów w dowolnym czasie, planowanie procesu produkcyjnego, konserwację i przegląd sprzętu, równomierne obciążenie personelu, najbardziej efektywną alokację funduszy inwestycyjnych itp. Aby rozwiązać problemy produkcyjne za pomocą dynamicznych metod programowania, opracowano specjalne pakiety oprogramowania, oraz Zintegrowany z popularnymi systemami zarządzania przedsiębiorstwem, takimi jak SAP.

Dziedzina naukowa

Metody programowania dynamicznego są szeroko stosowane w różnych badaniach naukowych. Na przykład są one z powodzeniem stosowane w algorytmach rozpoznawania mowy i obrazu, w przetwarzaniu dużych tablic danych w socjologii i działalność gospodarcza.