Analiza matematyczna i jej rola we współczesnym świecie

Historia

Filozofia jest uważana za punkt ciężkości wszystkich nauk, ponieważ zawierała pierwsze zarodki literatury, astronomii, literatury, nauk przyrodniczych, matematyki i innych dziedzin. Z biegiem czasu każdy obszar rozwijał się niezależnie, matematyka nie była wyjątkiem. Pierwszą "podpowiedź" analizy uważana jest za teorię rozkładu w nieskończenie małe wartości, do których próbowało podchodzić wiele umysłów, ale miała ona mglisty charakter i nie miała podstaw. Wynika to z przywiązania do starej szkoły nauk ścisłych w ścisłym brzmieniu. Isaac Newton był bardzo bliski powstania podstawy, ale się spóźnił. W rezultacie jego pojawienie się jako oddzielnego systemu analizy matematycznej jest obowiązkowe dla filozofa Gottfrieda Leibniza. To on w pracach przedstawił światu naukowemu takie pojęcia, w minimalnym i maksymalnym punkcie, przegięcia i wypukłości wykresu funkcji, sformułowały podstawy rachunku różniczkowego. Od tego momentu matematyka jest oficjalnie podzielona na elementarną i wyższą.

Analiza matematyczna. Nasze dni

Każda specjalność, czy to techniczna, czy humanitarna, obejmuje analizę w toku studiów. Głębokość badań jest różna, ale esencja pozostaje taka sama. Mimo całej "abstrakcyjności", jest to jeden z filarów, na których opiera się nauka przyrodnicza w jej współczesnym rozumieniu. Z jego pomocą opracowano fizykę i ekonomię, jest on w stanie opisać i przewidzieć działania giełdy, aby pomóc w stworzeniu optymalnego portfela akcji. Wprowadzenie do analizy matematycznej opiera się na elementarnych koncepcjach:

• zestawy;
• podstawowe operacje na zestawach;
• właściwości operacji na zestawach;
• funkcje (w przeciwnym razie odwzorowania);
• rodzaje funkcji;
• sekwencje;
• linie numeryczne;
• ograniczenie sekwencji;
• własności limitów;
• ciągłość funkcji.

Warto wyodrębnić takie pojęcia, jak: set, point, line, plane. Wszystkie nie mają definicji, ponieważ są to podstawowe pojęcia, na których zbudowana jest cała matematyka. Wszystko, co można zrobić w procesie pracy, to wyjaśnić, co dokładnie oznaczają w poszczególnych przypadkach.

Limit jako kontynuacja

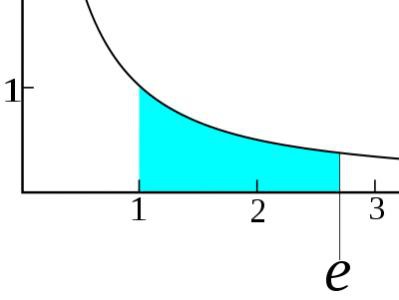Podstawą analizy matematycznej jest limit. W praktyce jest to wartość, do której dąży sekwencja lub funkcja, przychodzi tak blisko, jak chce, ale jej nie osiąga. Jest on oznaczony przez lim; rozpatrujemy specjalny przypadek limitu funkcji: lim (x-1) = 0 jako x → 1. Z tego najprostszego przykładu jest jasne, że jako x → 1, cała funkcja dąży do 0, ponieważ jeśli podstawimy ten limit do samej funkcji, otrzymamy (1-1) = 0. Bardziej szczegółowo, od elementarnych do skomplikowanych przypadków szczególnych, informacja jest przedstawiona w formie analizy "Biblii" - dzieła Fichtenholza. Tam rozważane jest to w kontekście analizy matematycznej, limitów, ich wyprowadzania i dalszego stosowania. Na przykład wyprowadzenie liczby e (stała Eulera) byłoby niemożliwe bez teorii ograniczeń. Pomimo dynamicznej abstrakcyjności teorii granice są aktywnie wykorzystywane w praktyce w tej samej ekonomii i socjologii. Na przykład nie można obejść się bez nich, naliczając odsetki od lokaty bankowej.