Hipotezy Poincare: historia problemu, dowód, znaczenie

W szkole wszyscy znają pojęcia twierdzenia i hipotezy. Co do zasady, najprostsze i najbardziej prymitywne prawa mają wpływ na życie, podczas gdy matematycy tworzą bardzo złożone założenia i stwarzają interesujące problemy. Nie zawsze, oni sami potrafią znaleźć rozwiązania i dowody, aw niektórych przypadkach ich zwolennicy i koledzy po prostu walczą od wielu lat.

Instytut Clay w 2000 r. Opracował listę 7 tak zwanych Wyzwań Milenijnych, analogicznie do listy hipotez zebranych w 1900 r. Prawie wszystkie te zadania zostały już rozwiązane, tylko jeden z nich został przeniesiony do zaktualizowanej wersji. Teraz lista problemów wygląda następująco:

• Domysły Hodge'a;
• równość klas P i NP;
• Hipoteza Poincarego;
• Teoria Yanga-Millsa;
• Hipoteza Riemanna;
• istnienie i płynność rozwiązywania równań Naviera-Stokesa;
• Hipoteza Birch-Swinnerton-Dyer.

Wszystkie należą do różnych dyscyplin w obrębie matematyki i są ważne. Na przykład równania Naviera-Stokesa odnoszą się do hydrodynamiki, ale w praktyce mogą opisywać zachowanie substancji w magmie ziemskiej lub być przydatne w przewidywaniu pogody. Ale wszystkie te problemy wciąż szukają dowodu lub odmowy. Z wyjątkiem jednego.

Twierdzenie Poincarego

Trudno jest wyjaśnić w prosty sposób, czym jest problem, ale można spróbować. Wyobraź sobie kulę, na przykład bańkę. Wszystkie punkty jego powierzchni są w równej odległości od jej środka, który do niej nie należy. Ale jest to ciało dwuwymiarowe, a hipoteza mówi o trójwymiarowości. Nie można już tego sobie wyobrazić, ale mamy matematykę teoretyczną. W tym przypadku oczywiście wszystkie punkty tego ciała zostaną również usunięte z centrum.

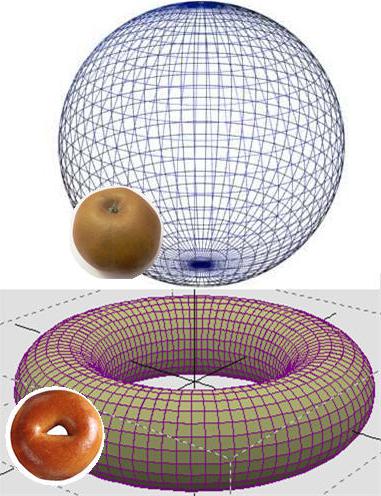
Ten problem dotyczy topologii - nauki o właściwościach kształtów geometrycznych. Jednym z podstawowych terminów jest homeomorfizm, to jest wysoki stopień podobieństwa. Aby dać przykład, możesz wyobrazić sobie piłkę i torus. Jedna postać nie może być uzyskana od innej, unikając pęknięć, ale stożek, sześcian lub cylinder od pierwszego można uzyskać całkiem łatwo. Oto hipoteza Poincarego i poświęcona tym metamorfozom z jedną tylko różnicą - mówimy o wielowymiarowej przestrzeni i ciałach.

Historia

Francuski matematyk Henri Poincare studiował różne dziedziny nauki. O swoich osiągnięciach można powiedzieć, na przykład, że niezależnie od Alberta Einsteina przedstawił główne przepisy specjalna teoria względności. W 1904 r. Podniósł problem udowodnienia, że ​​jakiekolwiek trójwymiarowe ciało, które posiada pewne właściwości sfery, jest dokładnie do deformacji. Później został rozszerzony i uogólniony, i stał się szczególnym przypadkiem hipotezy Thurstona sformułowanej w 1982 roku.

Sformułowanie

Poincaré początkowo pozostawił takie stwierdzenie: każdy po prostu połączony zwarty trójwymiarowy kolektor bez granicy jest homeomorficzny do sfery trójwymiarowej. Później został rozszerzony i uogólniony. A jednak przez długi czas było to pierwotne zadanie, które spowodowało najwięcej problemów i zostało rozwiązane zaledwie 100 lat po jego pojawieniu się.

Interpretacja i znaczenie

To jest homeomorfizm, to już zostało omówione. Teraz warto mówić o zwartości i osobliwości. Pierwszy oznacza tylko, że odmiana ma ograniczone rozmiary, nie może być ciągła i nieskończenie rozciągnięta.

Jeśli chodzi o wyjątkowość, możesz spróbować podać prosty przykład. Dwuwymiarowa kula - jabłko - ma jedną interesującą właściwość. Jeśli weźmiesz zwykłą gumę zamkniętą i przymocujesz ją do powierzchni, wówczas gładkie odkształcenie może zostać zredukowane do jednego punktu. Jest to właściwość wyjątkowości, ale przedstawienie jej w stosunku do trójwymiarowa przestrzeń dość trudne.

Mówiąc po prostu, problemem było udowodnienie, że osobliwość jest unikalną własnością sfery. A jeśli relatywnie rzecz biorąc, doświadczenie z gumką zakończyło się takim wynikiem, to ciało jest homeomorficzne. Jeśli chodzi o zastosowanie tej teorii do życia, Poincare wierzył, że Wszechświat, w pewnym sensie, jest przestrzenią trójwymiarową.

Dowód

Nie myśl, że spośród dziesiątków matematyków, którzy pracowali na całym świecie, nikt nie opracował ani jednej joty, rozwiązując ten problem. Wręcz przeciwnie, nastąpił postęp, który ostatecznie doprowadził do wyniku. Sam Poincaré nie miał czasu na dokończenie pracy, ale jego badania poważnie podniosły całą topologię.

W latach trzydziestych powróciło zainteresowanie hipotezą. Przede wszystkim sformułowanie zostało rozszerzone na "przestrzeń n-wymiarową", a następnie amerykański Whitehead zrelacjonował udane dowody, później je porzucając. W latach 60-70 dwóch matematyków naraz - Smale i Stallings - prawie jednocześnie, ale na różne sposoby opracowali rozwiązanie dla wszystkich n większych niż 4.

W 1982 roku, a dla 4 znaleziono dowody, pozostało tylko 3. W tym samym roku Thurston sformułował hipotezę geometryzacji, a teoria Poincaré stała się jej szczególnym przypadkiem.

Potem praca została nieco utknęły w martwym punkcie - amerykański Richard Hamilton zaproponował wykorzystanie przepływu Ricci w rozwiązaniu, ale napotkał trudności i nie ukończył badań.

Przez 20 lat hipoteza Poincaré była jakby zapomniana. W 2002 r. Rosyjski matematyk Grigori Perelman przedstawił ogólne rozwiązanie, a sześć miesięcy później wprowadził pewne poprawki. Później te dowody zostały przetestowane i doprowadzone do "zabłyśnięcia" przez amerykańskich i chińskich naukowców. I sam Perelman stracił zainteresowanie problemem, chociaż rozwiązał bardziej ogólny problem geometryzacji, o którym przypuszczenie Poincarégo jest tylko przypadkiem specjalnym.

Uznanie i ocena

Oczywiście natychmiast stało się to sensacją, ponieważ rozwiązanie jednego z problemów milenijnych po prostu nie mogło zostać przeoczone. Jeszcze bardziej zaskakujący był fakt, że Gregory Perelman odmówił wszystkich nagród i nagród, mówiąc, że już miał cudowne życie. W umysłach zwykłych ludzi natychmiast stał się przykładem tego na wpół szalonego geniusza, który interesuje się wyłącznie nauką.

Wszystko to spowodowało wiele dyskusji w prasie i mediach, że popularność matematyka stała się jego. Latem 2014 roku pojawiły się informacje, że Perelman wyjechał do pracy w Szwecji, ale okazało się, że to tylko plotka, nadal mieszka skromnie w Petersburgu i prawie nie komunikuje się z nikim. Wśród przyznanych mu nagród była nie tylko Nagroda Instytutu Clay, ale także prestiżowy Medal Fieldsa, ale odmówił wszystkiego. Jednak Hamilton, który, według szacunków Perelmana, nie mniej ważny wkład do dowodu, również nie został zapomniany. W 2009 i 2011 roku zdobył także kilka prestiżowych nagród i wyróżnień.

Refleksja kulturowa

Mimo że dla zwykłych obywateli zarówno oświadczenie, jak i rozwiązanie tego problemu nie mają większego sensu, dowody stały się znane dość szybko. W 2008 r. Japoński reżyser Masahito Kasuga sfilmował z tej okazji film dokumentalny "The Enchantment of the Poincaré Hypothesis", poświęcony 100-letnim próbom rozwiązania tego problemu.

Wielu matematyków zaangażowanych w ten problem brało udział w strzelaniu, ale główny bohater, Grigorij Perelman, nie chciał tego robić. Mniej więcej jego bliscy przyjaciele byli również zaangażowani w strzelaninę. Film dokumentalny, pojawiający się na ekranach po publicznym oddźwięku w związku z odmową przyjęcia nagrody przez naukowca, zdobył sławę w niektórych kręgach, a także otrzymał kilka nagród. Jeśli chodzi o kultura masowa, zwykli ludzie wciąż zastanawiają się, do jakich argumentów prowadził się petersburski matematyk, odmawiając wzięcia pieniędzy, kiedy mógł je oddać, na przykład na cele charytatywne.