Prawdopodobieństwo zdarzenia Określanie prawdopodobieństwa zdarzenia

Początkowo, będąc jedynie zbiorem informacji i empirycznych obserwacji gry w kości, teoria prawdopodobieństwa stała się solidną nauką. Pierwszym, który dał jej ramy matematyczne były Farm i Pascal.

Od myślenia o teorii wiecznej do prawdopodobieństwa

Dwie osoby, dla których teoria prawdopodobieństwa zawdzięcza wiele podstawowych formuł, Blaise Pascal i Thomas Bayes, są znane jako głęboko religijni ludzie, z których ostatni jest prezbiteriańskim kapłanem. Wygląda na to, że pragnienie tych dwóch naukowców, aby udowodnić fałszywość opinii na temat pewnej fortuny, dając szczęście zwierzętom domowym, dało impuls do badań w tej dziedzinie. Wszakże każda gra losowa z jej wygranymi i stratami jest po prostu symfonią zasad matematycznych.

Dzięki ekscytacji kawalera de Meré, który był równie graczem i osobą nieobojętną dla nauki, Pascal musiał znaleźć sposób na obliczenie prawdopodobieństwa. De Mere był zainteresowany takim pytaniem: "Ile razy trzeba rzucać dwiema parami, aby uzyskać 12 punktów więcej niż 50%?" Drugie pytanie, bardzo zainteresowane dżentelmenem: "Jak podzielić zakład pomiędzy uczestnikami niedokończonej gry?" Oczywiście Pascal skutecznie odpowiedział na oba pytania de Mere, który stał się nieświadomym inicjatorem rozwoju teorii prawdopodobieństwa. Co ciekawe, persona de Mere była znana w tej dziedzinie, a nie w literaturze.

Wcześniej żaden matematyk nie podejmował prób obliczenia prawdopodobieństw zdarzeń, ponieważ uważano, że była to tylko decyzja wróżbiarska. Blaise Pascal podał pierwszą definicję prawdopodobieństwa zdarzenia i pokazał, że jest to konkretna liczba, którą można udowodnić matematycznie. Teoria prawdopodobieństwa stała się podstawą statystyki i jest szeroko stosowana we współczesnej nauce.

Co to jest wypadek

Jeśli weźmiemy pod uwagę test, który można powtórzyć nieskończoną liczbę razy, możemy zdefiniować zdarzenie losowe. Jest to jeden z prawdopodobnych wyników eksperymentu.

Doświadczenie to realizacja konkretnych działań w niezmienionych warunkach.

Aby pracować z rezultatami doświadczenia, zdarzenia są zwykle oznaczone literami A, B, C, D, E ...

Prawdopodobieństwo zdarzenia losowego

Aby przejść do matematycznej części prawdopodobieństwa, konieczne jest zdefiniowanie wszystkich jego składników.

Prawdopodobieństwo zdarzenia jest wyrażoną liczbowo miarą możliwości wystąpienia określonego zdarzenia (A lub B) w wyniku doznania. Oznacza prawdopodobieństwo jako P (A) lub P (B).

W teorii prawdopodobieństwa wyróżniono:

• w wyniku eksperymentu P (Ω) = 1 wystąpi niezawodne zdarzenie;
• niemożliwe wydarzenie nigdy nie może wystąpić P (Ø) = 0;
• zdarzenie losowe leży pomiędzy wiarygodnym i niemożliwym, to znaczy prawdopodobieństwo jego wystąpienia jest możliwe, ale nie gwarantowane (prawdopodobieństwo wystąpienia zdarzenia losowego jest zawsze w zakresie 0≤P (A) ≤ 1).

Relacja między zdarzeniami

Weź pod uwagę zarówno jedną, jak i sumę zdarzeń A + B, gdy zdarzenie ma wpływ na implementację co najmniej jednego ze składników, A lub B, lub obu - A i B.

W stosunku do siebie zdarzenia mogą być:

• Równy z.
• Kompatybilny.
• Niezgodny.
• Przeciwny (wzajemnie wykluczający).
• Zależny.

Jeśli dwa zdarzenia mogą wystąpić z równym prawdopodobieństwem, wówczas są one równie możliwe .

Jeżeli wystąpienie zdarzenia A nie niweczy prawdopodobieństwa wystąpienia zdarzenia B, wówczas są one zgodne.

Jeśli zdarzenia A i B nigdy nie występują jednocześnie w tym samym doświadczeniu, są one nazywane niekompatybilnymi . Rzucanie monetą jest dobrym przykładem: pojawienie się ogonów jest automatycznie nieobecnością orła.

Prawdopodobieństwo sumy takich niezgodnych zdarzeń składa się z sumy prawdopodobieństw każdego z wydarzeń:

((А + В) = ((А) + ((В)

Jeśli wystąpienie jednego zdarzenia uniemożliwia wystąpienie drugiego, wówczas nazywa się je przeciwieństwem. Wtedy jeden z nich jest oznaczony jako A, a drugi - (odczytany jako "nie A"). Wystąpienie zdarzenia A oznacza, że ​​Ā nie wystąpiło. Te dwa zdarzenia tworzą kompletną grupę z sumą prawdopodobieństw równą 1.

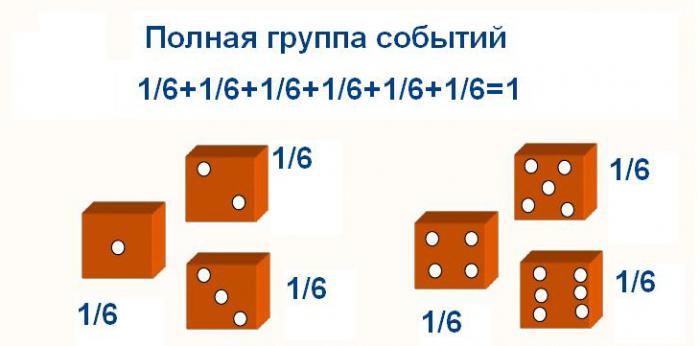
Zdarzenia zależne mają wzajemny wpływ, zmniejszając lub zwiększając prawdopodobieństwo siebie nawzajem.

Relacja między zdarzeniami. Przykłady

Na przykładach znacznie łatwiej jest zrozumieć zasady teorii prawdopodobieństwa i kombinację zdarzeń.

Doświadczenie, które zostanie przeprowadzone, polega na wyciągnięciu kulek z pudełka, a wynik każdego doświadczenia jest elementarnym wynikiem.

Wydarzenie jest jednym z możliwych wyników tego doświadczenia - czerwoną kulką, niebieską kulką, piłką z numerem sześć i tak dalej.

Test numer 1. W grze bierze udział 6 piłek, z których trzy mają kolor niebieski, numery nieparzyste stosuje się do nich, a pozostałe trzy są czerwone z liczbami parzystymi.

Test numer 2. Jest 6 niebieskich kulek z liczbami od 1 do 6.

Na podstawie tego przykładu możesz wykonywać połączenia:

• Wiarygodne wydarzenie. W języku hiszpańskim Zdarzenie 2 "dostać niebieską piłkę" jest wiarygodne, ponieważ prawdopodobieństwo jego wystąpienia wynosi 1, ponieważ wszystkie piłki są niebieskie i nie może być braków. Podczas imprezy "zdobywaj piłkę z numerem 1" - losowo.
• Niemożliwe wydarzenie. W języku hiszpańskim №1 z niebieskich i czerwonych kulek wydarzenie "dostać fioletową kulkę" jest niemożliwe, ponieważ prawdopodobieństwo jego wystąpienia wynosi 0.
• Równe wydarzenia. W języku hiszpańskim Wydarzenia z numerem 1 "zdobywaj piłkę z numerem 2" i "otrzymuj piłkę z numerem 3" są jednakowo możliwe, a wydarzenia "zdobywaj piłkę z liczbą parzystą" i "otrzymaj piłkę z numerem 2" mają inne prawdopodobieństwo.
• Zgodne zdarzenia. Dwa razy z rzędu, aby uzyskać szóstkę w trakcie rzutu kostką - są to zgodne zdarzenia.
• Niezgodne zdarzenia. W tym samym pliku isp. Zdarzenia №1 "dostać czerwoną piłkę" i "dostać piłkę z nieparzystą liczbą" nie mogą być łączone w tym samym doświadczeniu.
• Wydarzenia przeciwne. Najbardziej jaskrawym tego przykładem są rzucanie monetami, kiedy pociągnięcie orła jest równoznaczne z nie wyciąganiem ogonów, a suma ich prawdopodobieństw wynosi zawsze 1 (pełna grupa).
• Zdarzenia zależne . Tak, po hiszpańsku. Nr 1 można ustawić, aby wyodrębnić czerwoną piłkę dwa razy z rzędu. Jego ekstrakcja lub brak ekstrakcji po raz pierwszy wpływa na prawdopodobieństwo ekstrakcji po raz drugi.

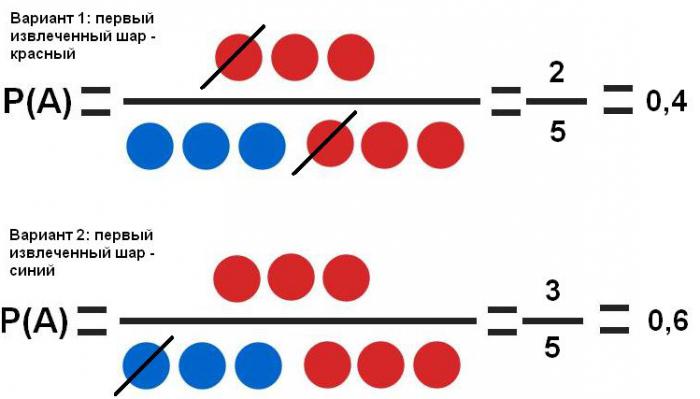
Widać, że pierwsze zdarzenie znacząco wpływa na prawdopodobieństwo drugiego (40% i 60%).

Formuła prawdopodobieństwa zdarzeń

Przejście od wróżbiarskich odbić do dokładnych danych następuje poprzez przeniesienie tematu na płaszczyznę matematyczną. Oznacza to, że osądy dotyczące zdarzenia losowego, takie jak "wysokie prawdopodobieństwo" lub "minimalne prawdopodobieństwo", można przetłumaczyć na konkretne dane liczbowe. Taki materiał jest już dopuszczalny do oceny, porównywania i wprowadzania do bardziej złożonych obliczeń.

Z punktu widzenia kalkulacji określenie prawdopodobieństwa zdarzenia jest stosunkiem liczby elementarnych pozytywnych wyników do liczby wszystkich możliwych wyników doświadczenia w stosunku do określonego zdarzenia. Prawdopodobieństwo jest oznaczone przez P (A), gdzie P oznacza słowo "probabilit", które z francuskiego jest tłumaczone jako "prawdopodobieństwo".

Tak więc formuła prawdopodobieństwa zdarzeń:

P (A) = m / n,

Gdzie m jest liczbą korzystnych wyników dla zdarzenia A, n jest sumą wszystkich możliwych wyników dla tego doświadczenia. W takim przypadku prawdopodobieństwo zdarzenia zawsze wynosi od 0 do 1:

0 ≤ P (A) ≤ 1.

Obliczanie prawdopodobieństwa zdarzenia. Przykład

Weź sp. Nr 1 z kulkami, jak opisano wcześniej: 3 niebieskie kule z numerami 1/3/5 i 3 czerwone z numerami 2/4/6.

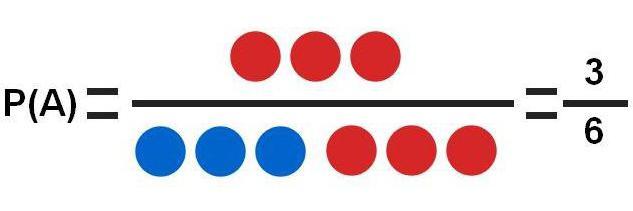
Na podstawie tego testu można rozważyć kilka różnych zadań:

• A - utrata czerwonej piłki. Są 3 czerwone kule, a łącznie jest ich 6, jest to najprostszy przykład, w którym prawdopodobieństwo zdarzenia wynosi P (A) = 3/6 = 0,5.
• B - utrata liczby parzystej. Suma liczb parzystych wynosi 3 (2,4,6), a całkowita liczba możliwych wariantów numerycznych wynosi 6. Prawdopodobieństwo tego zdarzenia wynosi P (B) = 3/6 = 0,5.
• C - utrata liczby większej niż 2. Łącznie istnieją 4 takie opcje (3,4,5,6) z całkowitej liczby możliwych wyników 6. Prawdopodobieństwo zdarzenia C jest równe P (C) = 4/6 = 0,67.

Jak wynika z obliczeń, zdarzenie C ma większe prawdopodobieństwo, ponieważ liczba prawdopodobnych pozytywnych wyników jest wyższa niż w A i B.

Niezgodne zdarzenia

Takie zdarzenia nie mogą jednocześnie pojawić się w tym samym doświadczeniu. Jak w języku hiszpańskim Nr 1 nie można jednocześnie uzyskać niebieskiej i czerwonej kulki. Oznacza to, że można uzyskać niebieską lub czerwoną piłkę. Podobnie w kościach nie mogą pojawić się równomiernie w tym samym czasie. nieparzysta liczba.

Prawdopodobieństwo wystąpienia dwóch zdarzeń jest uważane za prawdopodobieństwo ich sumy lub produktu. Suma takich zdarzeń A + B jest uważana za takie zdarzenie, które polega na pojawieniu się zdarzenia A lub B, oraz na produkcie ich AB - w wyglądzie obu. Na przykład pojawienie się dwóch szóstek naraz na twarzach dwóch kości w jednym rzucie.

Suma kilku zdarzeń jest wydarzeniem, które obejmuje pojawienie się co najmniej jednego z nich. Stworzenie kilku wydarzeń jest wspólnym pojawieniem się ich wszystkich.

W teorii prawdopodobieństwa, z reguły użycie związku "i" oznacza sumę, związek "lub" - mnożenie. Formuły z przykładami pomogą zrozumieć logikę dodawania i mnożenia w teorii prawdopodobieństwa.

Prawdopodobieństwo sumy niespójnych zdarzeń

Jeżeli rozważane jest prawdopodobieństwo niezgodności zdarzeń, prawdopodobieństwo wystąpienia sumy zdarzeń jest równe dodaniu ich prawdopodobieństw:

((А + В) = ((А) + ((В)

Na przykład: obliczyć prawdopodobieństwo, że w sp. №1 z niebieskimi czerwonymi kulkami wypadnie liczbą od 1 do 4. Obliczamy nie w jednym działaniu, ale sumę prawdopodobieństw elementów elementarnych. Tak więc, w tym doświadczeniu, tylko 6 kulek lub 6 możliwych wyników. Liczby, które spełniają warunek, wynoszą 2 i 3. Prawdopodobieństwo wystąpienia 2 wypadków wynosi 1/6, a prawdopodobieństwo 3 wynosi również 1/6. Prawdopodobieństwo, że liczba od 1 do 4 wypadnie, jest równe:

1/6 + 1/6 = 1/3

Prawdopodobieństwo sumy niezgodnych zdarzeń z całej grupy wynosi 1.

Jeśli więc w eksperymencie z kostką sumujemy prawdopodobieństwa zrzucenia wszystkich cyfr, to w rezultacie otrzymujemy jeden.

Odnosi się to również do przeciwnych zdarzeń, na przykład w przypadku doświadczenia z monetą, gdzie jedna strona jest zdarzeniem A, a druga zdarzeniem przeciwnym - jak dobrze wiadomo

((А) + ((Ā) = 1

Prawdopodobieństwo wystąpienia niezgodnych zdarzeń

Mnożenie prawdopodobieństw jest używane przy rozważaniu wystąpienia dwóch lub więcej niezgodnych zdarzeń w pojedynczej obserwacji. Prawdopodobieństwo wystąpienia w nim zdarzeń A i B jest równe iloczynowi ich prawdopodobieństw, lub:

((А * В) = ((А) * ((В)

Na przykład prawdopodobieństwo, że w sp. # 1 w wyniku dwóch prób dwukrotnie pojawi się niebieska kula, równa się

½ * ½ = ¼

Oznacza to, że prawdopodobieństwo zdarzenia, gdy w wyniku dwóch prób ekstrakcji piłek tylko niebieskie kulki zostaną wyodrębnione, wynosi 25%. Przeprowadzenie praktycznych eksperymentów w tym zadaniu jest bardzo proste i zobacz, czy tak jest naprawdę.

Wspólne wydarzenia

Zdarzenia uznaje się za połączone, gdy pojawienie się jednego z nich może się pokrywać z wyglądem drugiego. Pomimo tego, że są połączone, bierze się pod uwagę prawdopodobieństwo niezależnych zdarzeń. Na przykład rzucanie dwiema kośćmi może dać wynik, gdy figurka 6 spadnie na obie z nich.Jednak wydarzenia zbiegły się i pojawiły się w tym samym czasie, są one niezależne od siebie - tylko jedna szóstka może spaść, druga kość nie ma na nią wpływu.

Prawdopodobieństwo wspólnych zdarzeń jest traktowane jako prawdopodobieństwo ich sumy.

Prawdopodobieństwo sumy wspólnych wydarzeń. Przykład

Prawdopodobieństwo sumy zdarzeń A i B, które są ze sobą powiązane, jest równe sumie prawdopodobieństw zdarzenia minus prawdopodobieństwo ich pracy (tj. Ich wspólne wdrożenie):

_Wspólne R. (A + B) = P (A) + P (B) - P (AB)

Załóżmy, że prawdopodobieństwo trafienia w cel pojedynczym strzałem wynosi 0,4. Następnie zdarzenie A - trafienie w cel w pierwszej próbie, B - w drugim. Te wydarzenia są wspólne, ponieważ możliwe jest, że możesz trafić cel z pierwszego i drugiego strzału. Ale wydarzenia nie są zależne. Jakie jest prawdopodobieństwo wystąpienia zdarzenia pokonania celu dwoma strzałami (przynajmniej jednym)? Zgodnie ze wzorem:

0,4 + 0,4-0,4 * 0,4 = 0,64

Odpowiedź na pytanie brzmi: "Prawdopodobieństwo trafienia celu z dwóch strzałów wynosi 64%."

Ta formuła prawdopodobieństwa zdarzenia może być również zastosowana do niezgodnych zdarzeń, gdzie prawdopodobieństwo wspólnego wystąpienia zdarzenia P (AB) wynosi 0. Oznacza to, że prawdopodobieństwo sumy niezgodnych zdarzeń można uznać za specjalny przypadek proponowanej formuły.

Geometria prawdopodobieństwa dla przejrzystości

Co ciekawe, prawdopodobieństwo sumy zdarzeń wspólnych można przedstawić w postaci dwóch regionów A i B, które przecinają się ze sobą. Jak widać na zdjęciu, obszar ich powiązania jest równy powierzchni całkowitej minus powierzchnia ich przecięcia. To geometryczne wyjaśnienie sprawia, że ​​formuła nielogiczna na pierwszy rzut oka jest bardziej zrozumiała. Zwróć uwagę, że rozwiązania geometryczne nie są rzadkością w teorii prawdopodobieństwa.

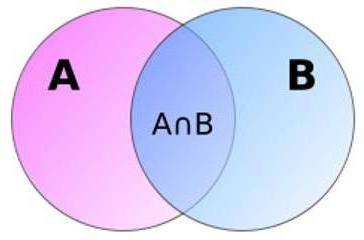
Ustalenie prawdopodobieństwa sumy zestawu (więcej niż dwóch) wspólnych wydarzeń jest raczej kłopotliwe. Aby to obliczyć, musisz użyć formuł przewidzianych dla tych przypadków.

Zdarzenia zależne

Zdarzenia zależne są wywoływane, jeśli wystąpienie jednego (A) z nich wpływa na prawdopodobieństwo wystąpienia innego (B). Ponadto brany jest pod uwagę wpływ zarówno wystąpienia zdarzenia A, jak i jego nieobecności. Chociaż zdarzenie jest określane jako zależne z definicji, tylko jedna z nich jest zależna (B). Zwykłe prawdopodobieństwo jest oznaczane jako P (B) lub prawdopodobieństwo niezależnych zdarzeń. W przypadku osób na utrzymaniu wprowadza się nową koncepcję - prawdopodobieństwo warunkowe P _A (B), które jest prawdopodobieństwem zdarzenia zależnego B pod warunkiem, że wystąpiło zdarzenie A (hipoteza), od którego to zależy.

Ale zdarzenie A jest również przypadkowe, dlatego ma również prawdopodobieństwo, że musi i może być brane pod uwagę w wykonywanych obliczeniach. Następnie, przykład pokaże, jak pracować z zależnymi zdarzeniami i hipotezą.

Przykład obliczenia prawdopodobieństwa wystąpienia zdarzeń zależnych

Dobrym przykładem do obliczania zdarzeń zależnych może być standardowa talia kart.

Na przykładzie talii złożonej z 36 kart, rozważamy zdarzenia zależne. Konieczne jest określenie prawdopodobieństwa, że ​​druga karta, wyjęta z talii, będzie należała do koloru diamentu, jeżeli pierwsza karta to:

1. Diamenty
2. Kolejny kolor.

Jest oczywiste, że prawdopodobieństwo drugiego zdarzenia B zależy od pierwszego A. Tak więc, jeśli pierwsza opcja jest ważna, że ​​w talii była 1 karta (35) i 1 diament (8) mniej, prawdopodobieństwo zdarzenia B:

P _A (B) = 8/35 = 0,23

Jeśli druga opcja jest ważna, w talii znajduje się 35 kart, a pełna liczba tamburynów (9) jest nadal zachowana, a następnie prawdopodobieństwo następnego zdarzenia B:

_A (В) = 9/35 = 0,26.

Można zauważyć, że jeśli zdarzenie A jest uwarunkowane faktem, że pierwsza karta jest tamburynem, wówczas prawdopodobieństwo zdarzenia B maleje, i na odwrót.

Mnożenie zależnych zdarzeń

Kierując się poprzednim rozdziałem, akceptujemy pierwsze zdarzenie (A) jako fakt, ale jeśli mówić w istocie, jest ono przypadkowe. Prawdopodobieństwo tego zdarzenia, a mianowicie wydobycie diamentów z talii kart, jest równe:

P (A) = 9/36 = 1/4

Ponieważ teoria sama w sobie nie istnieje, ale ma służyć praktycznym celom, należy zauważyć, że najczęściej konieczne jest prawdopodobieństwo wystąpienia zdarzeń zależnych.

Zgodnie z twierdzeniem o iloczynie prawdopodobieństw zdarzeń zależnych, prawdopodobieństwo wystąpienia wspólnie zależnych zdarzeń A i B jest równe prawdopodobieństwu jednego zdarzenia A przemnożone przez warunkowe prawdopodobieństwo zdarzenia B (zależne od A):

P (AB) = P (A) * P _A (B)

Następnie, w przykładzie z talią, prawdopodobieństwo wyodrębnienia dwóch kart w kolorze diamentu wynosi:

9/36 * 8/35 = 0,0571 lub 5,7%

A prawdopodobieństwo wydobycia na początku nie jest tamburynem, a następnie tamburynem, jest równa:

27/36 * 9/35 = 0,19 lub 19%

Można zauważyć, że prawdopodobieństwo wystąpienia zdarzenia B jest większe, pod warunkiem, że najpierw zostanie wyodrębniona karta koloru, inna niż diamenty. Ten wynik jest dość logiczny i zrozumiały.

Całkowite prawdopodobieństwo zdarzenia

Kiedy problem z prawdopodobieństwami warunkowymi staje się wieloaspektowy, nie można go obliczyć przy użyciu konwencjonalnych metod. Gdy istnieje więcej niż dwie hipotezy, a mianowicie A1, A2, ..., A _n , ... tworzy kompletną grupę zdarzeń, pod warunkiem że:

• P (A _i )> 0, i = 1,2, ...
• A _i ∩ A _j = Ø, i ≠ j.
• Σ _k A _k = Ω.

Tak więc formuła całkowitego prawdopodobieństwa zdarzenia B z pełną grupą zdarzeń losowych A1, A2, ..., A _n jest równa _:

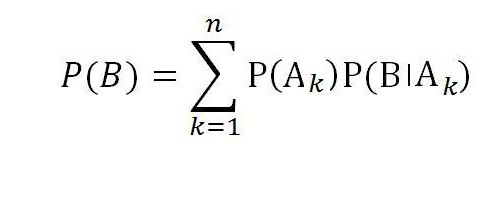
Patrząc w przyszłość

Prawdopodobieństwo zdarzenia losowego jest niezbędne w wielu dziedzinach nauki: ekonometrii, statystyce, fizyce itp. Ponieważ niektórych procesów nie można określić deterministycznie, ponieważ same z natury mają charakter probabilistyczny, potrzebne są specjalne metody pracy. Teoria prawdopodobieństwa zdarzenia może być wykorzystana w dowolnej dziedzinie technologicznej jako sposób określenia prawdopodobieństwa błędu lub nieprawidłowego działania.

Można powiedzieć, że rozpoznając prawdopodobieństwo, w pewien sposób podejmujemy teoretyczny krok w przyszłość, badając go przez pryzmat formuł.