Prawy trójkąt i jego właściwości
Trójkąt prostokątny to trójkąt, którego jeden kąt jest prosty (równy 90 0 ). Dlatego pozostałe dwa kąty sumują się do 90 0 .
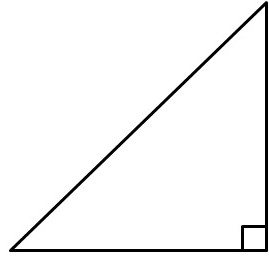
Boki trójkąta prostokątnego
Strona przeciwna pod kątem dziewięćdziesięciu stopni nazywana jest przeciwprostokątną. Pozostałe dwie strony nazywane są nogami. Przeciwprostokąt jest zawsze dłuższy niż nogi, ale krótszy niż ich suma.
Trójkąt prostokątny. Właściwości trójkąta
Jeśli noga jest przeciwległa do kąta trzydziestu stopni, wówczas jej długość odpowiada połowie długości przeciwprostokątnej. Wynika z tego, że kąt przeciwny do nogi, której długość odpowiada połowie przeciwprostokątnej, wynosi trzydzieści stopni. Noga jest równa proporcjonalnej przeciwprostokątnej i projekcji, którą noga podaje przeciwprostokątnej.
Twierdzenie Pitagorasa
Każdy trójkąt prostokątny jest zgodny z twierdzeniem Pitagorasa. Twierdzenie to stwierdza, że suma kwadratów nóg jest równa kwadratowi przeciwprostokątnej. Jeśli założymy, że nogi są a i b, a przeciwprostokątna to c, to piszemy: a 2 + 2 = c 2 . Twierdzenie Pitagorasa służy do rozwiązania wszystkich problemów geometrycznych, w których pojawiają się trójkąty prostokątne. Pomaga również narysować kąt prosty pod nieobecność niezbędnych narzędzi.
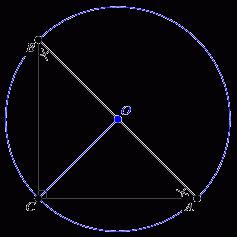
Wzrost i mediana
Prawy trójkąt charakteryzuje się tym, że jego dwie wysokości są połączone z nogami. Aby znaleźć osobę trzecią, musisz znaleźć sumę rzutów nóg na przeciwprostokątnej i podzielić przez dwa. Jeśli z wierzchołka pod kątem prostym do utrzymania mediany, wówczas będzie to promień okręgu, który jest opisany wokół trójkąta. Środek tego okręgu będzie środkiem przeciwprostokątnej.
Trójkąt prostokątny. Obszar i jego obliczenia
Obszar trójkątów prostych oblicza się za pomocą dowolnej formuły do znalezienia kwadratowy trójkąt. Dodatkowo możesz użyć innej formuły: S = a * b / 2, która mówi, że aby znaleźć obszar, musisz podzielić długość nóg na dwie nogi.
Cosinus, sinus i styczna trójkąta prostokątnego
Cosinus o kącie ostrym odnosi się do ustawienia nóg sąsiadujących z kątem do przeciwprostokątnej. Zawsze jest mniej niż jeden. Sinus to stosunek nogi, która znajduje się naprzeciwko narożnika, do przeciwprostokątnej. Styczna - stosunek nogi, która znajduje się naprzeciw rogu, do nogi, sąsiadującej z tym kątem. Cotangens to proporcja nogi sąsiadującej z rogiem, do nogi przeciwnej do rogu. Cosinus, sinus, styczna i cotangens nie zależą od wielkości trójkąta. Na ich wartość wpływa jedynie miara kąta.
Rozwiązanie trójkąta
Aby obliczyć wartość nogi, przeciwnie do kąta, pomnóż długość przeciwprostokątnej przez sinus tego kąta lub wielkość drugiej nogi przez styczną kąta. Aby znaleźć nogę przylegającą do narożnika, konieczne jest obliczenie iloczynu przeciwprostokątnego przez cosinus kąta.
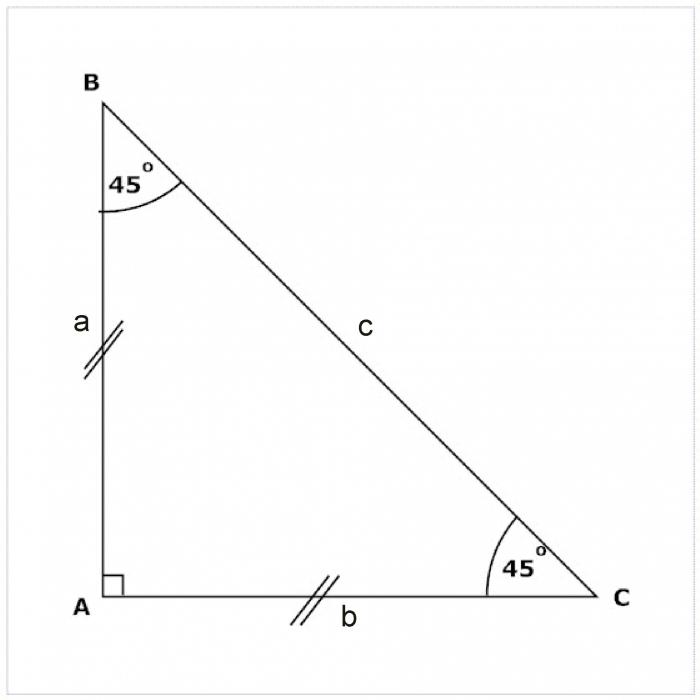
Trójkąt równoramienny
Jeśli trójkąt ma kąt prosty i równe, to nazywany jest trójkątem równoramiennym równoramiennym. Kąty ostre takiego trójkąta są równe - po 45 o. Mediana, dwusieczna i wysokość narysowana pod kątem prostym trójkąta równoramiennego pokrywają się.