Ruch obrotowy i prędkość kątowa ciała stałego
W tym artykule omówimy wielkości fizyczne, które charakteryzują ruch obrotowy ciała: prędkość kątową, przesunięcie kątowe, przyspieszenie kątowe, moment obrotowy.
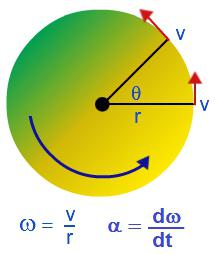
Sztywne ciało to zbiór sztywno połączonych punktów materialnych. Gdy ciało stałe obraca się wokół dowolnej osi, poszczególne punkty materialne, z których są dodawane, poruszają się po okręgach o różnych promieniach.
Przez pewien czas, na przykład, podczas którego ciało wykonuje jeden obrót, oddzielne punkty materialne, które tworzą ciało stałe, przechodzą różne ścieżki, dlatego oddzielne punkty będą miały różne prędkości liniowe. Opisz rotację bryły za pomocą prędkości liniowych jednostki istotne punkty - trudne.
Kątowe przemieszczenie
Jednak analizując ruch poszczególnych punktów materialnych, można ustalić, że w tym samym czasie wszystkie obracają się wokół osi pod tym samym kątem. Oznacza to, że aby opisać obrót bryły, wygodne jest użycie takiej wielkości fizycznej, jak kątowe przesunięcie:
φ = φ (t).
Prędkość kątowa i przyspieszenie kątowe
Ruch obrotowy można scharakteryzować za pomocą prędkości kątowej: ω = Δφ / Δt.
Prędkość kątowa charakteryzuje prędkość obrotu ciała i jest równa stosunkowi zmiany kąta obrotu do czasu, w którym nastąpiło. Mierzone w radianach na sekundę: [ω] = rad / s.
Prędkość kątowa obrotu jest zależna od prędkości liniowej przez następującą relację: v = Rω, gdzie R jest promieniem okręgu, wzdłuż którego porusza się ciało.
Ruch obrotowy ciało charakteryzuje się inną wielkością fizyczną - przyspieszenie kątowe, które jest równe stosunkowi zmiany prędkości kątowej do czasu, w którym miało miejsce: ε = Δω / Δt. Jednostka miary przyspieszenia kątowego: [ε] = rad / s 2 .
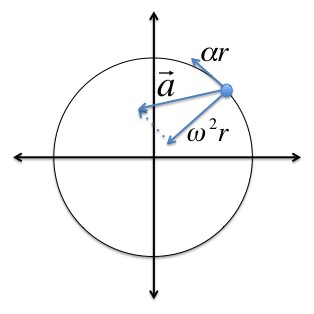
Prędkość kątowa i przyspieszenie kątowe są pseudowektorami, których kierunek zależy od kierunku obrotu. Można to określić za pomocą reguły właściwej śruby.
Jednolity ruch obrotowy
Równomierny ruch obrotowy odbywa się ze stałą prędkością kątową i jest opisany przez następujące równania: ε = 0, ω = const, φ = φ 0 + ωt, gdzie φ 0 jest początkową wartością kąta obrotu.
Równomiernie przyspieszony ruch obrotowy
Równomiernie przyspieszony ruch obrotowy występuje przy stałym przyspieszeniu kątowym i jest opisany przez następujące równania: ε = const, ω = ω 0 + εt, φ = φ 0 + ω 0 t + εt 2/2.
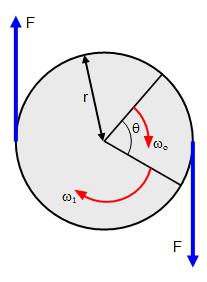
Podczas obracania bryły przyspieszenie dośrodkowe każdy punkt tego ciała można znaleźć w następujący sposób: ɑ c = v 2 / R = (ωR) 2 / R = ω 2 R.
Po przyspieszeniu obrotu bryły można znaleźć przyspieszenie styczne jej punktów za pomocą wzoru: ɑ t = Δv / Δt = Δ (ωR) / Δt = R (Δω / Δt) = Rε.
Moment siły
Jeśli, biorąc pod uwagę problem fizyczny, mamy do czynienia nie z punktem materialnym, ale z ciałem stałym, to działanie kilku sił na niego zastosowane do różnych punktów tego ciała nie może być zredukowane do działania pojedynczej siły. W takim przypadku rozważ moment sił.
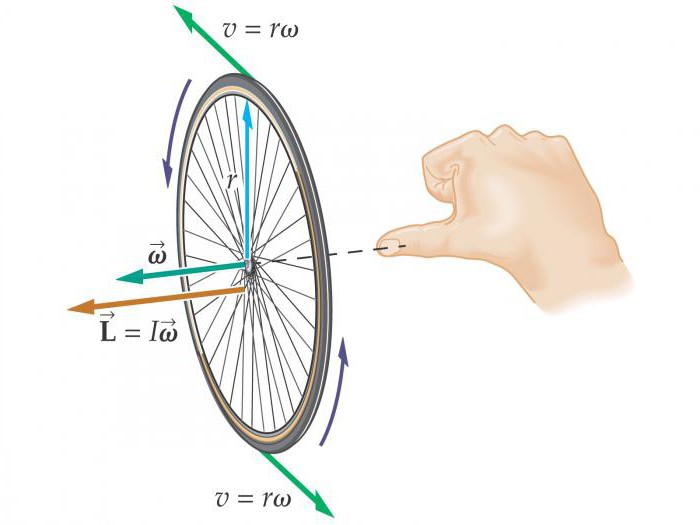
Moment siły nazywa się siłą na ramieniu. Jest to wielkość wektorowa i znajduje się za pomocą wzoru: M = RFsinα, gdzie α to kąt między wektorami R i F. Jeśli istnieje kilka momentów sił działających na ciało, wtedy ich działanie można zastąpić ich wypadkową, sumą wektorową tych momentów: M = M 1 + M 2 + ... + M n .
Eksperymenty i doświadczenie pokazują, że pod wpływem chwili siły zmienia się prędkość kątowa ciała, to znaczy ciało ma akcelerację kątową. Zobaczmy, w jaki sposób przyspieszenie kątowe punktu materialnego (zbioru punktów materialnych) zależy od przyłożonego momentu obrotowego: F = mɑ, RF = Rma = R 2 mβ, β = M / mR 2 = M / I, gdzie I = mR 2 to moment bezwładności materiału punkty. Należy zauważyć, że moment bezwładności ciała zależy zarówno od masy ciała, jak i umiejscowienia tej masy względem osi obrotu.
Przykłady rozwiązywania problemów
Zadanie 1. Wirnik wirnika wytwarza 2 • 10 4 rpm. Po wyłączeniu silnika jego obrót zatrzymuje się po 8 minutach. Znajdź przyspieszenie kątowe, a także liczbę obrotów wirnika od momentu wyłączenia silnika aż do zatrzymania, biorąc pod uwagę, że ruch wirnika jest równomiernie przyspieszany.
Rozwiązanie
Znajdźmy przyspieszenie kątowe, biorąc pod uwagę, że prędkość kątowa z równomiernie przyspieszonym ruchem jest opisana równaniem: ω (t) = ω 0 - εt.
Stąd, biorąc pod uwagę, że na końcu ruchu prędkość wynosi zero, stwierdzamy: ε = ω 0 / t = 2nn / t.
Przeniesienie tych zadań do jednostek SI jednostek (n = 333 obr / s, t = 480 s) , otrzymujemy: ε = 2π333 / 480 = 4,36 (rad / s 2 ).
Kąt obrotu rotora wirówki podczas czasu t będzie wynosił : φ (t) = φ 0 + ω 0 t + εt 2/2. Y odczytując wyrażenie przyspieszenia kątowego i fakt, że φ 0 = 0 , znajdujemy: φ (t) = ω 0 t / 2 = πnt.
Liczba obrotów wirnika w tym czasie będzie wynosić: N = φ (t) / 2π = πnt / 2π = nt = 8 • 10 4 (vol.).
Odpowiedź: przyspieszenie kątowe wynosi 4,36 rad / s 2 ; liczba obrotów wirnika od momentu wyłączenia silnika aż do całkowitego zatrzymania wynosi 8 • 10 4 obr / min.
Zadanie 2. Dysk o masie 1 kg i promieniu 20 cm obraca się z częstotliwością 120 obrotów na minutę za minutę. Pod działaniem urządzenia hamulcowego na krawędzi dysku zaczęło działać siła tarcia 10 N. Znajdź czas na zatrzymanie dysku, po tym jak zacznie działać siła tarcia.
Rozwiązanie
Znajdź moment hamowania działający na tarczę: M = RF.
Znajdź przyspieszenie kątowe dysku: ε = M / I = FR / mR 2 = F / mR.
Znajdźmy czas, w którym dysk się zatrzyma: t = ω 0 / ε , gdzie ω 0 to początkowa prędkość kątowa dysku, która jest równa 2πv.
Wykonujemy obliczenia: t = 2πv / ε = 2πvmR / F = 6,28 • 2 • 1 • 0,2 / 10 = 2,5 (s).
Odpowiedź: czas zatrzymania wynosi 2,5 sekundy.