Historia twierdzenia Pitagorasa. Dowód twierdzenia
Ci, którzy interesują się historią twierdzenia Pitagorasa, która jest studiowana w szkolnym programie nauczania, będą również ciekawi, że w 1940 r. Opublikowana zostanie książka z trzystoma siedmioma dowodami tego pozornie prostego twierdzenia. Intrygowała jednak umysły wielu matematyków i filozofów różnych epok. W Księdze Rekordów Guinnessa jest to ustalone jako twierdzenie z maksymalną liczbą dowodów.
Historia twierdzenia Pitagorasa
Powiązany z nazwą Pitagorasa, twierdzenie było znane na długo przed narodzinami wielkiego filozofa. Tak więc w Egipcie podczas konstruowania struktur wzięto pod uwagę proporcje trójkąta prostokątnego sprzed pięciu tysięcy lat. Teksty babilońskie odnoszą się do tego samego współczynnika kształtu. trójkąt prostokątny 1200 lat przed narodzinami Pitagorasa.
Ad

Nasuwa się pytanie, dlaczego więc historia mówi - należy do niego powstanie twierdzenia Pitagorasa? Odpowiedź może być tylko jedna - udowodnił proporcje w trójkącie. Robił to, co przed wiekami ci, którzy po prostu używali współczynnika kształtu, a przeciwprostokątna ustalona empirycznie nie zrobiła tego.
Z życia Pitagorasa
Przyszłość świetna naukowiec, matematyk, Filozof urodził się na wyspie Samos w 570 roku pne. W dokumentach historycznych przechowywano informacje o ojcu Pitagorasa, który był rzeźbiarzem kamieni szlachetnych, ale nie ma informacji o matce. Mówiono o chłopcu, który urodził się, że był niezwykłym dzieckiem, które od dzieciństwa wykazywało pasję do muzyki i poezji. Historycy przypisują nauczycielom młodego Pitagorasa do Herdomadant i Feryid z Syros. Pierwszy wprowadził chłopca w świat muz, a drugi, będąc filozofem i założycielem włoskiej szkoły filozofii, skierował spojrzenie młodzieńca w stronę logosu.
Ad
W wieku 22 lat (548 pne, E.) Pitagoras udał się do Nookratis, aby studiować język i religię Egipcjan. Co więcej, jego droga była w Memfis, gdzie dzięki kapłanom, po przejrzeniu ich genialnych prób, zrozumiał egipską geometrię, która być może skłoniła dociekliwego młodzieńca do udowodnienia twierdzenia Pitagorasa. Historia przypisze to twierdzenie do twierdzenia w przyszłości.

Schwytany przez króla Babilonu
W drodze do domu do Hellady Pythagoras zostaje schwytany przez króla Babilonu. Ale bycie w niewoli przyniosło korzyści dociekliwemu umysłowi początkującego matematyka, musiał się czegoś nauczyć. Rzeczywiście, w tamtych latach matematyka w Babilonie była bardziej rozwinięta niż w Egipcie. Spędził dwanaście lat na studiowaniu matematyki, geometrii i magii. I prawdopodobnie była to geometria babilońska, która była zaangażowana w dowód proporcji trójkąta i historię odkrycia twierdzenia. Pitagoras miał wystarczającą wiedzę i czas na to. Ale tak się stało w Babilonie, nie ma potwierdzenia dokumentu ani obalenia.
W 530 pne Pitagoras ucieka z niewoli do swojej ojczyzny, gdzie mieszka na dworze tyrana Polikratesa w statusie półpłyta. Takie życie nie pasuje do Pitagorasa, a on wycofuje się do jaskiń Samos, a następnie udaje się na południe Włoch, gdzie znajdowała się grecka kolonia Croton.
Tajny porządek monastyczny
Na podstawie tej kolonii Pitagoras zorganizował tajny porządek monastyczny, który był jednocześnie związkiem religijnym i społeczeństwem naukowym. Społeczeństwo to miało swój własny statut, który odnosił się do przestrzegania określonego sposobu życia.
Ad

Pitagoras twierdził, że aby zrozumieć Boga, człowiek musi uczyć się takich nauk jak algebra i geometria, znać astronomię i rozumieć muzykę. Praca badawcza została zredukowana do znajomości mistycznej strony liczb i filozofii. Należy zauważyć, że zasady głoszone przez Pitagorasa w tym czasie mają na razie sens w naśladowaniu.
Wiele z tych odkryć dokonanych przez uczniów Pitagorasa zostało mu przypisanych. Niemniej jednak, jeśli mówić krótko, historia powstania twierdzenia Pitagorasa przez starożytnych historyków i biografów tamtych czasów, wiąże się bezpośrednio z nazwiskiem tego filozofa, myśliciela i matematyka.
Nauki Pitagorasa
Być może myśl o połączeniu twierdzenia z nazwą Pitagorasa skłoniła historyków do powiedzenia wielkiego greka, że wszystkie zjawiska naszego życia są zakodowane w notorycznym trójkącie z jego nogami i przeciwprostokątną. A ten trójkąt jest "kluczem" do rozwiązania wszystkich pojawiających się problemów. Wielki filozof powiedział, że należy zobaczyć trójkąt, wtedy możemy założyć, że problem rozwiązano w dwóch trzecich.

Pitagoras mówił o swojej nauce tylko werbalnie do swoich uczniów, nie robiąc żadnych notatek, utrzymując to w tajemnicy. Niestety, nauki największego filozofa nie przetrwały do dziś. Coś z niego wyciekło, ale nie można powiedzieć, ile jest prawdą, a ile jest fałszywe w tym, co stało się znane. Nawet z historią twierdzenia Pitagorasa nie wszystkie są niepodważalne. Historycy matematyki wątpią w autorstwo Pitagorasa, ich zdaniem twierdzenie zostało użyte wiele wieków przed jego narodzinami.
Twierdzenie Pitagorasa
Może wydawać się to dziwne, ale nie ma historycznych dowodów twierdzenia samego Pitagorasa - ani w archiwach, ani w żadnym innym źródle. We współczesnej wersji uważa się, że nie należy on do nikogo innego, jak sam Euklides.
Ad
Istnieją dowody na to, że jeden z największych historyków matematyki, Moritz Cantor, odkrył na papirusie przechowywanym w Muzeum Berlińskim, zarejestrowanym przez Egipcjan w około 2300 r. Pne. e. równość, która brzmi: 3² + 4² = 5².
Krótko z historii twierdzenia Pitagorasa
Formułowanie twierdzenia z "zasad" euklidesowej w tłumaczeniu brzmi tak samo, jak we współczesnej interpretacji. Nie ma w nim nowego odczytu: kwadrat strony przeciwnej do kąta prostego jest równy sumie kwadratów boków sąsiadujących z kątem prostym. Fakt, że starożytne cywilizacje Indii i Chin używały twierdzenia, potwierdza traktat Zhou - bi suan jin. Zawiera informacje o egipskim trójkącie, który opisuje proporcje jako 3: 4: 5.

Nie mniej interesująca jest inna chińska książka matematyczna, Chu-Pei, która również wspomina o trójkącie pitagorejskim z wyjaśnieniem i rysunkami, które pokrywają się z rysunkami hinduskiej geometrii Bashary. O samym trójkącie w książce napisano, że jeśli kąt prosty może zostać rozłożony na części składowe, wówczas linia łącząca końce boków będzie równa pięciu, jeśli podstawa ma trzy, a wysokość cztery.
Indyjski traktat "Sulva Sutra", którego historia sięga VII-V wieku pne. e. mówi o budowaniu kąta prostego za pomocą trójkąta egipskiego.
Dowód twierdzenia
W średniowieczu uczniowie uważali dowód twierdzenia za zbyt trudny. Słabi uczniowie na pamięć zapamiętali twierdzenia, nie rozumiejąc znaczenia dowodu. W związku z tym otrzymali przydomek "osły", ponieważ twierdzenie Pitagorasa stanowiło dla nich przeszkodę nie do pokonania, jak most na osła. W średniowieczu uczniowie wymyślili żartobliwy werset na temat tego twierdzenia.
Ad
Aby udowodnić twierdzenie Pitagorasa w najprostszy sposób, należy po prostu zmierzyć jego boki, bez użycia koncepcji kwadratów w dowodzie. Długość boku przeciwległego do kąta prostego to c, a sąsiednie a i b, w wyniku czego otrzymujemy równanie: a 2 + b 2 = c 2 . To stwierdzenie, jak wspomniano powyżej, jest weryfikowane przez pomiar długości boków trójkąta prostokątnego.
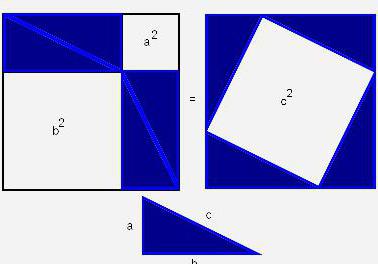
Jeśli zaczniemy dowód twierdzenia, biorąc pod uwagę obszar prostokątów zbudowanych na bokach trójkąta, możemy określić obszar całej figury. Będzie równy powierzchni kwadratu z bokiem (a + b), az drugiej strony sumą powierzchni czterech trójkątów i kwadratu wewnętrznego.
(a + b) 2 = 4 x ab / 2 + c 2 ;
a 2 + 2ab + b 2 ;
c 2 = a 2 + b 2 , zgodnie z wymaganiami.
Praktyczne znaczenie twierdzenia Pitagorasa polega na tym, że można go wykorzystać do określenia długości segmentów bez ich pomiaru. Podczas budowy budynków obliczane są odległości, położenie podpór i belek, wyznaczane są środki ciężkości. Twierdzenie Pitagorasa stosuje się we wszystkich nowoczesnych technologiach. Nie zapominaliśmy o twierdzeniu przy tworzeniu filmów w wymiarach 3D-6D, gdzie oprócz 3 standardowych wartości: wysokość, długość, szerokość - czas, zapach i smak są brane pod uwagę. Jakie są smaki i zapachy związane z twierdzeniem - pytasz? To bardzo proste - kiedy pokazujesz film, musisz obliczyć, gdzie i co pachnie i smakuje, aby wysłać go do audytorium.
Czy nadal będzie. Nieograniczona przestrzeń do odkrywania i tworzenia nowych technologii czeka na dociekliwych umysły.