Rzut punktu na płaszczyźnie. Rzut punktu na linii prostej w płaszczyźnie
Badanie właściwości figur w przestrzeni i na płaszczyźnie jest niemożliwe bez znajomości odległości między punktem a takimi obiektami geometrycznymi, jak linia prosta i płaszczyzna. W tym artykule pokażemy, jak znaleźć te odległości, biorąc pod uwagę rzut punktu na płaszczyznę i na linię prostą.
Równanie linii dla przestrzeni dwuwymiarowych i trójwymiarowych
Obliczanie odległości punktu do linii prostej i płaszczyzny odbywa się za pomocą rzutowania na te obiekty. Aby móc znaleźć te projekcje, należy wiedzieć, w jakiej formie podane są równania linii prostych i płaszczyzn. Zacznijmy od pierwszego.
Linia prosta to zbiór punktów, z których każdy można uzyskać od poprzedniego, przenosząc do wektorów równoległych. Na przykład, istnieje punkt M i N. Wektor łączący je MN¯ przyjmuje od M do N. Istnieje również trzeci punkt P. Jeśli wektor MP¯ lub NP¯ jest równoległy do MN¯, wówczas wszystkie trzy punkty na jednej linii leżą i tworzą je.
W zależności od wymiaru przestrzeni równanie definiujące linię może zmienić jej kształt. Zatem dobrze znana liniowa zależność współrzędnej y na x w przestrzeni opisuje płaszczyznę, która jest równoległa do trzeciej osi z. W związku z tym w tym artykule rozważymy tylko równanie wektorowe dla linii. Ma taki sam wygląd dla płaszczyzny i trójwymiarowej przestrzeni.
W przestrzeni linia prosta może być zdefiniowana następującym wyrażeniem:
(x; y; z) = (x 0 ; y 0 ; z 0 ) + α * (a; b; c)
W tym przypadku wartości współrzędnych z zerowymi wskaźnikami odpowiadają linii prostej należącej do pewnego punktu, u¯ (a; b; c) jest współrzędną wektora kierującego, który leży na danej linii prostej, α jest dowolną liczbą rzeczywistą, zmieniającą się, które można uzyskać wszystkie punkty linii prostej. To równanie nazywa się wektorem.
Często powyższe równanie jest napisane w formie otwartej:
x = x 0 + a * a;
y = y 0 + α * b;
z = z 0 + α * c
Podobnie, możemy zapisać równanie prostej w płaszczyźnie, to znaczy w przestrzeni dwuwymiarowej:
(x; y) = (x 0 ; y 0 ) + α * (a; b);
x = x 0 + a * a;
y = y 0 + α * b
Równanie płaszczyzny
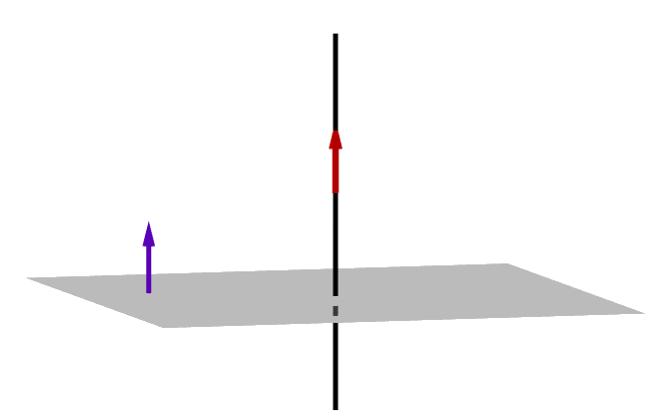
Aby móc znaleźć odległość od punktu do płaszczyzn rzutów, musisz wiedzieć, jak definiuje się płaszczyznę. Podobnie jak linia prosta, może być reprezentowana na kilka sposobów. Rozważamy tylko jeden: ogólne równanie.
Załóżmy, że punkt M (x 0 ; y 0 ; z 0 ) należy do płaszczyzny, a wektor n ¯ (A; B; C) jest do niego prostopadły, a następnie dla wszystkich punktów (x; y; z) płaszczyzny, następująca równość będzie prawdziwa:
A * x + B * y + C * z + D = 0, gdzie D = -1 * (A * x 0 + B * y 0 + C * z 0 )
Należy pamiętać, że w tym ogólnym równaniu płaszczyzny współczynniki A, B i C są współrzędnymi normalnej do płaszczyzny wektora.
Obliczanie odległości za pomocą współrzędnych
Przed przystąpieniem do rozważań na temat rzutów na płaszczyźnie punktu i linii prostej, należy przypomnieć, jak obliczyć odległość między dwoma znanymi punktami.
Załóżmy, że istnieją dwa punkty przestrzenne:
A 1 (x 1 ; y 1 ; z 1 ) i A 2 (x 2 ; y 2 ; z 2 )
Wtedy odległość między nimi jest obliczana według wzoru:
A 1 A 2 = √ (((x 2- x 1 ) 2 + (y 2 -y 1 ) 2 + (z 2 -z 1 ) 2 )
Za pomocą tego wyrażenia określa się również długość wektora A 1 A 2 ¯.
Dla przypadku w płaszczyźnie, gdy podane są dwa punkty z parą współrzędnych, możesz napisać podobne równanie bez obecności elementu z, w którym:
A 1 A 2 = √ (((x 2- x 1 ) 2 + (y 2 -y 1 ) 2 )
Teraz rozważymy różne przypadki rzutowania na płaszczyźnie punktu na linii prostej i na płaszczyźnie w przestrzeni.
Punkt, linia i odległość między nimi
Załóżmy, że istnieje punkt i prosta:
P 2 (x 1 ; y 1 );
(x; y) = (x 0 ; y 0 ) + α * (a; b)
Odległość między tymi obiektami geometrycznymi odpowiada długości wektora, którego początek leży w punkcie P 2 , a koniec znajduje się w takim punkcie P na wskazanej linii prostej, dla którego wektor P 2 P ¯ tej prostej jest prostopadły. Punkt P nazywany jest rzutem punktu P2 na daną linię.
Poniższy rysunek pokazuje punkt P 2 , odległość d do linii prostej, a także wektor kierunku v 1 ¯. Również na linii wybierany jest dowolny punkt P 1, a wektor jest od niego pobierany do P 2 . Punkt P tutaj pokrywa się z miejscem, w którym prostopadła przecina linię.
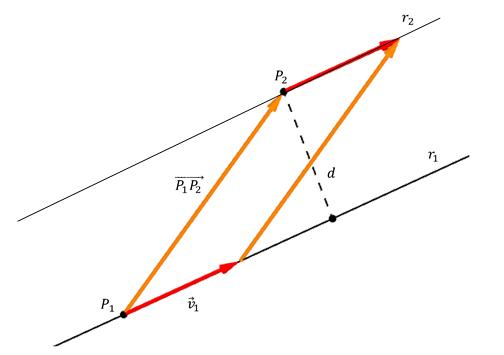
Widać, że pomarańczowe i czerwone strzałki tworzą równoległobok, którego bokami są wektory P1 P 2 ¯ i v 1 ¯, a wysokość to d. Z geometrii wiadomo, że aby znaleźć wysokość równoległoboku, jego powierzchnię należy podzielić przez długość podstawy, na której prostopadła jest obniżona. Ponieważ powierzchnia równoległoboku jest obliczana jako iloczyn wektorowy jego boków, otrzymujemy wzór do obliczenia d:
d = | [P 1 P 2 ¯ * v 1 ¯] | / | v 1 ¯ |
Wszystkie wektory i współrzędne punktów w tym wyrażeniu są znane, więc można go używać bez wykonywania żadnych transformacji.
Możliwe byłoby rozwiązanie tego problemu w inny sposób. Aby to zrobić, zapisz dwa równania:
- iloczyn skalarny P 2 P ¯ na v 1 ¯ powinien być równy zeru, ponieważ wektory te są wzajemnie prostopadłe;
- współrzędne punktu P muszą spełniać równanie linii.
Równania te wystarczają do znalezienia współrzędnych P, a następnie długości d według wzoru podanego w poprzednim akapicie.
Zadanie znalezienia odległości między linią a punktem
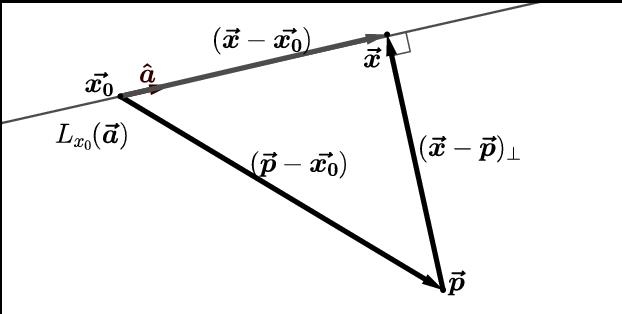
Pokazujemy, jak wykorzystać te teoretyczne informacje do rozwiązania konkretnego problemu. Załóżmy, że następujący punkt i linia są znane:
M (5; -3);
(x; y) = (3; 1) - α * (0; 2)
Konieczne jest znalezienie punktów rzutowania na linii prostej na płaszczyźnie, a także odległości od M do linii prostej.
Oznaczenie rzutu znalezionego przez punkt M 1 (x 1 ; y 1 ). Rozwiązujemy ten problem na dwa sposoby, opisane w poprzednim akapicie.
Metoda 1. Współrzędne wektora kierunku 1 has wynoszą (0; 2). Aby zbudować równoległobok, wybierz punkt należący do linii prostej. Na przykład punkt o współrzędnych (3; 1). Następnie wektor drugiej strony równoległoboku będzie miał współrzędne:
(5; -3) - (3; 1) = (2; -4)
Teraz należy obliczyć iloczyn wektorów definiujących boki równoległoboku:
[(2; -4) * (0; 2)] = 4
Zamienimy tę wartość na formułę, otrzymujemy odległość d od M do linii prostej:
d = 4 / √ 4 = 2
Metoda 2. Teraz znajdziemy w inny sposób nie tylko odległość, ale także współrzędne rzutu M na linii, zgodnie z warunkiem stanu problemu. Jak wspomniano powyżej, aby rozwiązać problem, konieczne jest stworzenie systemu równań. Ona będzie wyglądać jak:
(x 1 -5) * 0 + (y 1 + 3) * 2 = 0;
(x 1 ; y 1 ) = (3; 1) -α * (0; 2)
Rozwiązujemy ten system:
y 1 = -3;
x 1 = 3
Rzutem punktu początkowego współrzędnej jest M 1 (3; -3). Wymagana odległość to:
d = | MM 1 ¯ | = √ (4 + 0) = 2
Jak widać, oba rozwiązania dały taki sam wynik, który wskazuje na poprawność wykonanych operacji matematycznych.
Projekcja punktu w płaszczyźnie
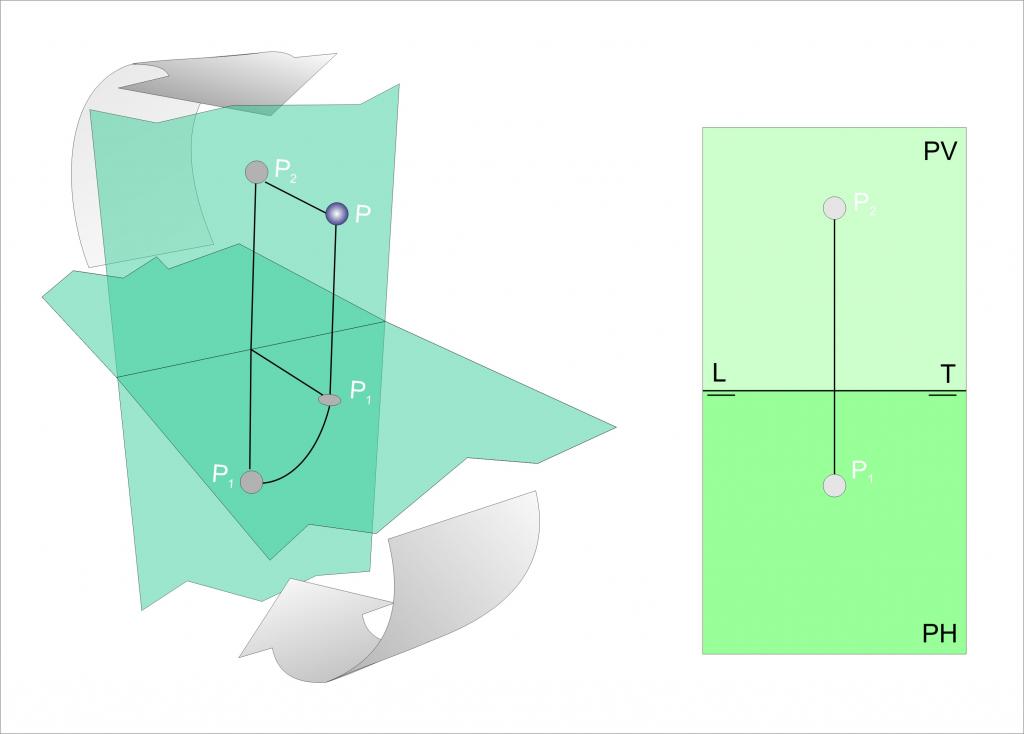
Teraz zastanówcie się, jaka jest projekcja punktu podanego w przestrzeni na określonej płaszczyźnie. Łatwo zgadnąć, że ten występ jest również punktem, który wraz z pierwotnym tworzy wektor prostopadły do płaszczyzny.
Załóżmy, że rzutowanie na płaszczyźnie współrzędnych punktu M ma następującą postać:
M 1 (x 1 ; y 1 ; z 1 )
Sam samolot jest opisany przez równanie:
A * x + B * y + C * z + D = 0
Na podstawie tych danych możemy wykonać równanie prostej przecinającej płaszczyznę pod kątem prostym i przechodzącej przez M i M 1 :
(x; y; z) = (x 0 ; y 0 ; z 0 ) + α * (A; B; C)
Tutaj zmienne z zerowymi wskaźnikami są współrzędnymi punktu M. Położenie na płaszczyźnie punktu M 1 można obliczyć na tej podstawie, że jego współrzędne muszą spełniać oba zapisane równania. Jeśli te równania nie są wystarczające do rozwiązania problemu, można zastosować warunek równoległości MM 1 ¯ i wektor kierunkowy dla danej płaszczyzny.
Oczywiście rzut punktu należącego do płaszczyzny pokrywa się z samym sobą, a odpowiednia odległość wynosi zero.
Zadanie z punktem i płaszczyzną
Niech dany punkt M (1; -1; 3) i płaszczyzna, która jest opisana następującym ogólnym równaniem:
-x + 3 * y -2 * z + 4 = 0
Konieczne jest obliczenie współrzędnych rzutu na płaszczyźnie punktu i obliczenie odległości między tymi obiektami geometrycznymi.
Na początek skonstruujemy równanie linii przechodzącej przez M i prostopadłej do wskazanej płaszczyzny. Wygląda to tak:
(x; y; z) = (1; -1; 3) + α * (- 1; 3; -2)
Oznacz punkt, w którym ta prosta przecina płaszczyznę M 1 . Równości dla samolotu i linii prostej muszą być spełnione, jeśli zastąpimy w nich współrzędne M 1 . Pisząc w formie jawnej równanie prostej, otrzymujemy następujące cztery równania:
-x 1 + 3 * y 1 -2 * z 1 + 4 = 0;
x 1 = 1 - α;
y 1 = -1 + 3 * α;
z 1 = 3 - 2 * α
Z ostatniej równości otrzymujemy parametr α, a następnie zastępujemy go w przedostatnim i drugim wyrażeniu, otrzymujemy:
α = (3-z 1 ) / 2;
y 1 = -1 + 3 * (3-z 1 ) / 2 = -3 / 2 * z 1 + 3,5;
x 1 = 1 - (3-z 1 ) / 2 = 1/2 * z 1 - 1/2
Wyrażenie dla y 1 i x 1 jest podstawione do równania dla płaszczyzny, mamy:
-1 * (1/2 * z 1 - 1/2) + 3 * (- 3/2 * z 1 + 3,5) -2 * z 1 + 4 = 0
Gdzie otrzymamy:
z 1 = 15/7
Następnie:
y 1 = -3 / 2 * 15/7 + 3,5 = 2/7;
x 1 = 1/2 * 15/7 - 1/2 = 4/7
Ustaliliśmy, że rzut punktu M na danej płaszczyźnie odpowiada współrzędnym (4/7, 2/7, 15/7).
Teraz obliczyć odległość | MM 1 ¯ |. Współrzędne odpowiedniego wektora to:
MM 1 ¯ (-3/7; 9/7; -6/7)
Wymagana odległość to:
d = | MM 1 ¯ | = √126 / 7 ≈ 1.6
Trzy punkty projekcyjne
Podczas wytwarzania rysunków często konieczne jest uzyskanie rzutów przekrojów na wzajemnie prostopadłych trzech płaszczyznach. Dlatego warto zastanowić się, co będzie rzutować na projekcje pewnego punktu M o współrzędnych (x 0 ; y 0 ; z 0 ) na trzy płaszczyzny współrzędnych.

Nie jest trudno pokazać, że płaszczyzna Xy jest opisana równaniem z = 0, płaszczyzna Xz odpowiada wyrażeniu y = 0, a pozostała płaszczyzna yz jest oznaczona przez równość x = 0. Łatwo zgadnąć, że rzuty punktu na 3 płaszczyznach będą równe:
dla x = 0: (0; y 0 ; z 0 );
dla y = 0: (x 0 ; 0; z 0 );
dla z = 0: (x 0 ; y 0 ; 0)
Gdzie jest ważne poznanie rzutów punktu i jego odległości od płaszczyzn?
Ustalenie położenia rzutów punktów na danej płaszczyźnie jest ważne przy znajdowaniu takich wielkości, jak powierzchnia i objętość dla ukośnych graniastosłupów i piramid. Na przykład odległość od wierzchołka piramidy do płaszczyzny podstawy to wysokość. Ten ostatni jest zawarty we wzorze na objętość tej liczby.
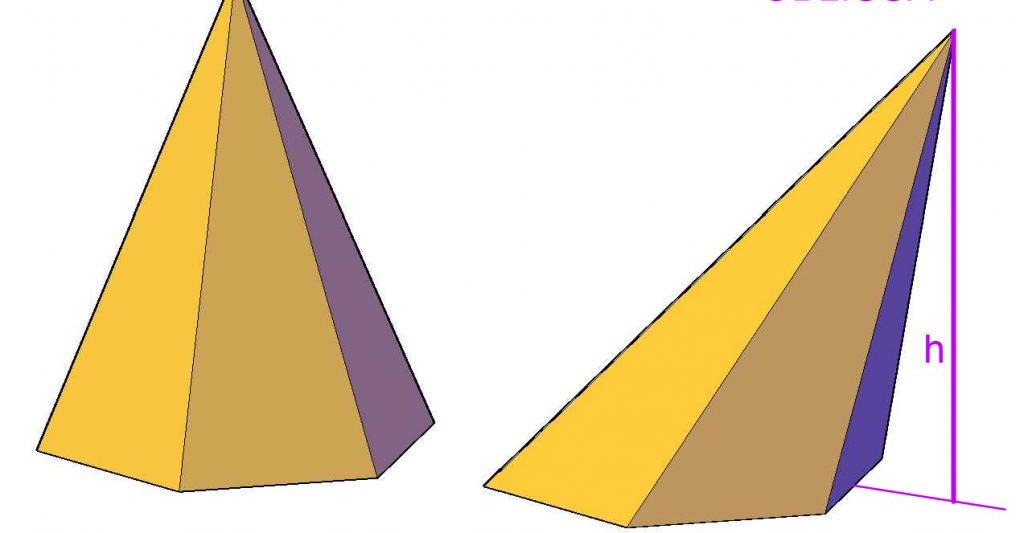
Rozważane formuły i metody określania rzutów i odległości od punktu do linii prostej i płaszczyzny są dość proste. Ważne jest, aby zapamiętać odpowiednie formy płaszczyzny i bezpośrednie równania, a także mieć dobrą wyobraźnię przestrzenną, aby z powodzeniem zastosować je.