Przestrzeń trójwymiarowa: wektory, współrzędne

Nawet od szkolnego kursu algebry i geometrii wiemy o koncepcji przestrzeni trójwymiarowej. Jeśli rozumieć, termin "przestrzeń trójwymiarowa" jest zdefiniowany jako układ współrzędnych z trzema wymiarami (wszyscy o tym wiedzą). W rzeczywistości możliwe jest opisanie dowolnego obiektu objętości za pomocą długości, szerokości i wysokości w klasycznym sensie. Jednak, powiedzmy, wykop trochę głębiej.

Czym jest przestrzeń trójwymiarowa

Jak już stało się jasne, zrozumienie trójwymiarowej przestrzeni i obiektów zdolnych do jej istnienia jest określone przez trzy główne pojęcia. To prawda, że ​​w przypadku punktu są to dokładnie trzy wartości, a w przypadku prostych, zakrzywionych, przerywanych linii lub obiektów objętościowych odpowiednie współrzędne mogą być większe.

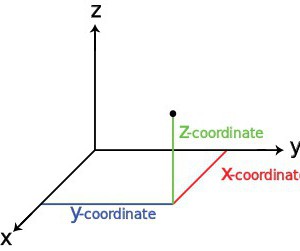
W tym przypadku wszystko zależy od rodzaju obiektu i zastosowanego układu współrzędnych. Dzisiaj system kartezjański, czasem nazywany również prostokątem, uważany jest za najbardziej powszechny (klasyczny). Ona i kilka innych gatunków zostaną omówione później.

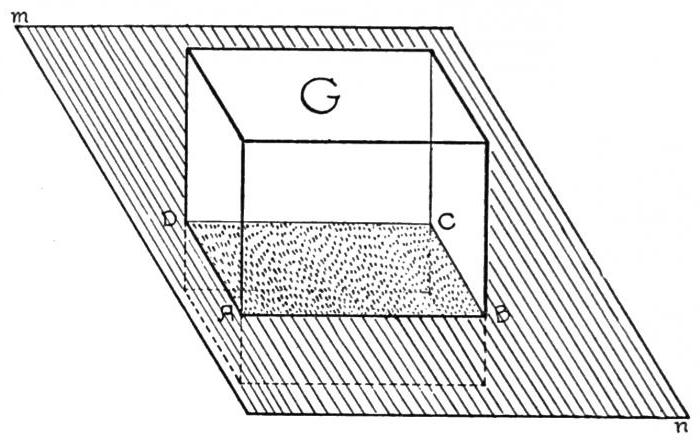
Między innymi tutaj trzeba rozróżnić pojęcia abstrakcyjne (jeśli to możliwe, bezkształtne), takie jak punkty, proste linie lub płaszczyzny i figury, które mają skończone wymiary, a nawet objętość. Dla każdej z tych definicji istnieją również własne równania opisujące ich możliwe położenie w przestrzeni trójwymiarowej. Ale teraz nie o to chodzi.

Pojęcie punktu w przestrzeni trójwymiarowej

Na początek definiujemy punkt w przestrzeni trójwymiarowej. Ogólnie można go nazwać pewną podstawową jednostką, która definiuje dowolną płaską lub trójwymiarową figurę, linię, segment, wektor, płaszczyznę itp.

Sam punkt charakteryzuje się trzema głównymi współrzędnymi. Dla nich w systemie prostokątnym stosowane są specjalne prowadnice, zwane osiami X, Y i Z, dwie pierwsze osie służące do wyrażania położenia poziomego obiektu, a trzecie odnosi się do pionowej specyfikacji współrzędnych. Oczywiście, dla wygody wyrażania położenia obiektu względem zerowych współrzędnych w systemie, przyjmuje się wartości dodatnie i ujemne. Jednak dzisiaj możesz znaleźć inne systemy.

Odmiany układów współrzędnych

Jak już wspomniano, prostokątny układ współrzędnych utworzony przez Kartezjusza jest dziś najważniejszy. Niemniej jednak w niektórych technikach określania położenia obiektu w przestrzeni trójwymiarowej stosuje się inne odmiany.

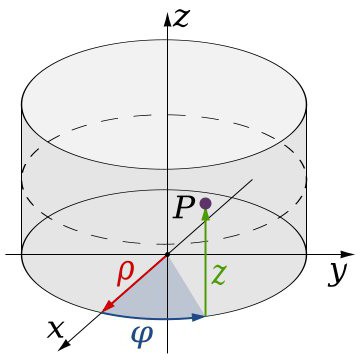
Najbardziej znane są systemy cylindryczne i sferyczne. Różnica w stosunku do klasycznego polega na tym, że podczas określania tych samych trzech wartości, które determinują położenie punktu w przestrzeni trójwymiarowej, jedna z wartości jest kątowa. Innymi słowy, w takich układach stosuje się okrąg odpowiadający kątowi 360 stopni. Odtąd i specyficzne zadanie współrzędnych, w tym takie elementy jak promień, kąt i tworzące. Współrzędne w trójwymiarowej przestrzeni (systemie) tego typu są posłuszne nieco innym prawom. Ich zadaniem w tym przypadku steruje zasada prawej ręki: jeśli połączysz kciuk i palec wskazujący z osiami X i Y, pozostałe palce w pozycji wygiętej będą wskazywać kierunek osi Z.

Pojęcie linii w przestrzeni trójwymiarowej

Teraz kilka słów o tym, co stanowi linię prostą w przestrzeni trójwymiarowej. W oparciu o podstawową koncepcję linii prostej jest to rodzaj nieskończonej linii przebiegającej przez punkt lub dwa, nie licząc zestawu punktów znajdujących się w sekwencji, która nie zmienia bezpośredniego przejścia przez nie linii.

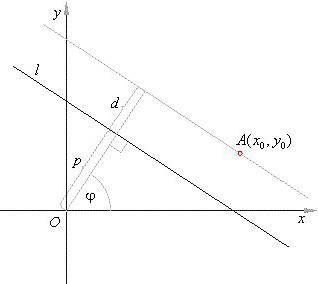
Jeśli spojrzysz na linię narysowaną przez dwa punkty w przestrzeni trójwymiarowej, będziesz musiał wziąć pod uwagę trzy współrzędne obu punktów. To samo dotyczy segmentów i wektorów. Te ostatnie określają podstawę trójwymiarowej przestrzeni i jej wymiaru.

Definicja wektorów i podstawa przestrzeni trójwymiarowej

Jak powszechnie wiadomo, w trójwymiarowym układzie współrzędnych mogą znajdować się trzy główne wektory, które definiują podstawę. Co więcej, zasady z odpowiednimi niezależnymi trzema wektorami mogą być niezliczone.

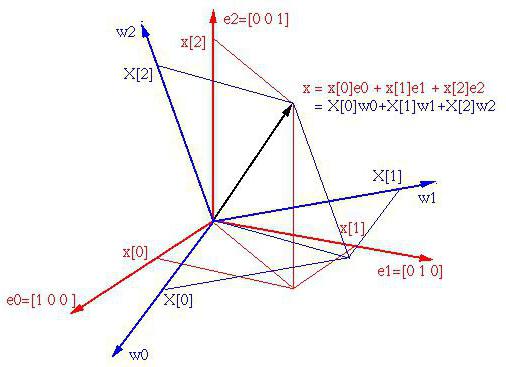
Zauważ, że mogą być tylko trzy wektory, ale tutaj możesz zdefiniować aż trzy trójek wektorów. Wymiar przestrzeni jest określony przez liczbę liniowo niezależnych wektorów (w naszym przypadku trzy). A przestrzeń, w której istnieje skończona liczba takich wektorów, nazywana jest skończonością.

Wektory zależne i niezależne

Jeśli chodzi o definicję wektorów zależnych i niezależnych, wektory, które są rzutami (na przykład, wektory osi X rzutowane na osi Y) są uważane za liniowo niezależne.

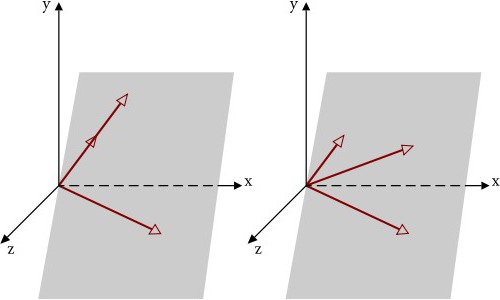
Jak już wiadomo, czwarty wektor jest zależny (teoria przestrzeni liniowych). Ale trzy niezależne wektory w przestrzeni trójwymiarowej nie muszą koniecznie leżeć w tej samej płaszczyźnie. Ponadto, jeśli zdefiniujemy niezależne wektory w przestrzeni trójwymiarowej, nie mogą one być, że tak powiem, jedną kontynuacją drugiej. Jak już wiadomo, w przypadku, który rozważamy z trzema wymiarami, zgodnie z ogólną teorią, można zbudować tylko trzy trójek liniowo niezależnych wektorów w pewnym układzie współrzędnych (bez względu na rodzaj).

Samolot w przestrzeni trójwymiarowej

Jeśli weźmiemy pod uwagę koncepcję płaszczyzny, bez wchodzenia w definicje matematyczne, dla prostszego zrozumienia tego terminu, taki obiekt można uznać wyłącznie za dwuwymiarowy. Innymi słowy, jest to nieskończona kolekcja punktów, w których jedna ze współrzędnych jest stała (stała).

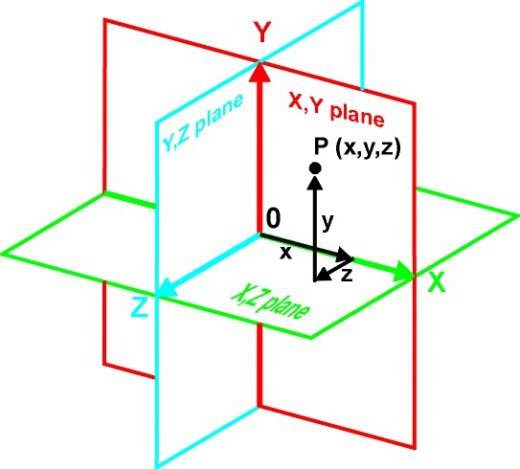
Na przykład płaszczyzna może być nazywana dowolną liczbą punktów o różnych współrzędnych wzdłuż osi X i Y, ale z tymi samymi współrzędnymi wzdłuż osi Z. W każdym przypadku jedna z trójwymiarowych współrzędnych pozostaje niezmieniona. Jest to jednak, by tak rzec, ogólny przypadek. W niektórych sytuacjach przestrzeń trójwymiarowa może przecinać się z płaszczyzną wzdłuż wszystkich osi.

Czy jest więcej niż trzy wymiary

Pytanie, ile pomiarów może istnieć, jest dość interesujące. Uważa się, że nie żyjemy w trójwymiarowym z klasycznego punktu widzenia przestrzeni, ale w czterowymiarowym. Oprócz dobrze znanych długości, szerokości i wysokości, ta przestrzeń obejmuje również czas życia obiektu, a czas i przestrzeń są ze sobą dość mocno powiązane. Zostało to udowodnione przez Einsteina w jego teorii względności, chociaż odnosi się bardziej do fizyki niż do algebry i geometrii.

Kolejnym interesującym faktem jest to, że dzisiaj naukowcy udowodnili już istnienie co najmniej dwunastu wymiarów. Oczywiście, daleko od wszystkich będzie w stanie zrozumieć, czym są, ponieważ odnosi się raczej do pewnego abstrakcyjnego obszaru, który jest poza ludzkim postrzeganiem świata. Niemniej jednak pozostaje faktem. I nie bez powodu wielu antropologów i historyków twierdzi, że nasi przodkowie mogli mieć jakieś specyficzne rozwinięte narządy zmysłów, takie jak trzecie oko, które pomogły w postrzeganiu wielowymiarowej rzeczywistości, a nie tylko trójwymiarowej przestrzeni.

Nawiasem mówiąc, jest dziś sporo opinii na temat tego, że pozazmysłowa percepcja jest również jednym z przejawów postrzegania wielowymiarowego świata i można znaleźć całkiem sporo dowodów.

Należy zauważyć, że współczesne podstawowe równania i twierdzenia opisują wielowymiarowe przestrzenie, które różnią się od naszego czterowymiarowego świata, nie zawsze jest to również możliwe. A nauka w tej dziedzinie odnosi się bardziej do dziedziny teorii i założeń niż do tego, co można wyraźnie odczuć, lub, że tak powiem, dotknąć lub zobaczyć z pierwszej ręki. Niemniej pośredni dowód istnienia wielowymiarowych światów, w których mogą istnieć cztery lub więcej wymiarów, jest dziś ponad wszelką wątpliwość.

Wniosek

Ogólnie rzecz biorąc, bardzo krótko przejrzeliśmy podstawowe pojęcia związane z przestrzenią trójwymiarową i podstawowymi definicjami. Naturalnie istnieje wiele specjalnych przypadków związanych z różnymi układami współrzędnych. Ponadto staraliśmy się nie wchodzić w dziczy matematyki, aby wyjaśnić podstawowe pojęcia, tylko po to, aby pytanie z nimi związane było zrozumiałe dla każdego ucznia (że tak powiem, wyjaśnienie brzmi "na palcach").

Wydaje się jednak, że nawet z tak prostych interpretacji można wywnioskować, że matematyczne aspekty wszystkich elementów zawartych w szkolnym kursie algebry i geometrii.