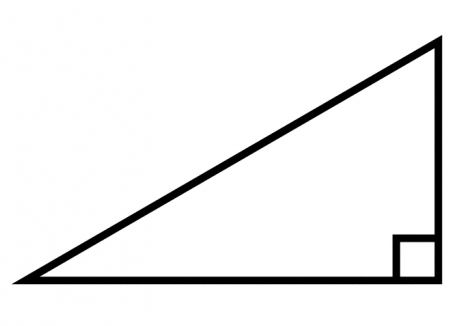
Rodzaje trójkątów. Kąt trójkąta

Najprostszym wielokątem, który studiuje w szkole, jest trójkąt. Jest bardziej zrozumiały dla studentów i napotyka mniej trudności. Pomimo tego, że istnieją różne rodzaje trójkątów, które mają specjalne właściwości.

Jaki kształt nazywa się trójkątem?

Utworzone przez trzy punkty i segmenty. Pierwsze nazywa się wierzchołkami, a drugie - bokami. Co więcej, wszystkie trzy segmenty powinny być połączone, tworząc kąty pomiędzy nimi. Stąd nazwa postaci "trójkąt".

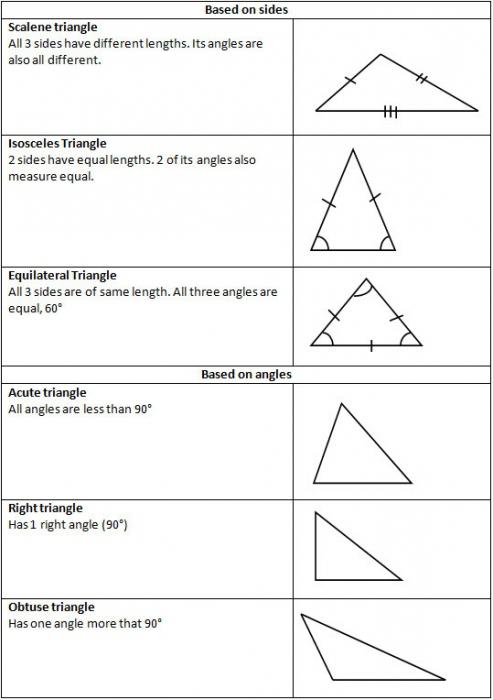
Różnice w nazwach rogów

Ponieważ mogą być ostre, tępe i proste, wtedy typy trójkątów są określane przez te nazwy. W związku z tym istnieją trzy grupy takich liczb.

• Pierwszy. Jeśli wszystkie rogi trójkąta są ostre, wówczas będzie mieć nazwę ostrego kąta. Wszystko jest logiczne.

• Drugi. Jeden z rogów jest rozwarty, co oznacza trójkątny narożnik. Po prostu nie ma miejsca.

• Trzeci. Istnieje kąt 90 stopni, który nazywa się prosto. Trójkąt staje się prostokątny.

Różnice w nazwach po bokach

W zależności od cech boków wyróżniamy następujące typy trójkątów:

• ogólny przypadek jest uniwersalny, w którym wszystkie strony mają dowolną długość;

• równoramienny, którego dwie strony mają te same wartości liczbowe;

• równoboczny, długości wszystkich jego boków są takie same.

Jeśli zadanie nie określa określonego typu trójkąta, musisz narysować dowolny. W którym wszystkie kąty są ostre, a boki mają różne długości.

Właściwości wspólne dla wszystkich trójkątów

1. Jeśli dodasz wszystkie rogi trójkąta, otrzymasz liczbę równą 180º. I bez względu na to, jak wygląda. Ta zasada jest zawsze ważna.
2. Wartość liczbowa dowolnej strony trójkąta jest mniejsza niż pozostałych dwóch dodanych razem. Jednocześnie jest to więcej niż różnica.
3. Każdy zewnętrzny narożnik ma wartość, którą uzyskuje się przez dodanie dwóch wewnętrznych, nie sąsiadujących z nim. Co więcej, zawsze jest czymś więcej niż wewnętrznym przylegającym do niego.
4. Naprzeciwko mniejszej strony trójkąta jest zawsze najmniejszy kąt. I odwrotnie, jeśli strona jest duża, kąt będzie największy.

Te właściwości są zawsze ważne, bez względu na to, jakie trójkąty są uwzględniane w problemach. Wszystkie pozostałe wynikają z określonych funkcji.

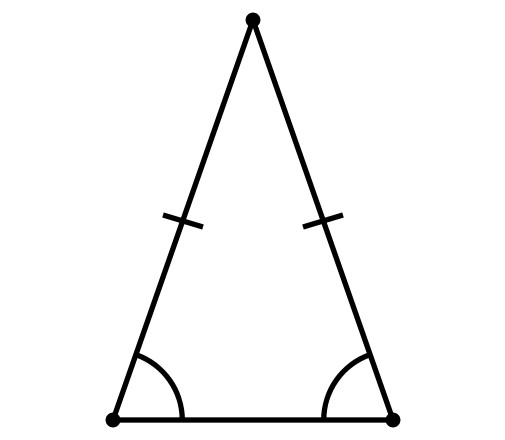
Właściwości trójkąta równoramiennego

• Kąty przylegające do podstawy są równe.
• Wysokość, która jest trzymana do podstawy, jest również medianą i dwusieczną.
• Wysokości, mediany i dwusieczne, które są zbudowane po bokach trójkąta, są odpowiednio sobie równe.

Właściwości trójkąta równobocznego

Jeśli istnieje taka liczba, wszystkie właściwości opisane powyżej będą prawdziwe. Ponieważ równoboczny zawsze będzie równoramienny. Ale nie na odwrót, trójkąt równoramienny niekoniecznie będzie równoboczny.

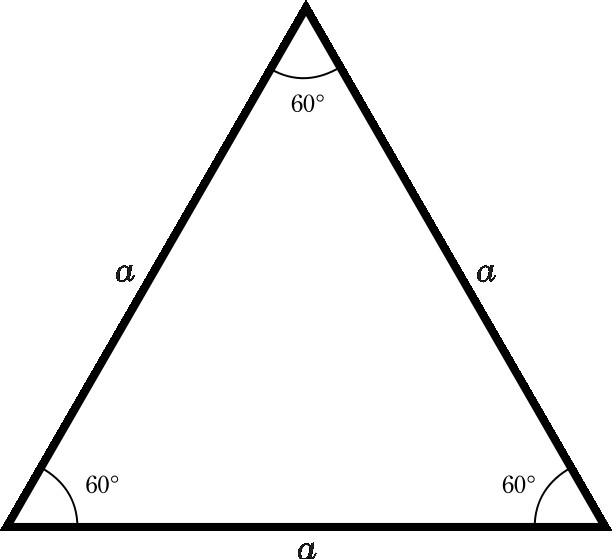
• Wszystkie jego kąty są sobie równe i mają wartość 60º.
• Każda mediana trójkąta równobocznego jest jego wysokością i dwusieczną. I wszyscy są sobie równi. Aby określić ich wartości, istnieje formuła składająca się z produktu strony pierwiastek kwadratowy od 3 podzielone przez 2.

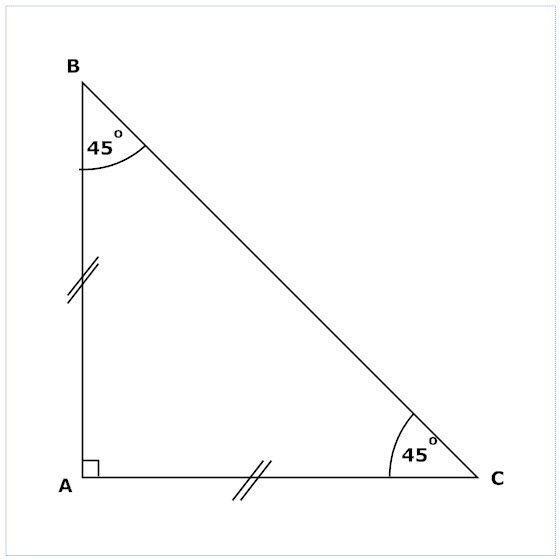
Właściwości trójkąta prostokątnego

• Dwa ostre kąty dają całkowitą wartość 90º.
• Długość przeciwprostokątnej jest zawsze większa niż długość każdej z nóg.
• Wartość liczbowa mediany przeprowadzonej do przeciwprostokątnej stanowi połowę tej wartości.
• Ta sama wartość jest równa długości nogi, jeśli leży ona pod kątem 30 °.
• Wysokość, która jest pobierana od wierzchołka o wartości 90º, ma pewną matematyczną zależność od nóg: 1 / n ² = 1 / a ² + 1 / in ² . Tutaj: a, c - nogi, n - wysokość.

Zadania z różnymi typami trójkątów

№1. Podano trójkąt równoramienny. Jego obwód jest znany i wynosi 90 cm, wymaga znajomości jego boków. Jako dodatkowy warunek: bok jest mniejszy niż podstawa 1,2 razy.

Rozwiązanie

Wartość obwodu jest bezpośrednio zależna od wartości, które należy znaleźć. Suma wszystkich trzech boków da 90 cm Teraz musimy przypomnieć znak trójkąta, w którym jest równoramienny. Oznacza to, że obie strony są równe. Możesz utworzyć równanie z dwoma niewiadomymi: 2a + b = 90. Tutaj a jest bokiem, w - podstawą.

Jest to obrót dodatkowego warunku. Następnie otrzymuje się drugie równanie: в = 1,2а. Możesz zastąpić to wyrażenie w pierwszym. Okazuje się, że: 2a + 1,2a = 90. Po przekształceniach: 3.2a = 90. Stąd a = 28,125 (cm). Teraz łatwo jest znaleźć podstawę. Najlepiej zrobić to z drugiego warunku: c = 1,2 * 28,25 = 33,75 (cm).

Aby to sprawdzić, możesz dodać trzy wartości: 28.125 * 2 + 33,75 = 90 (cm). Zgadza się.

Odpowiedź: boki trójkąta to 28,125 cm, 28,125 cm, 33,75 cm.

№2. Strona trójkąta równobocznego ma 12 cm, konieczne jest obliczenie jego wysokości.

Decyzja. Aby wyszukać odpowiedź, wystarczy powrócić do punktu, w którym opisano właściwości trójkąta. Jest to wzór na znalezienie wysokości, środkowej i dwusiecznej trójkąta równobocznego.

n = a * √3 / 2, gdzie n jest wysokością i a jest bokiem.

Podstawienie i obliczenie daje następujący wynik: n = 6 √3 (cm).

Ta formuła nie musi być pamiętana. Wystarczy przypomnieć, że wysokość dzieli trójkąt na dwa prostokątne. Co więcej, okazuje się, że jest to noga, a przeciwprostokątna jest po stronie oryginału, druga noga jest połową znanej strony. Teraz musisz napisać twierdzenie Pitagorasa i wyprowadzić wzór na wysokość.

Odpowiedź: wysokość to 6 √ 3 cm.

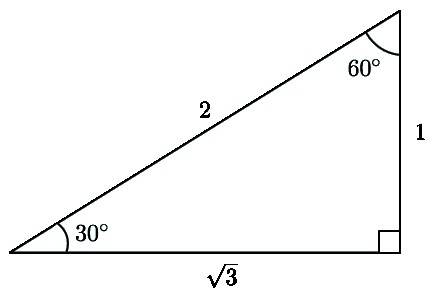
№3. Podaje się MKR - trójkąt, 90 stopni, w którym kąt jest kątowy. Boki MR i KR są znane, mają odpowiednio 30 i 15 cm, konieczne jest poznanie wartości kąta R.

Decyzja. Jeśli wykonasz rysunek, staje się jasne, że MR jest przeciwprostokątną. I to jest dwa razy noga KR. Ponownie musisz odwołać się do właściwości. Jeden z nich połączony jest z narożnikami. Na podstawie tego widać, że kąt CMR jest równy 30º. Zatem pożądany kąt P będzie równy 60º. Wynika to z innej właściwości, która stwierdza, że ​​suma dwóch kątów ostrych powinna wynosić 90 °.

Odpowiedź: kąt P wynosi 60 °.

№4. Musisz znaleźć wszystkie kąty trójkąta równoramiennego. O nim wiadomo, że kąt zewnętrzny od kąta przy podstawie wynosi 110º.

Decyzja. Ponieważ podany jest tylko zewnętrzny narożnik, należy go użyć. Tworzy się wewnętrznie kąt rozwinięty. Łącznie dadzą 180º. Oznacza to, że kąt u podstawy trójkąta będzie równy 70º. Ponieważ jest to równoramienny, drugi kąt ma to samo znaczenie. Pozostaje obliczyć trzeci kąt. Według własności wspólnej dla wszystkich trójkątów suma kątów wynosi 180 °. Stąd trzeci jest zdefiniowany jako 180º - 70º - 70º = 40º.

Odpowiedź: kąty to 70º, 70º, 40º.

№5. Wiadomo, że w trójkącie równoramiennym kąt leżący naprzeciwko podstawy wynosi 90 °. Na podstawie zaznaczonego punktu. Segment łączący go z kątem prostym dzieli go w stosunku 1 do 4. Musisz znać wszystkie kąty mniejszego trójkąta.

Decyzja. Jeden z narożników można natychmiast zidentyfikować. Od trójkąt prostokątny i równoramienne, to te, które leżą u jego podstawy, będą miały 45º, czyli 90º / 2.

Drugi z nich pomoże znaleźć znaną w relacji warunku. Ponieważ jest on równy 1 do 4, wówczas części, na które jest podzielony, otrzymuje tylko 5. Dlatego, aby znaleźć mniejszy kąt trójkąta, potrzebujesz 90º / 5 = 18º. Pozostaje uczyć się trzeciego. Aby to zrobić, od 180º (suma wszystkich kątów trójkąta), odejmij 45º i 18º. Obliczenia są proste i wykażą: 117º.

Odpowiedź: 18º, 45º, 117º