Jaka jest masa elektronu?

Wiadomo, że elektrony mają ładunek ujemny. Ale jak możemy się upewnić, że masa elektronowa i jej ładunek są stałe dla wszystkich tych cząstek? Możesz to sprawdzić, łapiąc w locie. Zatrzymując się, gubi się w cząsteczkach i atomach, które składają się na sprzęt laboratoryjny. Proces poznawania mikrokosmosu i jego cząstek przeszedł długą drogę: od pierwszych prymitywnych eksperymentów do najnowszych osiągnięć w dziedzinie eksperymentalnej fizyki atomowej.

Pierwsza informacja o elektronach

Sto pięćdziesiąt lat temu elektrony nie były znane. Pierwszym dzwonem, wskazującym na istnienie "cegieł" elektryczności, były eksperymenty na elektrolizie. We wszystkich przypadkach każda naładowana cząstka substancji nosiła standardowy ładunek elektryczny o tej samej wielkości. W niektórych przypadkach kwota opłaty podwoiła się lub potroiła, ale zawsze pozostała wielokrotnością jednej minimalnej wartości opłaty.

Eksperymenty J. Thompsona

W laboratorium Cavendisha J. Thomson przeprowadził eksperyment, który faktycznie udowodnił istnienie cząstek elektryczności. Aby to zrobić, naukowiec zbadał promieniowanie emitowane przez lampy katodowe. W eksperymencie promienie odpychały od ujemnie naładowanej płyty i przyciągały ją do naładowanego dodatnio. Stwierdzono hipotezę stałej obecności w polu elektrycznym niektórych cząstek elektrycznych. Ich prędkość była porównywalna z prędkość światła.Ładunek elektryczny pod względem masy cząstek okazało się niewiarygodnie duże. Z jego obserwacji Thompson wyciągnął kilka wniosków, które zostały później potwierdzone przez inne badania.

Wnioski Thompsona

1. Atomy mogą zostać złamane, gdy bombardowane są szybszymi cząsteczkami. W tym przypadku ujemnie naładowane ciałka są wyrzucane ze środka atomów.
2. Wszystkie naładowane cząstki mają taką samą masę i ładunek, niezależnie od substancji, z której zostały otrzymane.
3. Masa tych cząstek jest znacznie mniejsza niż masa najlżejszego atomu.
4. Każda cząsteczka substancji przenosi najmniejszą możliwą frakcję ładunków elektrycznych, z których najmniej nie ma w przyrodzie. Każde naładowane ciało przenosi całą liczbę elektronów.

Szczegółowe eksperymenty pozwoliły obliczyć parametry tajemniczych mikrocząstek. W rezultacie stwierdzono, że otwarte naładowane ciałka są niepodzielnymi atomami elektryczności. Następnie nadano im nazwę elektronów. Pochodził ze starożytnej Grecji i okazał się odpowiedni do opisu nowo odkrytej cząstki.

Bezpośredni pomiar prędkości elektronowej

Ponieważ nie ma możliwości zobaczenia elektronu, eksperymenty niezbędne do pomiaru podstawowych wielkości tej elementarnej cząstki są dokonywane za pomocą pól elektromagnetycznych i grawitacyjnych. Jeśli pierwsza wpływa tylko na ładunek elektronów, to stosując cienkie eksperymenty, biorąc pod uwagę efekt grawitacyjny, można w przybliżeniu obliczyć masę elektronową.

Elektroniczny pistolet

Pierwsze pomiary mas i ładunków elektronów przeprowadzono za pomocą działa elektronowego. Głęboka próżnia w korpusie pistoletu umożliwia przenoszenie elektronów wąską wiązką z jednej katody na drugą. 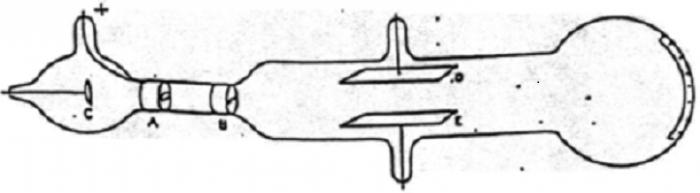Elektrony są zmuszane do przejścia przez wąskie otwory dwa razy ze stałą prędkością v . Istnieje proces podobny do tego, w jaki sposób strumień z węża ogrodowego dostaje się do otworu w ogrodzeniu. Fragmenty elektronów przelatują wzdłuż rury ze stałą prędkością. Udowodniono eksperymentalnie, że jeśli napięcie przyłożone do działa elektronowego wynosi 100 V, wówczas prędkość elektronu będzie obliczana jako 6 milionów m / s.

Wnioski eksperymentalne

Bezpośredni pomiar prędkości elektronowej pokazuje, że niezależnie od materiałów, z których wykonany jest pistolet i jakie są różnice potencjałów, stosunek e / m = const jest spełniony.

Wniosek ten powstał na początku XX wieku. Homogeniczne wiązki naładowanych cząstek nie były jeszcze w stanie stworzyć, do eksperymentów użyto innych urządzeń, ale wynik pozostał taki sam. Eksperyment pozwolił nam wyciągnąć kilka wniosków. Stosunek ładunku elektronu do jego masy jest taki sam dla elektronów. To pozwala wnioskować o uniwersalności elektronu jako integralnej części każdej materii w naszym świecie. Przy bardzo dużych prędkościach e / m jest mniejsze niż oczekiwano. Ten paradoks jest całkiem zrozumiały dzięki temu, że przy dużych prędkościach, porównywalnych do prędkości światła, masa cząstki wzrasta. Warunki brzegowe transformacji Lorentza sugerują, że gdy prędkość ciała jest równa prędkości światła, masa tego ciała staje się nieskończona. Zauważalny wzrost masy elektronowej następuje w pełnej zgodzie z teorią względności.

Elektron i jego masa spoczynkowa

Paradoksalny wniosek, że masa elektronowa nie jest stała, pociąga za sobą kilka interesujących wniosków. W stanie normalnym masa spoczynkowa elektronu się nie zmienia. Można go zmierzyć na podstawie różnych eksperymentów. Obecnie masa elektronowa jest mierzona kilka razy i wynosi 9.10938291 (40) · 10⁻³¹ kg Elektrony o takiej masie wchodzą reakcje chemiczne utworzyć ruch prąd elektryczny uchwycone przez najdokładniejsze instrumenty rejestrujące reakcje jądrowe. Zauważalny wzrost tej wartości jest możliwy tylko przy prędkościach zbliżonych do prędkości światła.

Elektrony w kryształach

Fizyka ciała stałego jest nauką, która obserwuje zachowanie naładowanych cząstek w kryształach. Rezultatem licznych eksperymentów było stworzenie specjalnej ilości charakteryzującej zachowanie elektronu w polach sił substancji krystalicznych. Jest to tak zwana skuteczna masa elektronowa. Jego wartość jest obliczana na podstawie faktu, że ruch elektronu w krysztale podlega dodatkowym siłom, których źródłem jest sam sieć krystaliczna. Taki ruch można opisać jako standard dla swobodnego elektronu, ale przy obliczaniu pędu i energii takiej cząsteczki należy wziąć pod uwagę nie resztę masy elektronu, ale efektywną, której wartość będzie różna.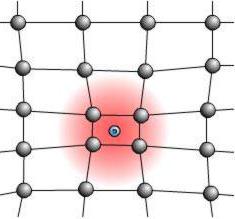

Impuls elektronowy w krysztale

Stan dowolnej cząstki swobodnej można scharakteryzować przez wielkość jej pędu. Ponieważ wartość impulsu została już określona, ​​wówczas, zgodnie z zasadą niepewności, współrzędne cząstek wydają się być rozmyte w całym krysztale. Prawdopodobieństwo spotkania elektronu w dowolnym punkcie sieci krystalicznej jest prawie takie samo. Impuls elektronowy charakteryzuje jego stan w dowolnej współrzędnej pola energii. Obliczenia pokazują, że zależność energii elektronowej od jej pędu jest taka sama jak w przypadku cząstki swobodnej, ale masa elektronowa może przyjąć wartość, która różni się od zwykłej. Ogólnie energia elektronowa, wyrażona poprzez impuls, będzie miała postać E (p) = p ² / 2m *. W tym przypadku m * jest skuteczną masą elektronową. Praktyczne zastosowanie efektywnej masy elektronu jest niezwykle ważne w opracowywaniu i badaniu nowych materiałów półprzewodnikowych stosowanych w elektronice i mikrotechnologii.

Masa elektronu, jak każdy inny kwazicząstek, nie może być scharakteryzowana przez standardowe cechy właściwe dla naszego Wszechświata. Każda cecha mikrocząstki może zaskoczyć i rzucić wyzwanie wszystkim naszym pomysłom na temat otaczającego nas świata.