Postęp algebraiczny: formuły i przykłady rozwiązań
W tym artykule omówimy postęp algebraiczny, formuły niezbędne do rozwiązania problemów z jej udziałem, a także kilka przykładów ich użycia. Dla kompletności krótko mówimy o innym rodzaju postępu - geometrycznym.
Pojęcie progresji algebraicznej

Każda seria liczb uporządkowana według pewnego prawa może być nazywana progresją. Najpopularniejszym i wykorzystywanym do rozwiązywania praktycznych problemów są dwa typy takich serii: progresja algebraiczna i geometryczna. Przyjrzyj się pierwszemu z nich bardziej szczegółowo.
Algebraiczny jest często nazywany postępem arytmetycznym. Matematycznie oznacza to:
a n = a n-1 + d
Oznacza to, że mówimy o takiej kolejności liczbowej, w której każdy z jej członków różni się od poprzedniego lub następnego o tę samą liczbę d. Ta liczba nazywa się różnicą (można ją określić, znajdując różnicę między dwoma sąsiednimi elementami progresji).
Zgodnie z tą definicją rozważany rozwój ma początek, ale nie ma końca. Zawsze zaczyna się od słowa a 1 (dowolna liczba rzeczywista), a następnie przechodzi przez zsumowanie tego członka z różnicą d. Odpowiednio, może on być nieskończenie wzrastający (d> 0) lub malejący (d <0). Sytuacja, w której d = 0 można również uznać za szczególny przypadek postępu arytmetycznego reprezentowanego przez nieskończoną sekwencję identycznych liczb.
Formuła znajdowania dowolnego członka
Jak wyjaśniono powyżej, rodzaj rozpatrywanego postępu jest jednoznacznie określony przez jego pierwszy element i różnicę, ale ta reguła ma zastosowanie do dowolnych innych wartości. Na przykład znajomość dwóch dowolnych elementów lub jednego elementu i suma określonej liczby członków jednoznacznie określa postęp.
Aby obliczyć n-ty element, można z powodzeniem zastosować następującą formułę:
a n = a 1 + (n - 1) * d
Oczywistość ważności tego wyrażenia jest ponad wszelką wątpliwość i każdy może je zweryfikować, zastępując małe wartości n.
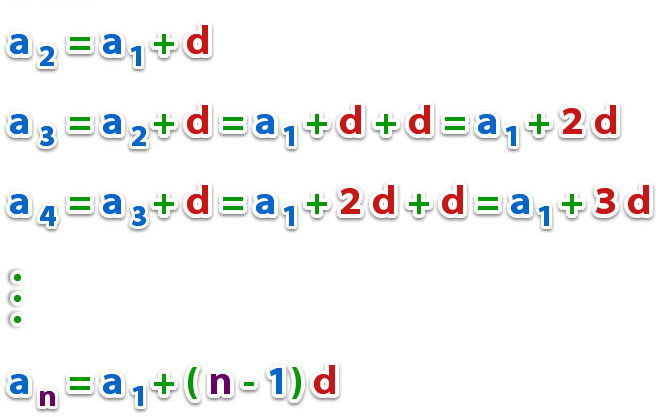
Wzór do przywrócenia postępu dwóch znanych elementów
W szkolnym kursie algebry takie problemy są typowe dla progresji: są dwa elementy a i m , i n> m, konieczne jest zbudowanie na nich całej progresji.
Ten problem został rozwiązany za pomocą wzoru dla n-tego członka. Wypiszemy dwa odpowiadające im wyrażenia:
a n = a 1 + (n - 1) * d;
a m = a 1 + (m - 1) * d
Znajdź różnicę między pierwszym a drugim (znak równości jest zachowany):
a n - a m = (n - m) * d =>
d = (a n - a m ) / (n - m)
Widzimy, jak łatwo jest znaleźć różnicę w progresji, jeśli dwóch jej członków jest znanych: aby to zrobić, należy odjąć mniejszą od większej, a następnie podzielić powstałą różnicę przez różnicę ich numerów sekwencji.
Po znalezieniu różnicy, łatwo jest obliczyć pierwszy termin (w tym celu użyj jednego z dwóch pierwszych wyrażeń).
Suma progresji algebraicznej
Kolejną serią typowych zadań dla rozwoju jest znalezienie sumy swoich członków. Poniżej znajduje się odpowiednia formuła sumy algebraicznej:
S n = Σ i = 1 n (a i ) = n * (a 1 + a n ) / 2
To znaczy, aby określić sumę pierwszych warunków n, należy obliczyć sumę tylko dwóch z nich (pierwsza i n-ta), pomnożyć przez liczbę n i podzielić wynik na połowę.
Pomijamy matematyczny dowód tego wyrażenia, ale wciąż dajemy logiczny dowód. Można zauważyć, że z uwagi na właściwość rozpatrywanego rodzaju progresji zawsze obowiązuje następująca równość:
a 1 + a n = a 2 + a n-1
Rzeczywiście, drugi termin jest większy niż pierwszy termin przez d, ale ten sam przedostatni (a n-1 ) jest mniejszy niż ostatni ( n ). W przypadku pary elementów otrzymujemy dokładnie połowę takich sum z całkowitej liczby elementów (n / 2), z czego wynika zredukowana formuła dla S n .

Uważa się, że zauważona cecha postępu arytmetycznego została po raz pierwszy ustalona przez Karla Gaussa, znanego matematyka z końca XVIII - pierwszej połowy XIX wieku, kiedy w myślach przez kilka sekund obliczył sumę liczb naturalnych od jednego do 100.
Przykłady rozwiązywania problemów
Rozważ dwa przykłady algebraicznej progresji.
1. Wiadomo, że dziewiąty semestr wynosi 7, a 21 jest 51. Konieczne jest znalezienie pierwszych 5 członków tej arytmetycznej progresji.
Stan problemu pozwala nam natychmiast obliczyć różnicę d, stosując formułę z n i m , co zostało opisane powyżej. Mamy:
d = (a n - a m ) / (n - m) = (51 - 7) / (21 - 9) = 3 667
Po otrzymaniu różnicy d, zaokrąglono do 3 miejsc dziesiętnych.
Teraz możesz obliczyć pierwszy element serii. Aby to zrobić, użyj danych dla 9 członków:
a 9 = a 1 + d * 8 => a 1 = a 9 - d * 8 = 7 - 3,667 * 8 = -22,336
Aby rozwiązać problem, należy wykonać ostatni krok: dodawać kolejno 4-krotność wartości d do pierwszego elementu. Otrzymujemy:
a 1 = -2336;
a 2 = -23336 + 3667 = -18,669;
a 3 = -18,669 + 3,677 = -15.002;
a 4 = -1 002 + 3 667 = -11,335;
a 5 = -1 1 335 + 3 667 = -7,668
Przypomnij sobie, że wszystkie wyliczone wartości są ważne do trzeciego miejsca po przecinku.
2. Pracownicy składali przepiłowane pnie drzew w formie piramidy. Wiadomo, że ustanowili tylko 33 kłody, a do końca piramidy brakowało tylko 3 kłód. Konieczne jest określenie, ile rzędów kłód złożyło robotników.
Odpowiedź na to pytanie polega na rozwiązaniu algebraicznego progresu, ale aby przejść do tego problemu, musisz ostrożnie poradzić sobie z tym stanem.
Po pierwsze, ponieważ logi sumują się do piramidy, oznacza to, że w każdym poprzednim wierszu było jeszcze jedno logi, to znaczy d = 1. Po drugie, jeśli wiadomo, że przed ukończeniem piramidy brakowało tylko 3 logów, to pozostały dwa górne rzędy pusty:
a 1 = 1, a 2 = a 1 + d = 2, a 1 + a 2 = 3
Uwzględniamy te trzy logi, dodając je do 33 już złożonych i określając nieznaną liczbę wierszy n, używając formuł dla sumy i n-tego członka:
Sn = n * (a 1 + a n ) / 2; a n = a 1 + d * (n - 1) =>
S n = n * (a 1 + a 1 + d * (n - 1)) / 2 = (2 * a 1 - d) / 2 * n + d * n 2/2
Zastępujemy znane dane do ostatniej równości i rozwiązujemy otrzymane równanie kwadratowe dla n:
36 = 0,5 * n + 0,5 * n 2 lub
n 2 + n - 72 = 0
Discriminant: D = 1 - 4 * 1 * (-72) = 289
Korzenie: n = (-1 ± 17) / 2 = (8; -9)
Odrzucimy natychmiast wartość ujemną, ponieważ jest ona sprzeczna z warunkiem problemu. Tak więc 8 rzędów piramidy będzie zawierać 36 kłód. Ponieważ robotnicy nie uzupełnili dwóch górnych rzędów, oznacza to, że dodali tylko 6 rzędów dzienników.
Kilka słów o postępie geometrycznym
Zasadniczo postęp algebraiczny i geometryczny rozpatrywany jest w ramach jednego tematu, dlatego warto dać wyobrażenie o drugim rodzaju uporządkowanych szeregów liczbowych. Tak więc, geometryczny postęp jest serią liczb, które są zgodne z prawem:
a n = a n-1 * r
Oznacza to, że w przeciwieństwie do arytmetyki, tutaj, aby uzyskać wszystkie elementy, nie wolno dodawać jednej liczby, ale mnożyć przez nią (r nazywana jest mianownikiem).
Z definicji jasno wynika, że postęp geometryczny rośnie (maleje) znacznie szybciej niż w arytmetyce.
Jest on często stosowany w geometrii, na przykład przy obliczaniu obszarów figur za pomocą ich podziału na osobne elementy (metoda dzielenia na pół).