Prędkość kątowa. Prędkość kątowa

Odległość i czas potrzebny do pokonania tej odległości wiąże fizyczną koncepcję - prędkość. A u ludzi z reguły definicja tej wartości nie powoduje problemów. Wszyscy rozumieją, że jazda samochodem z prędkością 100 km / h oznacza przejechanie 100 kilometrów w ciągu godziny.

A co, jeśli ciało się obraca? Na przykład zwykły wentylator domowy wykonuje około dziesięciu obrotów na sekundę. Jednocześnie prędkość rotacji łopatek jest taka, że ​​można je łatwo zatrzymać ręcznie bez szkody dla siebie. Ziemia wokół swojej gwiazdy, Słońce, dokonuje jednej rewolucji w ciągu całego roku, czyli ponad 30 milionów sekund, ale jej prędkość na orbicie okołoziemskiej wynosi około 30 kilometrów w ciągu jednej sekundy!

Jak połączyć zwykłą prędkość z prędkością rotacji, jak wygląda formuła prędkości kątowej?

Pojęcie prędkości kątowej

Pojęcie prędkości kątowej wykorzystywane jest w badaniu praw obrotowych. Dotyczy wszystkich obracających się ciał. Czy jest to obrót jakiejś masy wokół drugiej, jak w przypadku Ziemi i Słońca, czy też obrót samego ciała wokół osi biegunowej (dzienny obrót naszej planety).

Różnica między prędkością kątową a prędkością liniową polega na zapisaniu zmiany kąta, a nie odległości w jednostce czasu. W fizyce prędkość kątowa jest zwykle oznaczana literą alfabetu greckiego "omega" - ω.

Klasyczny wzór prędkości kątowej obrotu jest następujący.

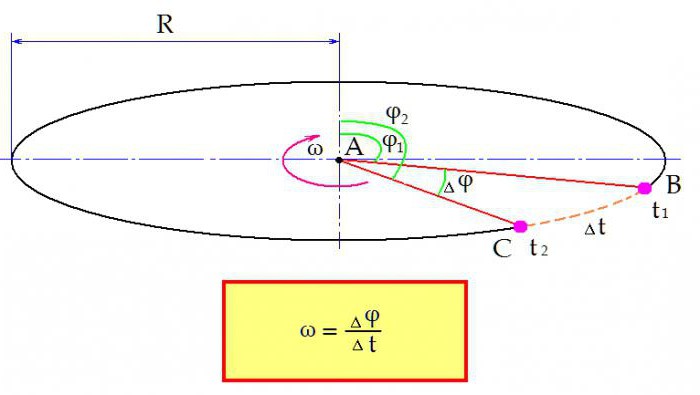
Wyobraź sobie, że ciało fizyczne obraca się wokół pewnego środka A ze stałą prędkością. Jego położenie w przestrzeni względem środka jest określane przez kąt φ. W pewnym momencie czasu t1, rozpatrywany obiekt znajduje się w punkcie B. Kąt odchylenia ciała od początkowego φ1.

Następnie ciało przechodzi do punktu C. Jest tam w czasie t2. Czas potrzebny na ten ruch:

Δt = t2 - t1.

Zmienia się także pozycja ciała w przestrzeni. Teraz kąt odchylenia wynosi φ2. Zmiana kąta w pewnym okresie czasu Δt wynosiła:

Δφ = φ2 - φ1.

Teraz formuła prędkości kątowej jest sformułowana w następujący sposób: prędkość kątowa jest definiowany jako stosunek zmiany kąta Δφ w czasie Δt.

Jednostki prędkości kątowej

Prędkość liniową ciała mierzy się w różnych ilościach. Ruch pojazdów na drogach zwykle wskazuje w kilometrach na godzinę, statki tworzą węzły - mile morskie na godzinę. Jeśli weźmiemy pod uwagę ruch kosmicznych ciał, to najczęściej pojawiają się kilometry na sekundę.

Prędkość kątowa w zależności od wielkości i obracającego się obiektu mierzona jest również w różnych jednostkach.

Radian na sekundę (rad / s) jest klasyczną miarą prędkości w międzynarodowym systemie jednostek (SI). Pokazują, jak radian (w jednym pełnym ruchu 2 2 3,14 radian) ciało ma czas, aby skręcić w jedną sekundę.

Obroty na minutę (rpm) to najczęściej stosowana jednostka do wyznaczania prędkości obrotowych w inżynierii. Wały silników, zarówno elektrycznych, jak i samochodowych, dają dokładnie (po prostu patrzeć na obrotomierz w samochodzie) obroty na minutę.

Obroty na sekundę (rev / s) - używane rzadziej, głównie w celach edukacyjnych.

Okres leczenia

Czasami w celu określenia prędkości obrotowej wygodniej jest zastosować inną koncepcję. Okres krążenia nazywany jest czasem, w którym określony organizm wykonuje obrót o 360 ° (pełne koło) wokół środka obrotu. Formuła prędkości kątowej wyrażona w okresie rewolucji przyjmuje postać:

ω = 2P / T.

Wyrażanie prędkości obrotowej ciał w okresie obiegu jest uzasadnione w przypadkach, gdy ciało obraca się stosunkowo wolno. Powróćmy do rozważań nad ruchem naszej planety wokół gwiazdy.

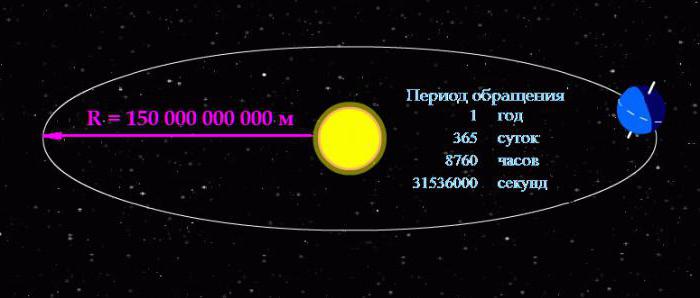
Formuła prędkości kątowej pozwala nam ją obliczyć, znając okres rewolucji:

ω = 2P / 31536000 = 0,000000199238499086111 rad / s.

Patrząc na uzyskany wynik, można zrozumieć, dlaczego, biorąc pod uwagę rotację ciał niebieskich wygodniej jest używać okresu obiegu. Osoba widzi wyraźne liczby przed sobą i wyraźnie wizualizuje ich skalę.

Narożne i liniowe sprzężenie prędkości

W niektórych zadaniach należy zdefiniować prędkość liniową i kątową. Formuła transformacji jest prosta: prędkość liniowa ciała jest równa iloczynowi prędkości kątowej i promienia obrotu. Jak pokazano na rysunku.

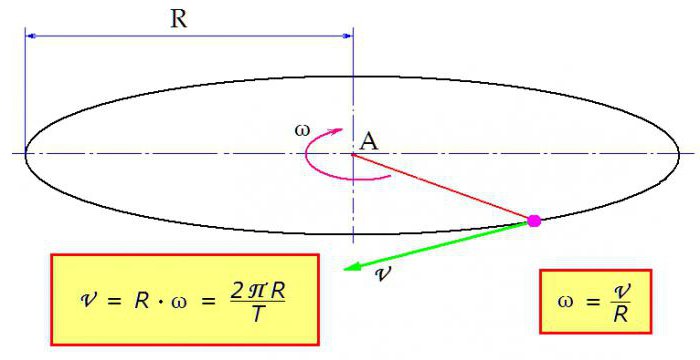
Wyrażenie "działa" w odwrotnej kolejności, z jego pomocą również określana jest prędkość kątowa. Formułę na podstawie prędkości liniowej uzyskuje się za pomocą prostych operacji arytmetycznych.