Moc Archimedesa: przyczyna, wzór i zastosowanie w inżynierii i przyrodzie
Wielu obserwowało statki płynące po morzu, balony latające w atmosferze. Jednak niewiele osób wie, jaki rodzaj siły powoduje wzrost ilości ciał stałych w wodzie i powietrzu. W tym artykule zastanowimy się nad tym, czym jest siła Archimedesa, na czym polega fizyczna przyczyna jej występowania, i jaką formułę stosuje się do obliczenia jej wielkości.
Ciśnienie w objętości płynnej substancji
Aby zrozumieć przyczynę pojawienia się siły Archimedesa, należy wziąć pod uwagę specyfikę istnienia ciśnienia wewnątrz substancji płynących. Takimi substancjami są gazy i ciecze, ponieważ jakakolwiek minimalna siła ścinająca przyłożona do nich prowadzi do przesunięcia w nich pewnych warstw w stosunku do innych, to znaczy, pojawia się przepływ.
Weźmy na przykład płyn (woda, alkohol, benzyna itp.). Po pierwsze, płyn jest nieściśliwy. Po drugie, wszystkie elementarne cząstki, które go tworzą, poruszają się losowo w różnych kierunkach. Ten ruch prowadzi do tego, że każda objętość wewnątrz cieczy jest pod wpływem ciśnienia ze wszystkich stron. Ponieważ każdy element ciśnieniowy odpowiada podobnemu, który jest skierowany w przeciwnym kierunku, całkowite ciśnienie na danej objętości wynosi zero.
Jeśli płyn znajduje się w polu sił grawitacyjnych (na przykład w polu ziemskim), górne warstwy zaczynają naciskać na niższe warstwy. Ciśnienie, które wywierają, nazywa się hydrostatycznym. Określa się to za pomocą następującego wzoru:
P = ρ * g * h.
Gdzie ρ jest gęstością płynu, h jest odległością od powierzchni płynu, czyli głębokości.
Z powodu ciśnienia hydrostatycznego pojawia się siła Archimedesa. Rozważ bardziej szczegółowo w następnym akapicie przyczynę jego pojawienia się.
Siła Archimedesa i Archimedesa
Tradycyjnie uważa się, że odkrycie pływalności i prawa matematycznego, które ją definiuje, należy do Archimedesa. Według legendy użył tego prawa do zdefiniowania fałszywej złotej korony. Prawo Archimedesa można sformułować w następujący sposób: ciało zanurzone w płynnej substancji podlega działaniu siły skierowanej ku górze, która jest równa masie wypartego płynu. Odpychająca siła w fizyce otrzymała nazwę Archimedesa.
Jak już wspomniano, przyczyną siły wyporu jest ciśnienie hydrostatyczne. Faktem jest, że na każdym zanurzonym ciele nacisk wywierany przez ciecz na górną część ciała będzie zawsze mniejszy niż nacisk wywierany na jego dolną część. Różnica między nimi, pomnożona przez obszar oddziaływania, jest siłą popychającą.
Wzór na moc Archimedesa jest zapisany w następujący sposób:
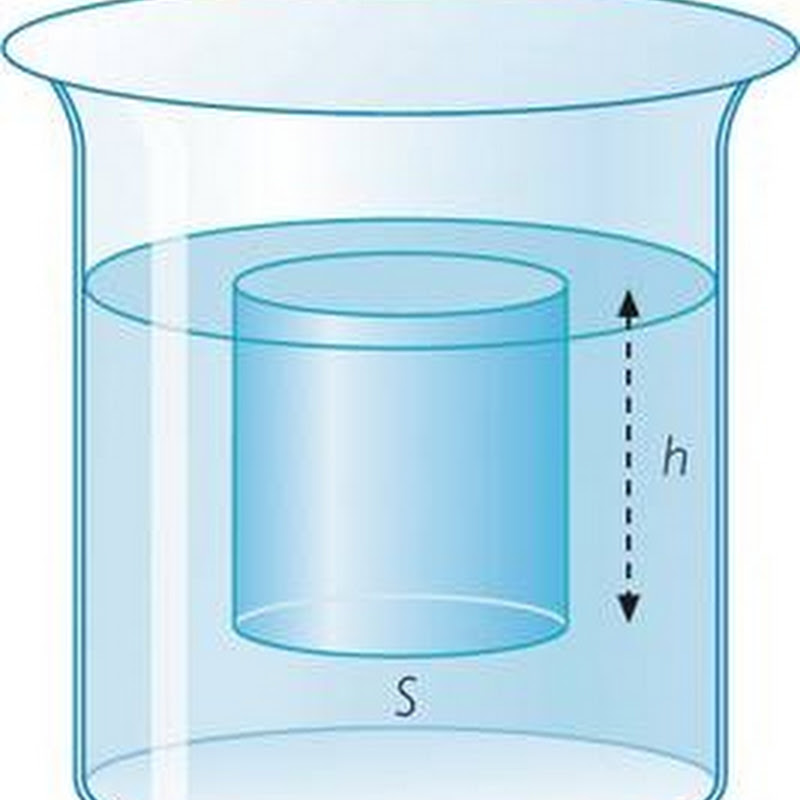
F A = ρ l * g * V l .
Gdzie ρ1 i V1 są gęstością płynu i jego objętością, która została przesunięta przez zanurzony korpus. Nie mylić wartości V l z objętością ciała, która będzie oznaczona jako dalsze Vs. Ponieważ płyn jest nieściśliwy, objętości te będą równe sobie nawzajem tylko przy pełnym zanurzeniu ciała.
Stan pływnych substancji stałych w płynach

To, czy ciało zatopi się w płynie, czy też się w nim unosi, zależy od związku między dwiema siłami (grawitacja i siła Archimedesa). Ponieważ pierwsza jest równa masie ciała, możemy zapisać następującą równość:
m s * g = ρ l * g * V l .
Pisząc masę przez gęstość i przyjmując, że ciało jest całkowicie zanurzone w cieczy, dochodzimy do następującego równania:
ρ s * g * V s = ρ l * g * V l =>
ρ s = ρ l .
Wynikające z tego wyrażenie matematyczne jest warunkiem, że ciało nie unosi się ani nie tonie w płynie. Zawsze będzie na powierzchni płynnej substancji, jeśli jej gęstość jest mniejsza niż gęstość cieczy. Przy odwrotnej zależności pomiędzy tymi gęstościami, ciało zatonie.
Następnie pokażemy, gdzie stosowane jest rozważane prawo i rozwiązujemy problem z jego użyciem.
Pływanie różnymi przedmiotami
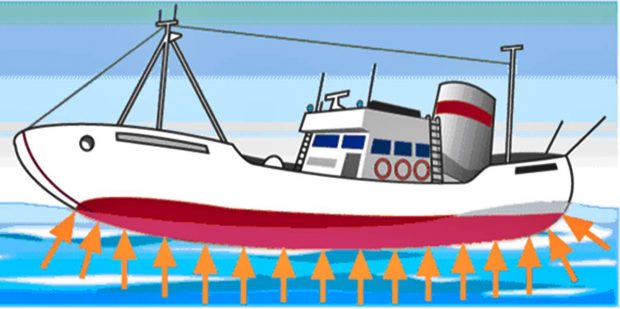
Być może najbardziej znanym przykładem jest żeglarstwo statków. Tak więc, każdy statek ma średnią gęstość mniejszą niż gęstość wody (1 g / cm 3 ), więc nie tonie, mimo że jest zrobiony z dużo gęstszych metalicznych materiałów.
W przypadku łodzi podwodnej należy zauważyć, że jej wyporność jest regulowana za pomocą statecznika. Tak więc, zbierając wodę morską w specjalnie przygotowanych zbiornikach, łódź zwiększa jej średnią gęstość i zaczyna opadać. Przeciwnie, pompowanie wody z tych zbiorników zmniejsza jej średnią gęstość, która prowadzi do wznoszenia się okrętu podwodnego. Zgodnie z tą samą zasadą, ryby z pęcherzem pływackim mogą z łatwością zmienić głębokość nurkowania.
Zasada balonów balonów i balonów nie różni się od pływających statków w wodzie. Na przykład balon używa gorącego powietrza podczas lotu. Jak wiadomo z fizyki, po ogrzaniu gęstość powietrza zmniejsza się z powodu jego rozszerzania. W rezultacie balon ma możliwość podniesienia ładunku w powietrzu przy użyciu siły wyporu.
Przyrząd do pomiaru gęstości
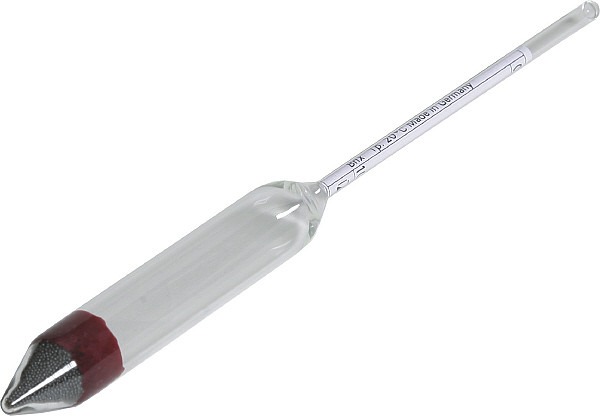
Biorąc pod uwagę prawo Archimedesa i jego zastosowanie, należy stwierdzić, że oprócz żeglugi statków znajduje on zastosowanie przy określaniu gęstości analizowanego płynu. Aby to zrobić, użyj miernika gęstości lub gęstościomierza. Jest to szklana rurka, której dno jest prowadzone. Rurka ma skalę podziałów. Umieszczając urządzenie w jakimkolwiek płynie, dokładnie pokazuje jego gęstość.
Miernik gęstości służy do określenia ładunku baterii, do analizy czystości mleka lub zawartości alkoholu w winie.
Zadanie stosowania prawa Archimedesa
Załóżmy, że balon ma pojemność 1000 m 3 . Gęstość powietrza otaczającego balon wynosi 1,225 kg / m 3 . Konieczne jest określenie, która waga może podnieść piłkę, jeśli gęstość gorącego powietrza w jego objętości wynosi 1 kg / m 3 .

Piszemy wyrażenie równości sił:
P g + P s = F A.
Gdzie P g jest ciężarem ładunku, który unosi piłkę, P s jest wagą samej piłki. Zakładamy, że średnia gęstość kuli jest równa gęstości gorącego powietrza w niej, następnie powyższe wyrażenie może być przepisane jako:
m g * g = V * g * (ρ a - ρ s ).
Gdzie V jest objętością kuli, ρ s jest jej gęstością, ρ a jest gęstością powietrza, m g jest masą uniesionego ładunku. Wtedy m g będzie równe:
m g = V * (ρ a - ρ s ) = 1000 * (1225-1) = 225 kg.
Tak więc ta kula będzie w stanie podnieść 3 osoby o wadze 70 kg każda.