Złożone liczby i akcje na nich

Liczby zespolone w tradycyjnym tego słowa znaczeniu nie są liczbami używanymi do liczenia i mierzenia, ale są obiektami matematycznymi określonymi przez właściwości przedstawione poniżej.

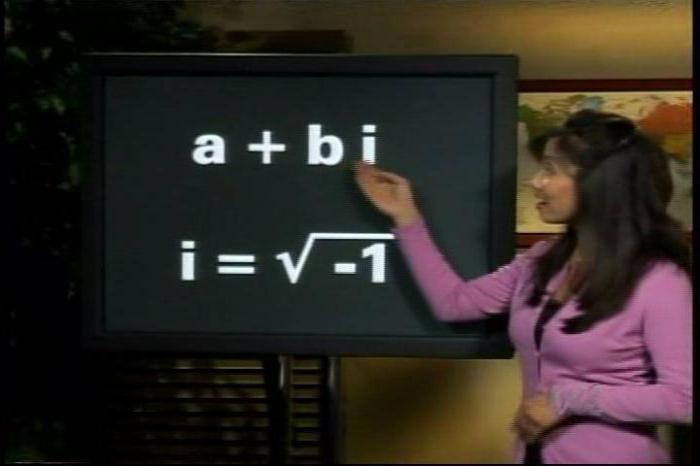
Użyj 3 form liczby zespolonej: algebraicznej, wykładniczej, trygonometrycznej.

Forma algebraiczna

Liczby zespolone są oznaczone przez wyrażenie ω + νi, gdzie ω i ν są rzeczywiste, a symbol i , jest określony przez warunek i ² - 1 - jednostka jest wyimaginowana.

W związku z tym liczba zespolona ω + νi jest podzielona na części rzeczywiste i urojone. Dla wygody jest przedstawiony w postaci jednej litery (na przykład η ): η = ω + νi .

Części liczby zespolonej η = ω + νi , rzeczywiste i urojone, oznaczane są odpowiednio przez ω = Reη, ν = Itη .

Liczby zespolone są uważane za równe, gdy ich części rzeczywiste i urojone są równoważne. Liczba zespolona jest uważana za równą zeru, jeśli jej części, rzeczywiste i urojone, są równe zeru.

Operacje arytmetyczne

Dodawanie

Suma liczb zespolonych jest liczbą zespoloną, której rzeczywista część jest równa sumie rzeczywistych części, a wyimaginowana odpowiada sumie wyimaginowanych części:

η = (ω ₁ + ω ₂ ) + (ν ₁ + ν ₂ ) i.

Mówi się, że wśród złożonych η zyskaliśmy w wyniku dodania liczb kompleksu :

η = η ₁ + η _2.

Złożone η ₁ i η _{2 są} określane jako terminy.

Prawa operacji dodawania:

1) prawo stowarzyszeniowe;

2) prawo komutatywności .

Liczba złożona -ω-bi nazywana jest przeciwną liczbą zespoloną ω + νi . Suma przeciwnych liczb zespolonych wynosi zero.

Różnica

Różnica między liczbami zespolonymi nazywana jest liczbą zespoloną η równą sumie liczby η ₁ i liczby przeciwnej η ₂ :

η = η ₁ + (- η ₂ ) = (ω ₁ -ω ₂ ) + (ν ₁ -ν ₂ ) i.

Liczbę złożonych η przypisuje się odejmując η ₂ i η ₁ (liczby zespolone) i zapisuje:

η = η ₂ -η ₁ .

Praca

Iloczyn liczb zespolonych jest liczbą zespoloną:

η = (ω ₁ ω ₂ -v ₁ ν ₂ ) + (ω ₁ ν ₁ + ω ₂ ν ₁ ) i.

Mówi się, że liczba złożonych η została uzyskana przez pomnożenie η ₁ przez η ₂ (liczby η ₁ i η ₂ są złożone) i zapisują:

η = η ₁ η ₂ .

Złożone η ₁ i η _{2 są} nazywane mnożnikami.

Prawa mnożenia liczb zespolonych:

1) prawo asocjacji ;

2) prawo komutatywności .

Podział

Poszczególne liczby zespolone są nazywane złożonymi η tak, że η ₁ = η _1: η ₂ ( η2 0 ) . Prywatne liczby zespolone są obliczane według wzoru:

η = (ω ₁ ω ₂ -v ₁ ν ₂ ) / (ω ² + ν ² ) + (ω ₁ ν ₁ + ω ₂ ν ₁ ) i / (ω ² + ν ² ).

Liczbę η mówi się, że uzyskano ją przez podzielenie η ₁ przez η ₂ , i zapisano:

η = η ₁ / η _{2 .}

Dodawanie i mnożenie liczb zespolonych jest powiązane z regułą zwaną prawem mnożenia dystrybucji w odniesieniu do dodawania .

Numery zespolone trygonometryczne

Użyj również innej formy rejestrowania liczb zespolonych, która nazywa się trygonometrycznym.

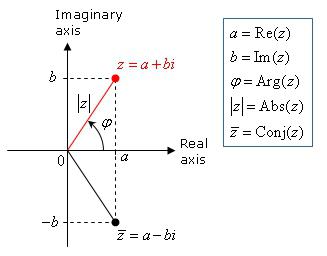
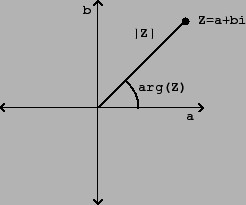
Liczba zespolona ω + νi może być zapisana jako:

η = k (cosβ + isinβ), gdzie k ² = ω ² + ν ² .

Wyrażenie to jest formą rejestrowania liczb zespolonych, która jest nazywana trygonometryczną. Moduł liczby zespolonej jest liczbą rzeczywistą k , a jego argumentem jest kąt β mierzony w radianach.

Jeśli liczba zespolona nie wynosi zero, to jej moduł jest dodatni; jeśli η = 0 , innymi słowy, ω = ν = 0 , to jego moduł jest równy zeru. Moduł jest zdefiniowany w sposób unikalny.

Iloczyn liczby trygonometrycznych liczb zespolonych jest modułem liczby zespolonej, która jest odpowiednikiem iloczynu czynników, a raczej ich modułów, a argument jest równoważny sumie argumentów czynników:

η ₁ η ₂ = k ₁ k ₂ [cos (β ₁ + β ₂ ) + isin (β ₁ + β ₂ )].

Prywatne trygonometryczne liczby zespolone, które nie są zerami, są liczbami zespolonymi, których moduł jest równoważny częściowej dywidendy i dzielnikowi (ich modułów), a argument jest równoważny różnicy argumentów dywidendy i dywizora:

η ₁ / η ₂ = k ₁ / k ₂ [cos (β ₁ -β ₂ ) + isin (β ₁ -β ₂ )].

Naturalny stopień liczby złożonych

W matematyce n-tą potęgą złożonego η jest kompleks znaleziony w wyniku namnażania η kompleksu n razy sam: w = ηη ... η .

Zwykle używaj krótszego wpisu:

w = η ⁿ ,

w którym liczba η jest podstawą stopnia, a n (liczba naturalna) jest wykładnikiem.

N-ta moc η (liczba zespolona), podana w formie trygonometrycznej, jest obliczana według wzoru:

η ⁿ = k ⁿ (cosnβ + isinnβ).

Ta formuła nazywana jest formułą Moivre.