Mianownik progresji geometrycznej: formuły i własności

Progresja geometryczna wraz z arytmetyką jest ważną serią liczbową, która jest studiowana na kursie algebry w klasie dziewiątej. W tym artykule rozważamy mianownik postępu geometrycznego i jak jego wartość wpływa na jego właściwości.

Definicja postępu geometrycznego

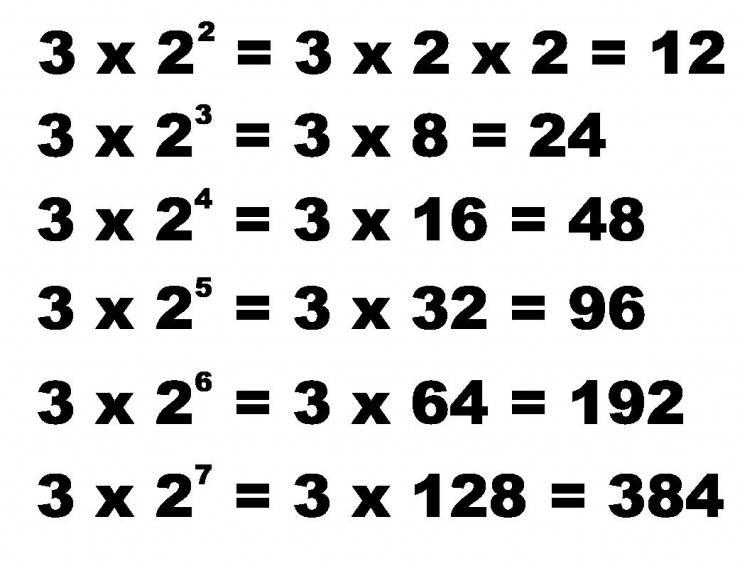
Na początek podajemy definicję tej serii liczb. Progresja geometryczna jest szeregiem liczb wymiernych, tworzonych przez sukcesywne pomnożenie pierwszego elementu przez stałą liczbę, zwaną mianownikiem.

Na przykład liczby w rzędzie 3, 6, 12, 24, ... są postępem geometrycznym, ponieważ jeśli pomnożymy 3 (pierwszy element) przez 2, otrzymamy 6. Jeśli 6 zostanie pomnożone przez 2, otrzymamy 12 i tak dalej.

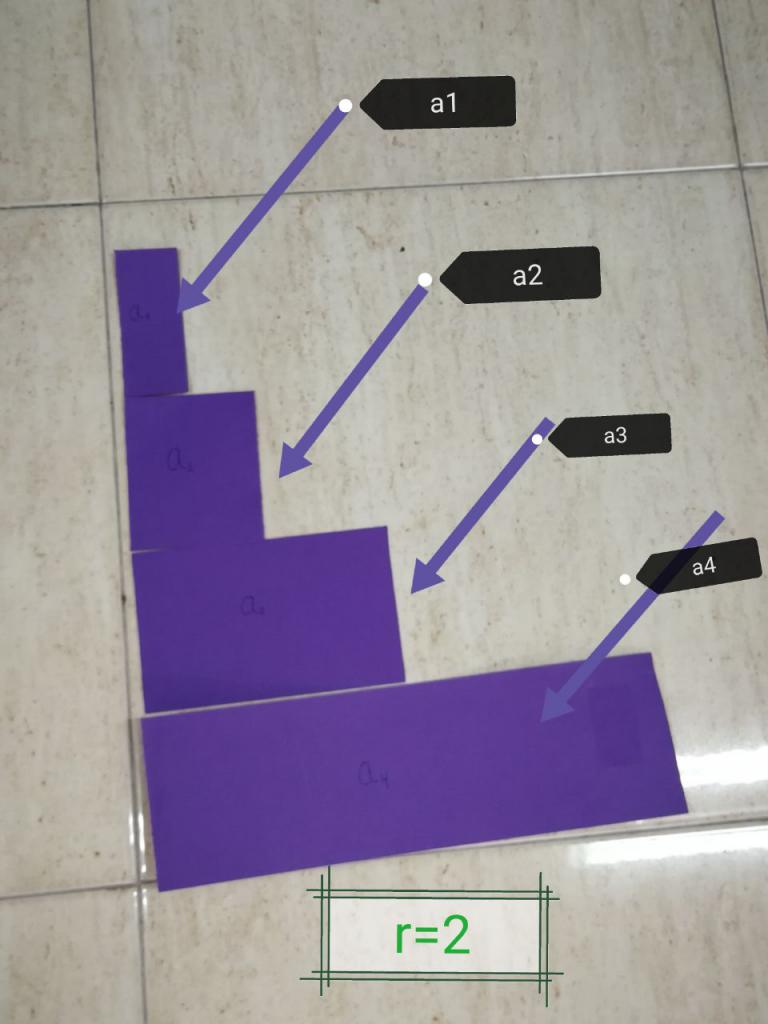
Elementy rozpatrywanej sekwencji są zwykle oznaczone symbolem a, gdzie i jest liczbą całkowitą wskazującą numer elementu w serii.

Powyższą definicję progresji można zapisać w języku matematyki w następujący sposób: a _n = bn ^-1 * a ₁ , gdzie b jest mianownikiem. Łatwo jest sprawdzić tę formułę: jeśli n = 1, to b ^1-1 = 1, a otrzymamy ₁ = a _1. Jeśli n = 2, to a _n = b * a ₁ , i ponownie dochodzimy do definicji rozważanej serii liczb . Podobne argumenty można kontynuować dla dużych wartości n.

Mianownik postępu geometrycznego

Liczba b w pełni określa naturę całej serii liczb. Mianownik b może być dodatni, ujemny, a także mieć wartość większą niż jeden lub mniej. Wszystkie te opcje prowadzą do różnych sekwencji:

• b> 1. Istnieje rosnąca liczba liczb wymiernych. Na przykład 1, 2, 4, 8, ... Jeśli element a ₁ ma wartość ujemną, wówczas cała sekwencja wzrośnie tylko w wartości bezwzględnej, ale zmniejszy się względem znaku liczb.
• b <-1. W tym przypadku mówimy o szeregu zmiennym, to znaczy sąsiednie elementy różnią się znakiem. Na przykład 1, -2, 4, -8, 16, ...
• -1 <b <1. Jest to szczególny przypadek, który ma swoją własną nazwę - malejącą nieskończoną geometryczną progresję. Jego główną cechą jest to, że niezależnie od znaku mianownika ma on skłonność do skończonej sumy przy dodawaniu nieskończonej liczby jej elementów.
• b = 1. Często taki przypadek nie jest nazywany progresją, ponieważ istnieje zwykła seria identycznych liczb wymiernych. Na przykład -4, -4, -4.

Wzór na sumę

Przed przystąpieniem do rozpatrywania konkretnych zadań przy użyciu mianownika danego typu progresji należy podać ważną formułę sumy pierwszych n elementów. Formuła ma postać: S _n = (b ⁿ - 1) * a ₁ / (b - 1).

Możesz uzyskać to wyrażenie, jeśli weźmiesz pod uwagę rekursywną sekwencję członków progresji. Należy również zauważyć, że w powyższym wzorze wystarczy znać tylko pierwszy element i mianownik, aby znaleźć sumę dowolnej liczby członków.

Nieskończenie malejąca sekwencja

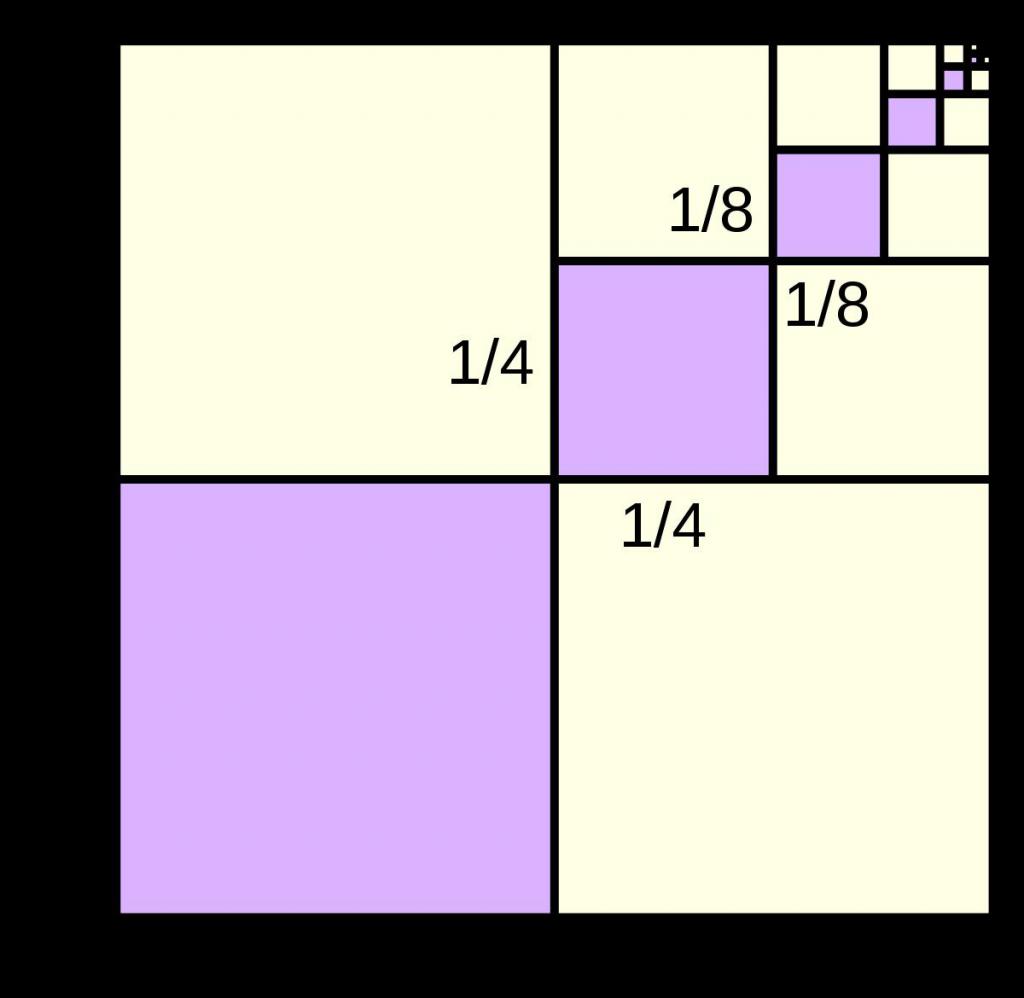
Powyżej podano wyjaśnienie, co to jest. Teraz, znając formułę S _n , zastosuj ją do tej serii liczb. Ponieważ jakakolwiek liczba, której moduł nie przekracza 1, ma tendencję do zera podczas wznoszenia do dużych stopni, to znaczy b ^∞ => 0, jeśli -1 <b <1 (| b | <1), wówczas ogólny wzór dla sumy jest zamieniany na następujące wyrażenie: S _∞ = a ₁ / (1 - b).

Ponieważ różnica (1 - b) zawsze będzie dodatnia, niezależnie od wartości mianownika, znak sumy malejącej nieskończonej progresji geometrycznej S _{∞ jest} jednoznacznie określony przez znak jej pierwszego elementu a ₁ .

Teraz rozważymy kilka zadań, w których pokażemy, jak zastosować zdobytą wiedzę na temat konkretnych liczb.

Numer problemu 1. Obliczanie nieznanych elementów progresji i ilości

Biorąc pod uwagę postęp geometryczny, mianownik progresji 2 i jej pierwszy element 3. Jaka będzie jego siódma i dziesiąta liczba członków, a jaka jest suma jego siedmiu elementów początkowych?

Stan problemu jest dość prosty i wymaga bezpośredniego użycia powyższych formuł. Tak więc, aby obliczyć element z liczbą n, używamy wyrażenia a = bn ^-1 * a ₁ . Dla 7. elementu mamy: a ₇ = b ⁶ * a _1, zastępując znane dane, otrzymujemy: a ₇ = 2 ⁶ * 3 = 192. Postępujemy w ten sam sposób dla 10 elementu: a ₁₀ = 2 ⁹ * 3 = 1536 .

Używamy znanej formuły dla sumy i ustalamy tę wartość dla pierwszych 7 elementów z serii. Mamy: S ₇ = (2 ⁷ - 1) * 3 / (2 - 1) = 381.

Numer problemu 2. Określenie sumy dowolnych elementów progresji

Niech -2 będzie równe mianownikowi progresji w postępie geometrycznym b ^n-1 * 4, gdzie n jest liczbą całkowitą. Konieczne jest określenie ilości od piątego do dziesiątego elementu tej serii włącznie.

Zadany problem nie może być rozwiązany bezpośrednio przy użyciu znanych formuł. Można go rozwiązać za pomocą 2 różnych metod. Dla kompletności podamy oba.

Metoda 1. Jego idea jest prosta: konieczne jest obliczenie dwóch odpowiednich ilości pierwszych elementów, a następnie odjęcie od siebie. Obliczamy mniejszą sumę: S ₁₀ = ((-2) ¹⁰ - 1) * 4 / (-2 - 1) = -1364. Teraz obliczamy dużą ilość: S ₄ = ((-2) ⁴ - 1) * 4 / (-2 - 1) = -20. Zauważ, że w ostatnim wyrażeniu podsumowano tylko 4 terminy, ponieważ piąta jest już uwzględniona w sumie, która ma być obliczona przez warunek problemu. Wreszcie, weź różnicę: S ₅ ¹⁰ = S ₁₀ - S ₄ = -1364 - (-20) = -1344.

Metoda 2. Zanim zastąpisz liczby i policzysz, możesz uzyskać wzór na sumę między członami mi serii badanej serii. Postępujemy w dokładnie taki sam sposób jak w metodzie 1, pracując tylko najpierw z symboliczną reprezentacją sumy. Mamy: S ⁿ _m = (b ⁿ - 1) * a ₁ / (b - 1) - (b ^m-1 - 1) * a ₁ / (b - 1) = a ₁ * (b ⁿ - b ^{m - 1} ) / (b - 1). Możesz zastąpić znane liczby w wynikowym wyrażeniu i obliczyć wynik końcowy: S ¹⁰ ₅ = 4 * ((-2) ¹⁰ - (-2) ⁴ ) / (-2 - 1) = -1344.

Numer problemu 3. Czym jest mianownik?

Niech ₁ = 2, znajdź mianownik postępu geometrycznego, pod warunkiem, że jego nieskończona suma wynosi 3, a wiadomo, że jest to malejąca seria liczb.

Pod warunkiem problemu nie jest trudno odgadnąć, którą formułę należy zastosować w celu rozwiązania problemu. Oczywiście, suma progresji jest nieskończenie malejąca. Mamy: S _∞ = a ₁ / (1 - b). Skąd mamy wyraz mianownik: b = 1 - a ₁ / S _∞ . Pozostaje zastąpić znane wartości i uzyskać wymaganą liczbę: b = 1 - 2/3 = -1 / 3 lub -0.333 (3). Wynik ten można sprawdzić jakościowo, jeśli przypomnimy sobie, że dla tego typu sekwencji moduł b nie może wykraczać poza 1. Jak widać, | -1 / 3 | <1.

Numer problemu 4. Odzyskiwanie szeregu liczb

Niech podane zostaną 2 elementy szeregu liczbowego, np. 5 to 30, a 10 60. Konieczne jest zrekonstruowanie całej serii z tych danych, wiedząc, że spełnia ona cechy geometrycznej progresji.

Aby rozwiązać problem, należy zacząć pisać odpowiednie wyrażenie dla każdego znanego członka. Mamy: a ₅ = b ⁴ * a ₁ i ₁₀ = b ⁹ * a ₁ . Teraz dzielimy drugie wyrażenie na pierwsze, otrzymujemy: a ₁₀ / a ₅ = b ⁹ * a ₁ / (b ⁴ * a ₁ ) = b ⁵ . Stąd wyznaczamy mianownik, przyjmując pierwiastek piątego stopnia ze stosunku znanych terminów z warunku problemu, b = 1,148698. Wynikowa liczba jest podstawiana do jednego z wyrażeń dla znanego elementu, otrzymujemy: a ₁ = a ₅ / b ⁴ = 30 / (1148698) ⁴ = 17,2304966.

W ten sposób ustaliliśmy, czym jest mianownik progresji bn, a przebieg geometryczny b ^n-1 * 17,2304966 = a _n , gdzie b = 1,148698.

Gdzie stosuje się postęp geometryczny?

Gdyby w praktyce nie było zastosowania tej serii liczbowej, jej badania zostałyby zredukowane do czysto teoretycznego zainteresowania. Ale taka aplikacja istnieje.

Oto 3 najbardziej znane przykłady:

• Paradoks Zenona, w którym zręczny Achilles nie może dogonić powolnego żółwia, rozwiązuje się, stosując pojęcie malejącej nieskończonej sekwencji liczb.
• Jeśli umieścisz ziarna pszenicy na każdej komórce szachownicy, połóż 1 ziarno na 1 komórce, 2 na 2, 2 na 3, i tak dalej, to potrzebujesz 18446744073709551615 ziarna, aby wypełnić wszystkie komórki planszy!
• W grze "Wieża Hanoi", aby zmienić układ dysków z jednego pręta na drugi, konieczne jest wykonanie operacji 2 ⁿ - 1, to znaczy ich liczba rośnie wykładniczo wraz z liczbą używanych dysków n.