Wyznaczanie momentu pędu, siły i bezwładności. Równanie chwilowe Przykład rozwiązania problemu

Dynamika rotacji jest jedną z ważnych części współczesnej mechaniki, która uwzględnia prawa ruchu obrotowego ciał wokół osi i punktów. W tym artykule zajmiemy się szczegółowo głównym równaniem dynamiki rotacji - równania momentów.

Moment impulsu

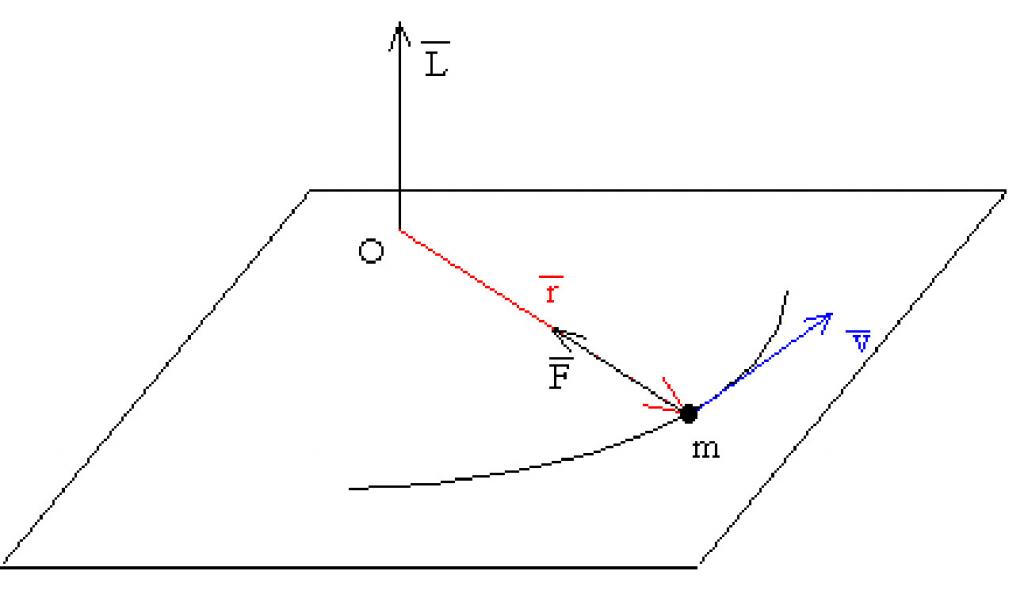
Każdy uczeń wie, co stanowi impuls mechaniczny, który jest bardziej poprawnie nazywany ilością ruchu. Załóżmy teraz, że punkt materialny o masie m obraca się wokół osi O przy prędkości liniowej v. Jeśli promień obrotu jest oznaczony jako r, możemy zapisać następujące wyrażenie:

L¯ = [m * v¯ * r¯].

Dwa pierwsze czynniki po prawej stronie równości to liniowy pęd punktu. Iloczyn tego impulsu przez wektor r¯, skierowany od osi obrotu do punktu, nazywany jest momentem pędu L¯.

Wartość L¯ jest wektorem. Jest skierowany prostopadle do płaszczyzny obrotu punktu. Kierunek momentu pędu punktu materialnego określany jest za pomocą reguły prawej ręki lub reguły świdra. Obracanie punktu przeciwnie do ruchu wskazówek zegara tworzy dodatni moment pędu.

Ponieważ prędkość obrotowa v¯ jest kierowana stycznie do ścieżki kołowej, wyrażenie wektorowe można zapisać w postaci skalarnej:

L = m * v * r.

Moment siły

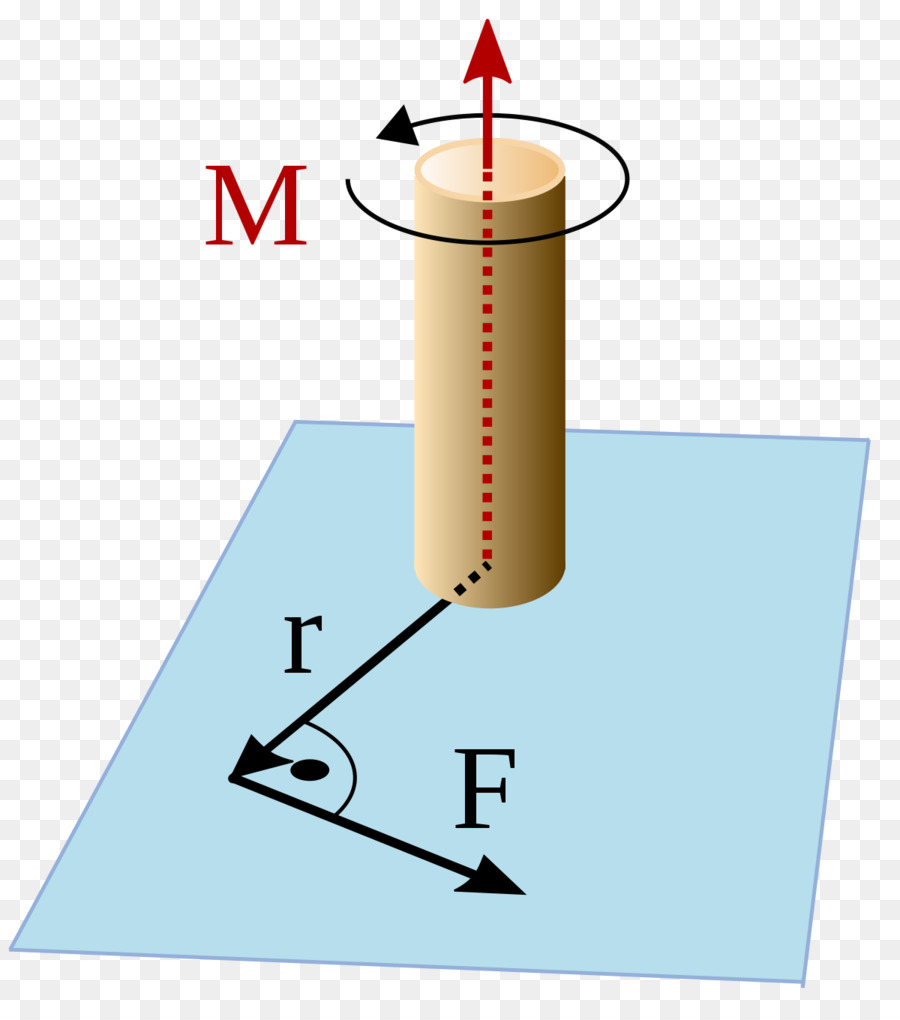
Jest to kolejna ważna cecha ruchu obrotowego. W fizyce wielkość ta jest wprowadzana w ten sam sposób, co moment pędu punktu materialnego, ale zamiast wielkości ruchu należy zastąpić siłę styczną we wzorze opisanym powyżej. Mamy:

M¯ = [r¯ * F¯].

Moment siły, który jest również nazywany momentem obrotowym, charakteryzuje zdolność tego ostatniego do obrócenia układu i nadania jego przyspieszenia kątowego.

Kierunek wektora momentu obrotowego M¯ określają te same zasady, co w przypadku wektora L¯. Jeśli system wykonuje przyspieszony obrót, to M¯ i L¯ pokrywają się w kierunku, jeśli spowolnione, wtedy będą skierowane przeciwnie.

Jeżeli siła F ¯ i wektor promieni r są prostopadłe, to forma wektorowa rekordu zamieni się w podobny skalar:

M = r * F.

Wartość r nazywana jest dźwignią siły. Im większa wartość, tym większy moment, w którym powstaje siła F, a większe przyspieszenie kątowe układu.

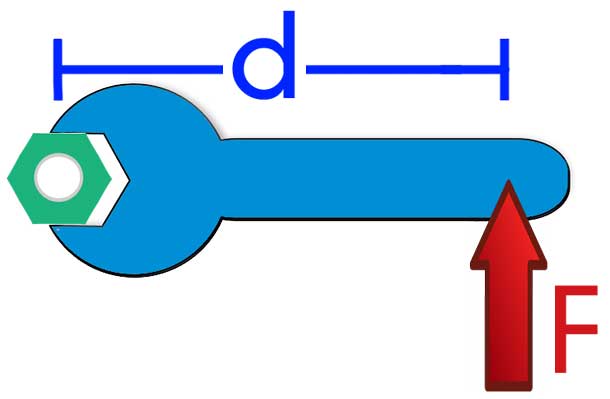
Przykładami, które pozwolą na lepsze zrozumienie znaczenia fizycznego M¯, są odkręcenie nakrętki specjalnym długim kluczem, proces otwierania drzwi z jego pchnięciem w pobliżu uchwytu i przy zawiasach drzwiowych, a także proces utrzymywania ciała o określonej masie na naciągniętej i dociśniętej do ciała ramię.

Moment bezwładności

Pozostaje zdefiniować trzeci punkt, który służy do ilościowego opisania procesu rotacji. Moment bezwładności punktu materialnego, którego parametry zostały zapisane na początku artykułu, oblicza się za pomocą następującego wzoru:

I = m * r ² .

W przeciwieństwie do dwóch pozostałych momentów (M¯ i L¯) moment bezwładności jest skalarem. Za jego pomocą opisano bezwładności systemu (analogia z masą podczas ruchu translacyjnego).

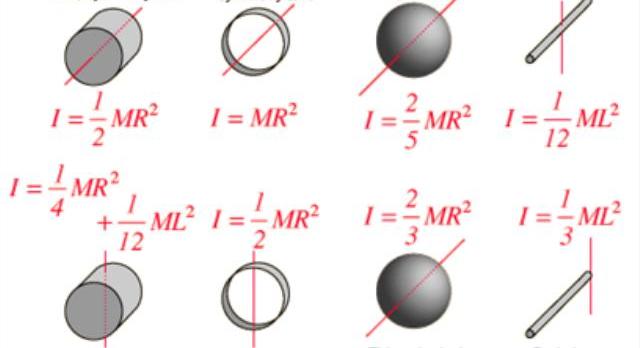
Oczywiście, aby określić wartość I dla ciała stałego o złożonym kształcie i nierównomiernej gęstości, należy użyć liczby całkowitej:

I = ∫ _m (r ² * dm).

W rzeczywistości wzór odzwierciedla sumę wielkości I _i dla każdego punktu materialnego.

Moment bezwładności I jest charakterystyczny nie tylko dla kształtu i rozkładu masy w układzie obrotowym, ale także zależy od położenia osi. Na przykład wielu zauważyło, że o wiele łatwiej jest obracać metalowy pręt lub drewniany mop wzdłuż osi przechodzącej przez ich długość niż wzdłuż prostopadłej osi. W drugim przypadku moment bezwładności nabiera większego znaczenia.

Równanie momentu dla punktu materialnego

Teraz nadszedł czas, aby przejść bezpośrednio do tematu artykułu. Jeżeli moment M działa przez czas dt, wówczas prowadzi do zmiany momentu pędu o wartość dL, czyli:

dL = M * dt.

Ta równość jest różną formą zapisu równania chwili w fizyce. Przenieś termin dt na lewą stronę równości i jawnie przepisuj dL, otrzymamy:

dL / dt = M =>

m * dv * r / dt = M.

Przypomnijmy, że prędkość liniowa w kinemacie jest związana z następującym równaniem kątowym:

v = ω * r.

Zastępując go równaniem chwil, otrzymujemy:

m * dω * r ² / dt = M =>

I * α = M, gdzie α = dω / dt, I = m * r ² .

Uzyskana równość jest często wykorzystywana do wyznaczania kinematycznych charakterystyk układu obrotowego, jeśli znany jest moment sił zewnętrznych M i moment bezwładności I.

Prawo zachowania wartości L

Równanie momentowe pokazuje, w jaki sposób zmienia się moment pędu, gdy działa moment zewnętrzny M. Co stanie się z systemem, jeśli M okaże się zerowe? W takim przypadku wartość L zostanie zapisana. Wzór matematyczny dla tej sytuacji jest zapisany w następujący sposób:

L = const or

L = m * r * v = m * r ² * ω = I * ω = const.

Zwróć uwagę, że warunek M = 0 powinien być spełniony tylko dla sił zewnętrznych. Siły wewnętrzne, które tworzą moment M, nie mogą zmienić momentu pędu układu.

Conservation Law L służy do obracania sztucznych satelitów w kosmosie i na łyżwach. Tak więc, grupując się na różne sposoby, sportowiec zmienia wartość swojego momentu bezwładności, co prowadzi do proporcjonalnej zmiany prędkości jego obrotu kątowego.

Przykładowe zadanie

Siła 10 N działa na punkt materialny o wadze 2 kg Wiedząc, że promień obrotu punktu materialnego wokół osi wynosi 0,5 m, a także biorąc pod uwagę, że siła działa stycznie do trajektorii, konieczne jest znalezienie prędkości kątowej punktu 5 sekund po rozpoczęciu ruchu .

Piszemy równanie momentowe i wyrażamy przyspieszenie α:

I * α = M =>

α = M / I.

Zastępujemy teraz wyrażenia dla M i I, biorąc pod uwagę warunki problemu, mamy:

α = F * r / (m * r ² ) = F / (m * r).

Ponieważ rozważany ruch występuje przy stałym przyspieszeniu α, do obliczenia ω można zastosować następującą formułę:

ω = α * t.

Wstawiając do niego wynikowe wyrażenie dla α, dochodzimy do ostatecznej formuły roboczej:

ω = F * t / (m * r).

Biorąc pod uwagę dane o problemie, możesz napisać odpowiedź: ω = 50 rad / s. Ta wartość odpowiada prawie 8 pełnym obrotom wokół osi na sekundę.