Każde prawo Kirchhoffa jest proste i proste.

Gustav-Robert Kirhof, wybitny niemiecki fizyk i matematyk z XIX wieku, odkrył i sformułował dwa prawa elektrotechniczne nazwane jego imieniem.

Odkrycia Kirchhoffa

Przy całej pozornej prostocie i przejrzystości prawa Kirchhoffa stały się podstawą nowoczesnej nauki i podstawą metod obliczeniowych. Ich praktyczna wartość jest trudna do przeszacowania. Podstawą do badań naukowych profesora Kirchhoffa stały się prawa zachowania ładunku i energii, odkryte wcześniej. Niektórzy eksperci uważają, że bardziej poprawne jest nazywanie praw opisanych przez zasady Kirchhoffa, aby nie mylić ich z innymi niezwykłymi odkryciami tego fizyka dotyczącymi zdolności ciał do promieniowania i absorpcji energii, a także zależności prędkości przepływu. reakcje chemiczne na temperaturę. Jednak w literaturze naukowej i technicznej wciąż używa się terminu "prawo Kirchhoffa", podkreślając w ten sposób zalety tego wielkiego naukowca w dziedzinie inżynierii elektrycznej. A więc jest ich dwóch.

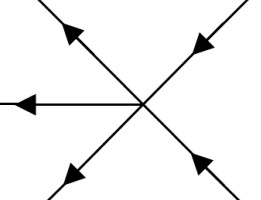
1. Prawo Kirchhoffa w zakresie prądów węzłowych

Węzły w sprzęcie elektrycznym zwane punktem podłączenia przewodów w ilości nie mniejszej niż trzy. Aby zrozumieć efekt Pierwszego Prawa Kirgofa, wystarczy wyobrazić sobie zwykłą wodę. Jeżeli woda jest podawana do jednej z rur, przepływa do pozostałych dwóch. Inna możliwość jest również możliwa, gdy rura odprowadzająca jest jedna, a rura zasilająca ma dwa, ale w każdym razie, ile wody w tee będzie płynąć, tak dużo wypłynie. Teraz zadanie może być skomplikowane, przyznając, że liczba wejść i wyjść w węźle jest arbitralnie duża. Jednak wynik będzie taki sam, ilość płynu przychodzącego i wychodzącego będzie równa, to znaczy w języku matematyki, algebraiczna suma wydatków wynosi zero. Pierwsze prawo Kirchhoffa uważa prądy elektryczne w węzłach, które zachowują się tak samo jak woda w tee. Jeśli występują prądy przychodzące i wychodzące, ich suma, biorąc pod uwagę znak, będzie równa zeru. W tym przypadku wartość prądów wejściowych jest wskazywana dodatnim znakiem "plus", a prądy wyjściowe - ujemnym "minusem". Formuła matematyczna wygląda następująco:

Σ (I in., ... I out.) = 0

gdzie ja w - wielkość napływających prądów ze znakiem "+";

Wyjdę - wielkość wychodzących prądów ze znakiem "-".

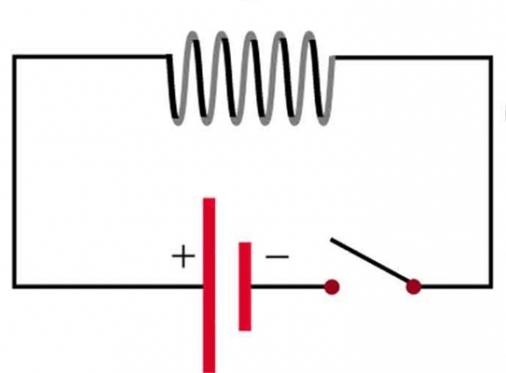
2. Prawo Kirchhoffa dotyczące sumy spadków napięcia

Drugie prawo Kirchhoffa jest nieco trudniejsze do zrozumienia, nie ma takich bezpośrednich i wizualnych skojarzeń, jak pierwsze, ale jest również proste. Na początek powinieneś sobie wyobrazić zamknięte proste obwód elektryczny składający się z źródło zasilania i obciążenie czynne w postaci oporu. Kiedy zaciski wyłącznika są zamknięte, przez rezystor płynie prąd i spadnie całe napięcie zasilające. Zadanie jest ponownie skomplikowane, a wielkość oporu zmienia się. Teraz jest ich dużo i każdy ma inny rozmiar. Kiedy przepływa przez nie prąd elektryczny, będzie on taki sam w obwodzie i zgodnie z prawem Ohma będzie równy źródłowi napięcia podzielonemu przez sumę wszystkich rezystancji. Na każdym z nich spadnie jego część. Tak więc drugie prawo Kirchhoffa stwierdza, że ​​całkowita ilość spadków napięcia na każdej z sekcji obwodu jest równa wartości napięcia zasilania. Innymi słowy, całkowita suma algebraiczna wraz ze źródłem wynosi zero.

Najprostsza formuła matematyczna opisuje drugie prawo Kirchhoffa w następujący sposób:

ΣU c = 0

gdzie U C - spadek napięcia w różnych częściach zamkniętego obwodu elektrycznego (obwodu).