Ekstremalne punkty funkcyjne. Jak znaleźć?
Analiza matematyczna - to dość zabawna sekcja z matematyki, z którą absolutnie wszystkie absolwentki i uczniowie muszą się zmierzyć. Niemniej jednak nie każdy lubi matana. Niektórzy mogą nie rozumieć nawet elementarnych rzeczy, takich jak pozornie standardowe badanie funkcji. Ten artykuł ma na celu naprawienie takiego błędu. Chcesz dowiedzieć się więcej o analizie funkcji? Czy chciałbyś wiedzieć, jakie są punkty ekstremalne i jak je znaleźć? Ten artykuł jest dla Ciebie.
Badanie wykresu funkcji
Przede wszystkim warto zrozumieć, dlaczego analiza wykresu jest konieczna. Są proste funkcje do rysowania, które nie są trudne. Parabola może służyć jako żywy przykład takiej funkcji. Narysuj jej harmonogram nie jest trudne. Wszystko, czego potrzeba, to znaleźć liczby, dla których funkcja przyjmuje wartość za pomocą prostej transformacji, a co do zasady jest to wszystko, co jest konieczne do narysowania, aby narysować wykres paraboli.
Ale co, jeśli funkcja, której wykres musimy narysować, jest znacznie trudniejsza? Ponieważ właściwości złożonych funkcji są raczej niejasne, konieczne jest przeprowadzenie całej analizy. Tylko wtedy funkcja może być przedstawiona graficznie. Jak to zrobić? Odpowiedź na to pytanie można znaleźć w tym artykule.
Plan analizy funkcji
Pierwszą rzeczą, którą należy zrobić, jest przeprowadzenie powierzchownego studium funkcji, podczas której znajdziemy domenę definicji. Zacznijmy więc w kolejności. Domeną definicji jest zbiór wartości, za pomocą których określona jest funkcja. Mówiąc najprościej, są to liczby, które mogą być użyte w funkcji zamiast x. Aby określić zakres, wystarczy spojrzeć na wpis. Na przykład oczywiste jest, że funkcja y (x) = x 3 + x 2 - x + 43 domena definicji jest zbiorem liczb rzeczywistych. Cóż, z funkcją podobną do (x 2 - 2x) / x, wszystko jest trochę inne. Ponieważ liczba w mianowniku nie może wynosić 0, dziedziną funkcji będą wszystkie liczby rzeczywiste, oprócz zera.
Następnie musisz znaleźć tak zwaną funkcję zer. Są to wartości argumentu, dla którego cała funkcja przyjmuje wartości zerowe. Aby to zrobić, konieczne jest zrównanie funkcji do zera, rozważenie jej w szczegółach i wykonanie pewnych transformacji. Weźmy funkcję y (x) = (x 2 - 2x) / x, która jest nam już znana. Z kursu szkolnego wiemy, że ułamek wynosi 0, gdy licznik jest zerowy. Dlatego odrzucamy mianownik i zaczynamy pracę z licznikiem, przyrównując go do zera. Otrzymujemy x 2 - 2x = 0 i wstawiamy x do nawiasów. Stąd x (x - 2) = 0. W rezultacie stwierdzamy, że nasza funkcja wynosi zero, gdy x jest równe 0 lub 2.
Punkty ekstremalne na wykresie funkcji
Podczas badania wykresu funkcji wiele osób napotyka problem w postaci punktów ekstremalnych. I to jest dziwne. W końcu skrajności są dość prostym tematem. Nie wierzysz? Przekonaj się sam, czytając tę część artykułu, w której omówimy punkty minimum i maksimum.
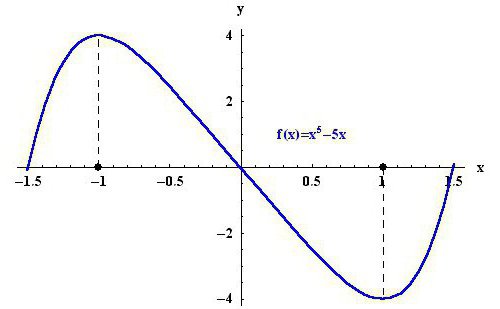
Na początek należy zrozumieć, co stanowi skrajność. Extum to wartość graniczna, którą funkcja osiąga na wykresie. Stąd okazuje się, że istnieją dwie skrajne wartości - maksymalna i minimalna. Dla jasności możesz spojrzeć na obrazek powyżej. Na badanym obszarze punkt -1 jest maksimum funkcji y (x) = x 5 - 5x, a punkt 1, odpowiednio, jest minimum.
Nie myl także koncepcji. Punkty ekstremalne funkcji to argumenty, w których dana funkcja przyjmuje wartości ekstremalne. Z kolei ekstremum jest wartością minimum i maksimum funkcji. Na przykład rozważ ponownie obrazek powyżej. -1 i 1 są punktami ekstremum funkcji, a 4 i -4 są skrajnościami.
Znalezienie ekstremalnych punktów
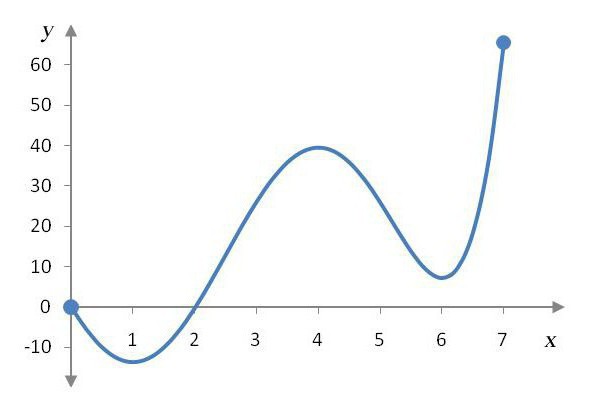
Ale jak można znaleźć punkty ekstremalne funkcji? To całkiem proste. Pierwszą rzeczą do zrobienia jest znalezienie pochodnej równania. Załóżmy, że mamy zadanie: "Znajdź punkty ekstremalne funkcji y (x), x jest argumentem. Dla jasności przyjmujemy funkcję y (x) = x 3 + 2x 2 + x + 54. Rozróżnijmy i otrzymamy następujące równanie: 3x 2 + 4x + 1. W końcu mamy standard równanie kwadratowe. Wszystko, co trzeba zrobić dalej, to zrównanie go do zera i znalezienie korzeni. Ponieważ dyskryminator jest większy od zera (D = 16 - 12 = 4), to równanie jest zdefiniowane przez dwa pierwiastki. Znajdź je i uzyskaj dwie wartości: 1/3 i -1. Będą to ekstremalne punkty funkcji. Jak jednak określić, kto jest kim? Który punkt jest maksymalny i który jest minimalny? Aby to zrobić, weź następny punkt i dowiedz się jego wartości. Na przykład, weź liczbę -2, która jest po lewej stronie linii współrzędnych od -1. Podstawiamy tę wartość do naszego równania y (-2) = 12 - 8 + 1 = 5. W rezultacie otrzymujemy liczbę dodatnią. Oznacza to, że w przedziale od 1/3 do -1 funkcja wzrasta. To z kolei oznacza, że w odstępach od minus nieskończoności do 1/3 i od -1 do plus nieskończoność funkcja maleje. Tak więc możemy wywnioskować, że liczba 1/3 jest minimalnym punktem funkcji na badanym przedziale, a -1 jest punktem maksymalnym.
Suma punktów ekstremalnych funkcji

Warto również zauważyć, że nie tylko trzeba znajdować ekstremalne punkty w USE, ale także wykonywać z nimi jakąś operację (dodawać, mnożyć itp.). Z tego powodu należy zwrócić szczególną uwagę na warunki problemu. W końcu z powodu nieuwagi możesz stracić punkty.