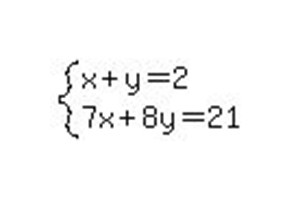Metoda Gaussa do rozwiązywania macierzy. Rozwiązanie układu równań liniowych metodą Gaussa
Od początku XVI-XVIII wieku matematycy zaczęli intensywnie badać funkcje, dzięki którym tak wiele zmieniło się w naszym życiu. Technologia komputerowa bez tej wiedzy po prostu by nie istniała. Aby rozwiązać złożone problemy, stworzono równania i funkcje liniowe, różne koncepcje, twierdzenia i metody rozwiązania. Jedną z takich uniwersalnych i racjonalnych metod i metod rozwiązywania równań liniowych i ich układów była metoda Gaussa. Matryce, ich ranga, determinant - wszystko można obliczyć bez skomplikowanych operacji.
Czym jest slau
W matematyce istnieje pojęcie SLAE - systemu liniowych równań algebraicznych. Jaka ona jest? Jest to zbiór m równań z nieznanymi zmiennymi n nieznany, zwykle oznaczany jako x, y, z lub x 1 , x 2 ... x n lub innymi symbolami. Aby rozwiązać ten system za pomocą metody Gauss, należy znaleźć wszystkie nieznane nieznane. Jeśli system ma taką samą liczbę niewiadomych i równań, wówczas nazywany jest systemem n-tego rzędu.
Ad
Najpopularniejsze metody rozwiązywania slaf
W instytucjach edukacyjnych szkolnictwa średniego uczą się różnych metod rozwiązywania takich systemów. Najczęściej są to proste równania składające się z dwóch niewiadomych, więc każda istniejąca metoda znalezienia odpowiedzi na nie zajmie dużo czasu. Może to być metoda substytucji, gdy inna pochodzi z jednego równania i podstawiona w oryginalną. Lub metodę terminu przez odejmowanie i dodawanie. Ale metoda Gaussa jest uważana za najłatwiejszą i uniwersalną. Umożliwia to rozwiązywanie równań z dowolną liczbą niewiadomych. Dlaczego ta technika jest uważana za racjonalną? To proste. Metoda macierzowa jest dobra, ponieważ nie ma potrzeby przepisywania niepotrzebnych znaków kilka razy jako nieznanych, wystarczy wykonać operacje arytmetyczne na współczynnikach - a otrzymasz wiarygodny wynik.
Ad
Gdzie są stosowane SLAE w praktyce
Rozwiązaniem SLAEs są punkty przecięcia linii na wykresach funkcji. W naszej zaawansowanej technicznie epoce komputerów ludzie, którzy są blisko związani z rozwojem gier i innych programów, muszą wiedzieć, jak rozwiązać takie systemy, co reprezentują i jak sprawdzić poprawność uzyskanego wyniku. Najczęściej programiści opracowują specjalne programy komputerowe dla algebry liniowej, w tym system równań liniowych. Metoda Gaussa pozwala obliczyć wszystkie istniejące rozwiązania. Stosowane są również inne uproszczone formuły i techniki.
Kryterium zgodności SLAU
Taki system można rozwiązać tylko wtedy, gdy jest kompatybilny. Dla jasności reprezentujemy SLAE jako Ax = b. Ma rozwiązanie, jeśli zadzwonił (A) równy dzwonek (A, b). W tym przypadku (A, b) jest matrycą typu rozszerzonego, którą można uzyskać z macierzy A przez przepisanie jej na wolne elementy. Okazuje się, że rozwiązanie równania liniowe Metoda Gaussa jest dość łatwa.
Być może jakaś notacja nie jest całkowicie jasna, więc na przykład trzeba spojrzeć na wszystko. Załóżmy, że istnieje system: x + y = 1; 2x-3y = 6. Składa się z tylko dwóch równań, w których 2 są nieznane. System będzie miał rozwiązanie tylko wtedy, gdy ranga jego macierzy będzie równa rangi rozwiniętej macierzy. Jaka jest ranga? Jest to liczba niezależnych linii systemu. W naszym przypadku ranga matrycy wynosi 2. Macierz A będzie się składać ze współczynników znajdujących się w pobliżu niewiadomych, a współczynniki za znakiem "=" również pasują do rozszerzonej macierzy.
Ad
Dlaczego SLAE może być reprezentowany w postaci macierzy
W oparciu o kryterium zgodności według sprawdzonego twierdzenia Kroneckera-Capellego, układ liniowych równań algebraicznych można przedstawić w postaci macierzowej. Korzystając z metody kaskadowej Gaussa, możesz rozwiązać macierz i uzyskać jedyną niezawodną odpowiedź na cały system. Jeśli ranga zwykłej macierzy jest równa jej rozwiniętej macierzy, ale jest mniejsza niż liczba niewiadomych, to system ma nieskończoną liczbę odpowiedzi.
Transformacje macierzy
Przed przystąpieniem do rozwiązania macierzy należy wiedzieć, jakie działania można wykonać na ich elementach. Istnieje kilka elementarnych przekształceń:
- Zmieniając system na widok macierzy i wdrażając jego rozwiązanie, możliwe jest pomnożenie wszystkich elementów wiersza przez ten sam współczynnik.
- Aby przekształcić matrycę w formę kanoniczną, można zamienić dwa równoległe wiersze. Forma kanoniczna oznacza, że wszystkie elementy macierzy, które znajdują się na głównej przekątnej, stają się jednostkami, a pozostałe - zerami.
- Odpowiednie elementy równoległych rzędów macierzy można dodać jeden do drugiego.
Metoda Jordana-Gaussa
Istotą rozwiązywania układów liniowych równań homogenicznych i niejednorodnych metodą Gaussa jest stopniowe eliminowanie niewiadomych. Załóżmy, że mamy układ dwóch równań, w których występują dwie niewiadome. Aby je znaleźć, musisz sprawdzić system pod kątem kompatybilności. Równanie metodą Gaussa rozwiązuje się bardzo prosto. Konieczne jest zapisanie współczynników znajdujących się w pobliżu każdego nieznanego w widoku macierzy. Aby rozwiązać system, musisz napisać rozszerzoną macierz. Jeśli jedno z równań zawiera mniejszą liczbę niewiadomych, to konieczne jest wstawienie "0" zamiast brakującego elementu. Wszystkie znane metody transformacji są stosowane do macierzy: mnożenie, dzielenie przez liczbę, dodawanie odpowiednich elementów wierszy do siebie i innych. Okazuje się, że w każdym rzędzie konieczne jest pozostawienie jednej zmiennej o wartości "1", reszta prowadzi do postaci zerowej. Aby uzyskać dokładniejsze zrozumienie, konieczne jest rozważenie metody Gaussa za pomocą przykładów.
Prosty przykład rozwiązania systemowego 2x2.
Najpierw przyjmujemy prosty układ równań algebraicznych, w którym będą 2 niewiadome.
Przepisz go do rozwiniętej macierzy.
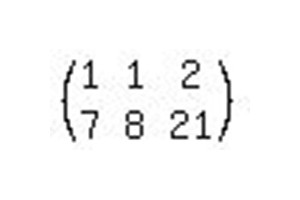
Aby rozwiązać ten układ równań liniowych, wymagane jest wykonanie tylko dwóch operacji. Musimy doprowadzić matrycę do formy kanonicznej, aby jednostki stały wzdłuż głównej przekątnej. Tak więc, przenosząc z widoku macierzy z powrotem do systemu, otrzymujemy równania: 1x + 0y = b1 i 0x + 1y = b2, gdzie b1 i b2 są wynikowymi odpowiedziami w procesie rozwiązania.
Ad

- Pierwszym krokiem w rozwiązaniu rozwiniętej macierzy byłby: pierwszy wiersz musi być pomnożony przez -7, a odpowiednie elementy dodane do drugiego rzędu, odpowiednio, aby pozbyć się jednego nieznanego w drugim równaniu.
- Ponieważ rozwiązanie równań metodą Gaussa oznacza redukcję macierzy do postaci kanonicznej, konieczne jest wykonanie tych samych operacji z pierwszym równaniem i usunięcie drugiej zmiennej. Aby to zrobić, odejmujemy drugą linię od pierwszej i otrzymujemy niezbędną odpowiedź - rozwiązanie SLAU. Lub, jak pokazano na rysunku, druga linia jest mnożona przez współczynnik -1, a elementy drugiego rzędu dodawane są do pierwszej linii. To jest to samo.
Jak widać, nasz system rozwiązuje metoda Jordan-Gauss. Przepisujemy go na wymaganą formę: x = -5, y = 7.
Ad
Przykład rozwiązania SLAE 3x3
Załóżmy, że mamy bardziej złożony układ równań liniowych. Metoda Gaussa pozwala obliczyć odpowiedź nawet dla pozornie mylącego systemu. Dlatego, aby uzyskać głębszy wgląd w metodę obliczeń, można przejść do bardziej złożonego przykładu z trzema niewiadomymi.
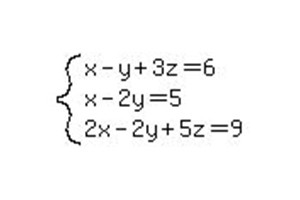
Podobnie jak w poprzednim przykładzie, przepisujemy system w postaci rozwiniętej macierzy i zaczynamy ją redukować do postaci kanonicznej.
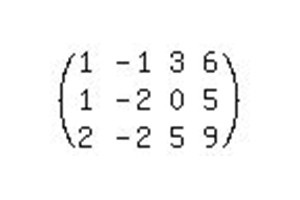
Aby rozwiązać ten system, musisz wykonać znacznie więcej kroków niż w poprzednim przykładzie.
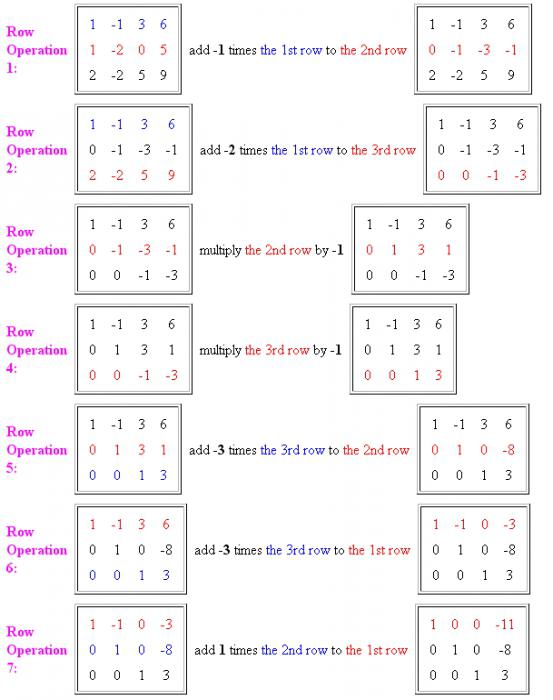
- Najpierw musisz wykonać w pierwszej kolumnie jeden element jednostki i pozostałe zera. Aby to zrobić, pomnóż pierwsze równanie przez -1 i dodaj do niego drugie równanie. Ważne jest, aby pamiętać, że przepisujemy pierwszy wiersz w jego oryginalnej formie, a drugi w zmodyfikowanym.
- Następnie usuń tę samą pierwszą nieznaną z trzeciego równania. W tym celu elementy pierwszego rzędu mnoży się przez -2 i dodaje je do trzeciego rzędu. Teraz pierwsza i druga linia zostały przepisane w oryginalnej formie, a trzecia - już ze zmianami. Jak widać z wyniku, uzyskaliśmy pierwszą jednostkę na początku głównej przekątnej macierzy i pozostałe zera. Jeszcze więcej akcji, a układ równań za pomocą metody Gaussa będzie niezawodnie rozwiązany.
- Teraz konieczne jest wykonywanie operacji na innych elementach wierszy. Trzecie i czwarte działanie można połączyć w jedno. Konieczne jest podzielenie drugiej i trzeciej linii przez -1, aby pozbyć się jednostek ujemnych po przekątnej. Trzecia linia, którą już doprowadziliśmy do niezbędnego formularza.
- Następnie wprowadzamy drugą linię do formy kanonicznej. Aby to zrobić, mnożymy elementy trzeciego rzędu przez -3 i dodajemy je do drugiego rzędu macierzy. Wynik pokazuje, że druga linia jest również zredukowana do postaci, której potrzebujemy. Pozostaje wykonać kilka operacji i usunąć współczynniki niewiadomych z pierwszego rzędu.
- Aby zrobić 0 z drugiego elementu linii, konieczne jest pomnożenie trzeciej linii przez -3 i dodanie jej do pierwszego wiersza.
- Kolejnym ważnym krokiem będzie dodanie do pierwszej linii niezbędnych elementów drugiego rzędu. Otrzymujemy więc kanoniczną formę matrycy, a zatem odpowiedź.
Jak widać, rozwiązanie równań metodą Gaussa jest dość proste.
Przykład rozwiązania układu równań 4x4
Niektóre bardziej złożone układy równań można rozwiązać metodą Gaussa za pomocą programów komputerowych. Konieczne jest wprowadzenie do istniejących pustych komórek współczynników z niewiadomymi, a sam program krok po kroku obliczy konieczny wynik, szczegółowo opisując każde działanie.
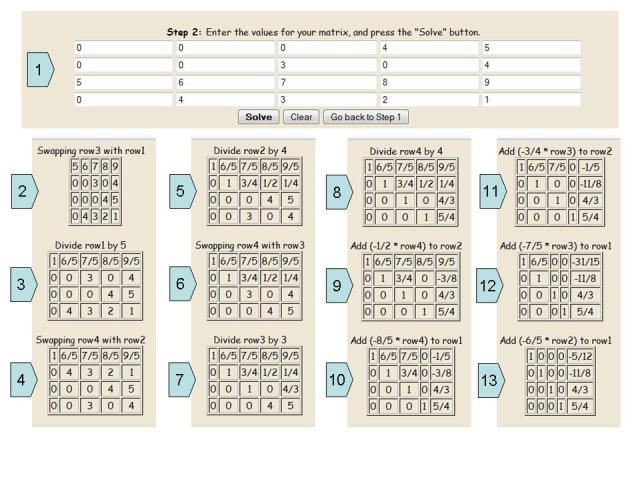
Poniżej znajduje się instrukcja krok po kroku do rozwiązania takiego przykładu.
• W pierwszym kroku wolne współczynniki i liczby o nieznanych wartościach pasują do pustych komórek. Tak więc okazuje się ta sama rozszerzona matryca, którą piszemy ręcznie.
• Następnie wszystkie linie są odwrócone, aby elementy jednostkowe mogły być wyrażone wzdłuż głównej przekątnej.
• Wszystkie niezbędne operacje arytmetyczne są wykonywane w celu dostosowania rozwiniętej macierzy do postaci kanonicznej. Należy rozumieć, że odpowiedź na układ równań nie zawsze jest taka sama - są to liczby całkowite. Czasami rozwiązanie może pochodzić z liczb ułamkowych.
Rozwiązanie weryfikacji
Metoda Jordan-Gauss zapewnia weryfikację poprawności wyniku. Aby dowiedzieć się, czy współczynniki są poprawnie obliczone, konieczne jest tylko zastąpienie wyniku w oryginalnym układzie równań. Lewa strona równania musi odpowiadać prawej stronie, która znajduje się za znakiem równości. Jeśli odpowiedzi nie są zgodne, musisz ponownie obliczyć system lub spróbować zastosować do niego inną metodę rozwiązania SLAE, znaną Ci jako substytucję lub odejmowanie i dodawanie. W końcu matematyka jest nauką, która ma ogromną liczbę różnych technik rozwiązywania. Ale pamiętaj: wynik musi być zawsze taki sam, bez względu na zastosowaną metodę rozwiązania.
Metoda Gaussa: Najczęstsze błędy podczas rozwiązywania SLAE
Przy rozwiązywaniu układów liniowych równań najczęściej występują błędy takie jak nieprawidłowe przenoszenie współczynników do postaci macierzy. Istnieją systemy, w których niektóre niewiadome są nieobecne w jednym z równań, a następnie przekazując dane do rozwiniętej macierzy, mogą one zostać utracone. W rezultacie, podczas rozwiązywania tego układu, wynik może nie odpowiadać rzeczywistemu.
Kolejnym jednym z głównych błędów może być niepoprawne zapisanie wyniku końcowego. Konieczne jest jasne zrozumienie, że pierwszy współczynnik będzie odpowiadał pierwszemu nieznanemu z systemu, drugi do drugiego, i tak dalej.
Metoda Gaussa opisuje szczegółowo rozwiązanie równań liniowych. Dzięki niemu można łatwo wykonać niezbędne operacje i znaleźć właściwy wynik. Ponadto jest uniwersalnym narzędziem do znalezienia wiarygodnej odpowiedzi na równania o dowolnej złożoności. Może dlatego tak często jest używany w rozwiązywaniu SLAE.