W jaki sposób sformułowane i udowodnione jest twierdzenie cosinus?
Nie wszyscy uczniowie, a jeszcze bardziej dorośli, wiedzą, że twierdzenie o kosinusie jest bezpośrednio związane z twierdzeniem Pitagorasa. Dokładniej, ten drugi przypadek jest szczególnym przypadkiem pierwszego. Ten moment, a także dwa sposoby udowodnienia twierdzenia cosinusa, pomogą ci stać się osobą bardziej kompetentną. Ponadto praktyka wyrażania wartości z oryginalnych wyrażeń jest dobrze rozwiniętym logicznym myśleniem. Długa formuła badanego twierdzenia z pewnością zmusi do pracy i poprawy.
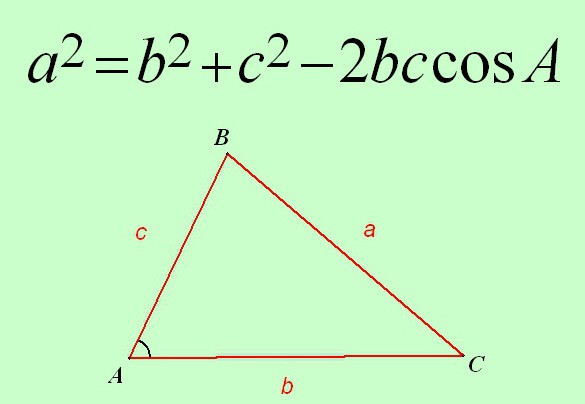
Początek konwersacji: wprowadzenie symboli
To twierdzenie jest sformułowane i udowodnione dla dowolnego trójkąta. Dlatego zawsze można go użyć w każdej sytuacji, jeśli podane są dwie strony, aw niektórych przypadkach trzy i kąt, a niekoniecznie między nimi. Cokolwiek rodzaj trójkąta twierdzenie zawsze działa.
A teraz o oznaczaniu ilości we wszystkich wyrażeniach. Lepiej się zgodzić od razu, żeby nie wyjaśniać tego kilka razy. W tym celu skompilowano poniższą tabelę.
| Element trójkąta | Jego oznaczenie |
| Nieznana strona | a |
| Dwie inne strony | w, z |
| Kąt naprzeciwko nieznanej strony | A |
| Kąty, które leżą przeciw innym stronom | B, C |
| Wysokość wierzchołka trójkąta | n |
Formułowanie i pisanie matematyczne
Twierdzenie cosinusa sformułowane jest w następujący sposób:
Kwadrat boku dowolnego trójkąta jest równy sumie kwadratów pozostałych dwóch boków, minus dwukrotność iloczynu tych samych boków przez cosinus kąta leżącego między nimi.
Oczywiście, to jest długie, ale jeśli zrozumiesz jego istotę, to będzie to łatwe do zapamiętania. Możesz sobie nawet wyobrazić rysunek trójkąta. Wizualnie zawsze łatwiejsze do zapamiętania.
Wzór tego twierdzenia będzie wyglądał następująco:
a 2 = 2 + s 2 - 2 * c * s * cos A.
Trochę długo, ale wszystko jest logiczne. Jeśli spojrzysz trochę bliżej, zobaczysz, że litery są powtarzane, więc łatwo je zapamiętać.
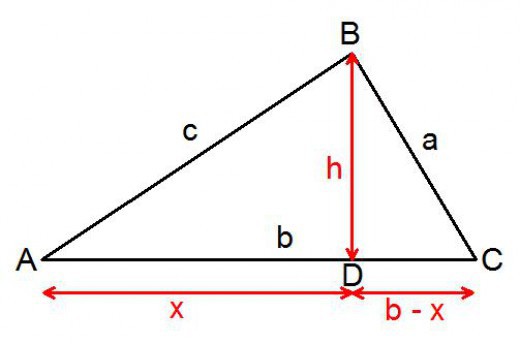
Wspólny dowód twierdzenia
Ponieważ jest on ważny dla wszystkich trójkątów, możliwe jest wybranie uzasadnienia dowolnego typu. Niech to będzie postać ze wszystkimi ostrymi kątami. Rozważmy dowolny ostry trójkąt, którego kąt C jest większy niż kąt B. Z wierzchołka o tak dużym kącie musisz obniżyć prostopadle do przeciwnej strony. Trzymana wysokość dzieli trójkąt na dwa prostokąty. Jest to wymagane do dowodu.
Strona zostanie podzielona na dwa segmenty: x, y. Muszą być wyrażone w znanych terminach. Część, która okazuje się być w trójkącie z przeciwprostokątną równą, zostanie wyrażona poprzez napisanie:
x = w * cos A.
Drugi będzie równy tej różnicy:
y = s - in * cos A.
Teraz musimy napisać twierdzenie Pitagorasa o dwóch wynikach prawe trójkąty przyjmując nieznaną wysokość. Te formuły będą wyglądać tak:
n 2 = w 2 - (w * cos А) 2 ,
n 2 = a 2 - (c - c * cos A) 2 .
W tych równościach są identyczne wyrażenia po lewej stronie. Dlatego ich prawa strony będą równe. Łatwo jest pisać. Teraz musisz otworzyć nawiasy:
w 2 - w 2 * (cos А) 2 = a 2 - с 2 + 2 с * in * cos А - w 2 * (cos А) 2 .
Jeśli dokonamy przeniesienia i redukcji takich warunków, otrzymamy wstępną formułę, która jest napisana po sformułowaniu, czyli twierdzeniu cosinus. Dowód jest kompletny.
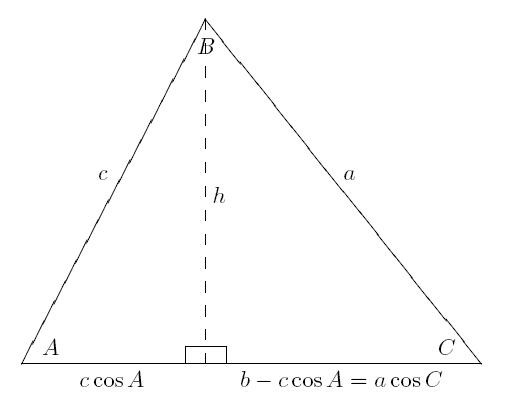
Dowód twierdzenia przez wektory
Jest znacznie krótszy niż poprzedni. A jeśli znasz własności wektorów, to twierdzenie cosinusa dla trójkąta zostanie po prostu udowodnione.
Jeśli boki a, b, c są oznaczane odpowiednio przez wektory BC, AC i AB, wówczas równość jest prawdziwa:
SU = AC - AB.
Teraz musisz wykonać pewne czynności. Pierwszym z nich jest wyrównanie obu stron równości:
BC 2 = AC 2 + AB 2 - 2 AC * AB.
Następnie równość musi zostać przepisana w formie skalarnej, biorąc pod uwagę, że iloczyn wektorów jest równy cosinusowi kąta między nimi a ich wartościami skalarnymi:
BC 2 = AC 2 + AB 2 - 2 AC * AB * cos A.
Pozostaje tylko powrócić do starej notacji, a znowu twierdzenie cosinusa okaże się:
a 2 = 2 + s 2 - 2 * c * s * cos A.
Wzory na inne strony i wszystkie kąty
Aby znaleźć stronę, z twierdzenia cosinusa, które musisz wyodrębnić pierwiastek kwadratowy. Wzór na kwadraty jednej z pozostałych stron będzie wyglądał następująco:
z 2 = a 2 + do 2 - 2 * a * do * cos C.
Aby zapisać wyrażenie dla kwadratu strony, konieczne jest zastąpienie poprzedniej równości wartością od do, i na odwrót, i ustawieniem kąta B pod cosinusem
Z podstawowej formuły twierdzenia możemy wyrazić wartość cosinusa kąta A:
cos А = (w 2 + с 2 - а 2 ) / (2 ¢ * Ń).
Wzory na inne kąty wywodzą się w ten sam sposób. To jest dobra praktyka, więc możesz spróbować napisać je samemu.
Naturalnie nie ma potrzeby zapamiętywania tych formuł. Wystarczy zrozumieć twierdzenie i umiejętność wyprowadzenia tych wyrażeń z głównego zapisu.
Oryginalna formuła twierdzenia pozwala znaleźć stronę, jeśli kąt nie jest pomiędzy dwoma znanymi. Na przykład musisz znaleźć w , gdy podane wartości: a, c, a . Lub nie jest znane, ale są wartości a, b, a .
W tej sytuacji musisz przenieść wszystkie formuły addendum po lewej stronie. Ta równość jest uzyskiwana:
с 2 - 2 * ¢ * с * cos А + в 2 - а 2 = 0.
Przepisz go w nieco innej formie:
z 2 - (2 * w * cos А) * z + (w 2 - i 2 ) = 0.
Możesz łatwo zobaczyć równanie kwadratowe. W nim nieznana ilość to c , a wszystkie pozostałe są podane. Dlatego wystarczy rozwiązać za pomocą dyskryminatora. Więc nieznana strona zostanie znaleziona.
Podobnie otrzymuje się wzór na drugą stronę:
2 - (2 * s * cos A) * c + (c 2 - a 2 ) = 0.
Z innych wyrażeń takie wzory są również łatwe do zdobycia.
Jak obliczyć kąt bez obliczania cosinusa?
Jeśli przyjrzysz się formule kąta kosinusów uzyskanej wcześniej, zauważysz:
- mianownik ułamka jest zawsze liczbą dodatnią, ponieważ zawiera iloczyn boków, które nie mogą być ujemne;
- kąt będzie zależeć od znaku licznika.
Kąt A będzie:
- ostry w sytuacji, gdy licznik jest większy od zera;
- tępe, jeśli to wyrażenie jest negatywne;
- bezpośrednio, gdy jest zero.
Nawiasem mówiąc, ta ostatnia sytuacja zamienia twierdzenie cosinusa na twierdzenie Pitagorasa. Ponieważ dla kąta 90º jego cosinus wynosi zero, a ostatni termin znika.
Pierwsze zadanie
Stan
Kąt rozwarty jakiegoś arbitralnego trójkąta wynosi 120º. O bokach, do których jest ograniczona, wiadomo, że jedna z nich jest o 8 cm dłuższa od drugiej, znana jest długość trzeciej strony, wynosi ona 28 cm, wymagane jest znalezienie obwodu trójkąta.
Rozwiązanie
Najpierw musisz wyznaczyć jedną ze stron literą "x". W takim przypadku drugi będzie równy (x + 8). Ponieważ istnieją wyrażenia dla wszystkich trzech stron, możesz użyć wzoru, który daje twierdzenie cosinus:
28 2 = (x + 8) 2 + x 2 - 2 * (x + 8) * x * cos 120º.
W tabelach cosinusów musisz znaleźć wartość odpowiadającą 120 stopni. Będzie to liczba 0.5 ze znakiem minus. Teraz należy otworzyć nawiasy, przestrzegając wszystkich zasad i podać podobne warunki:
784 = x 2 + 16x + 64 + x 2 - 2x * (-0,5) * (x + 8);
784 = 2x 2 + 16x + 64 + x 2 + 8x;
3x 2 + 24x - 720 = 0.
To równanie kwadratowe rozwiązuje się przez znalezienie wyróżnika, który będzie równy:
D = 24 2 - 4 * 3 * (- 720) = 9216.
Ponieważ jego wartość jest większa od zera, równanie ma dwie podstawowe odpowiedzi.
x 1 = ((-24) + √ (9216)) / (2 * 3) = 12;
x 2 = ((-24) - √ (9216)) / (2 * 3) = -20.
Ostatni root nie może być odpowiedzią na problem, ponieważ partia musi koniecznie być pozytywna.
Więc obie strony są znane. Łatwo znaleźć trzeci: 12 + 8 = 20 (cm). Teraz możesz odpowiedzieć na pytanie o problem. Obwód trójkąta jest zdefiniowany jako suma wszystkich stron:
24 + 12 + 20 = 60 (cm).
Odpowiedź : obwód wynosi 60 centymetrów.

Numer problemu 2
Stan
W trójkącie są znane: c , równe 2 cm; a , który wynosi 10 cm; wartość kąta C 120º. Wymagany do znalezienia strony w .
Rozwiązanie
Najpierw musisz użyć twierdzenia cosinus i wyprowadzić formułę równanie kwadratowe w którym wartość w woli będzie nieznana:
z 2 = a 2 + w 2 - 2 * a * w * cos C
i
w 2 - (2 * a * cos C) * w + (a 2 - c 2 ) = 0.
Konieczne jest zastąpienie wszystkich znanych wartości w warunku:
w 2 - (2 * 10 * cos 120º) * w + (10 2 - 2 2 ) = 0.
Teraz musimy policzyć, co jest możliwe, aby uprościć wyrażenie:
w 2 - (20 * (-1/2)) * w + (100 - 4) = 0
lub
w 2 + 10 * w - 96 = 0.
Jest to standardowe równanie kwadratowe, które należy rozwiązać poprzez znalezienie dyskryminatora:
D = (10) 2 - 4 * 1 * (-96) = 484.
Zgodnie ze wzorami, musisz wykonać obliczenia dla nieznanej strony:
w 1 = (- 10 + 22) / 2 = 6 (cm);
w 2 = (- 10 - 22) / 2 = - 16 - ten root nie spełnia rozwiązania problemu, ponieważ strona nie może być ujemna.
Odpowiedź: nieznana strona ma 6 cm.
Trzecie zadanie
Stan
W niektórych trójkątach podane są boki: a, b, c , które mają odpowiednio 6 cm, 10 cm i 8 cm, wymagane jest obliczenie kąta A.
Rozwiązanie
Ponownie musisz użyć twierdzenia cosinus. Wykorzystuje się jego zapis, w którym znajduje się cosinus kąta A, ponieważ właśnie to należy obliczyć. Oto wzór na cosinus o nieznanym kącie:
cos А = (w 2 + с 2 - а 2 ) / (2 ¢ * Ń).
Pozostaje zastąpić wartości stron i wykonać wszystkie obliczenia:
cos A = (10 2 + 8 2 - 6 2 ) / (2 * 8 * 10).
Po tym jak wszystkie terminy są podniesione do kwadratu i pomnożenie liczb od mianownika:
cos A = (100 + 64 - 36) / (160).
Po dodaniu i podziale okazuje się:
cos A = 128/160 = 0,8.
Teraz musisz użyć tabeli Bradisa, aby dowiedzieć się, jaki kąt jest równy A. Najbliższa wartość kąta dla tego cosinusu wynosi 36º54 '.
Odpowiedź: wartość kąta A wynosi 36º54'.