Jak obliczyć granice sekwencji?
Matematyka jest nauką, która buduje świat. Jako naukowiec i prosta osoba - nikt nie może się bez niej obejść. Po pierwsze, małe dzieci uczą się liczyć, a następnie dodawać, odejmować, mnożyć i dzielić, oznaczenia literowe wchodzą w grę w liceum, a w starszym nie mogą się bez nich obyć.
Ale dzisiaj porozmawiamy o tym, na czym opiera się cała znana matematyka. W społeczności liczb zwanych "limitami sekwencji".
Czym są sekwencje i gdzie jest ich limit?
Znaczenie słowa "sekwencja" nie jest trudne do zinterpretowania. Jest to konstrukcja rzeczy, w których ktoś lub coś jest ułożone w określonej kolejności lub kolejce. Na przykład kolejka do biletów do zoo - jest sekwencją. I może być tylko jeden! Jeśli, na przykład, przyjrzeć się kolejce w sklepie - jest to jedna sekwencja. A jeśli jedna osoba nagle opuści tę linię, to jest kolejna linia, kolejna kolejność.
Słowo "limit" można łatwo zinterpretować - to koniec czegoś. Jednak w matematyce granicami sekwencji są te wartości na linii liczb, do której dąży sekwencja liczb. Dlaczego szuka i nie kończy? Wszystko jest proste, linia liczbowa nie ma końca, a większość sekwencji, takich jak promienie, ma tylko początek i wygląda tak:
x 1 , x 2 , x 3 , ... x n ...
Stąd definicja sekwencji jest funkcją naturalnego argumentu. W prostszych słowach jest to seria członków jakiegoś zbioru.
Jak zbudowana jest sekwencja numeryczna?
Najprostszy przykład sekwencji liczbowej może wyglądać tak: 1, 2, 3, 4, ... n ...
W większości przypadków, z przyczyn praktycznych, sekwencje są zbudowane z liczb, a każdy następny element serii, oznaczony przez X, ma swoją własną nazwę. Na przykład:
x 1 - pierwszy członek sekwencji;
x 2 - drugi członek sekwencji;
x 3 - trzeci członek;
...
x n to n -ty termin.
W praktycznych metodach sekwencję podaje wzór ogólny, w którym występuje pewna zmienna. Na przykład:
X n = 3n, wtedy sama seria liczb będzie wyglądać następująco:
x 1 = 3;
x 2 = 6;
x 3 = 9;
i tak dalej
Nie należy zapominać, że w ogólnym zapisie sekwencji można używać dowolnych łacińskich liter, nie tylko X. Na przykład: y, z, k itd.
Postęp arytmetyczny jako część sekwencji
Zanim przejdziemy do granic ciągów, wskazane jest głębiej zagłębić się w samą koncepcję takiej serii liczbowej, którą wszyscy napotkali będąc w klasach średnich. Postęp arytmetyczny to ciąg liczb, w którym różnica między sąsiednimi członami jest stała.
Zadanie: "Niech 1 = 15, a krok postępu szeregu liczbowego d = 4. Zbuduj pierwszych 4 członków tej serii. "
Rozwiązanie: 1 = 15 (według warunku) - pierwszy członek progresji (seria liczbowa).
a 2 = 15 + 4 = 19 jest drugim członkiem progresji.
i 3 = 19 + 4 = 23 - trzeci członek.
a 4 = 23 + 4 = 27 to czwarty członek.
Jednak ta metoda jest trudna do osiągnięcia dużych wartości, takich jak 125 .. Zwłaszcza w takich przypadkach uzyskano formułę wygodną do ćwiczenia: a n = a 1 + d (n - 1). W tym przypadku 125 = 15 + 4 (125-1) = 511.
Rodzaje sekwencji
Większość sekwencji jest nieskończona, warto ją zapamiętać na całe życie. Istnieją dwa interesujące typy serii liczbowych. Pierwszy jest podany za pomocą wzoru a n = (- 1) n . Matematycy często nazywają tę sekwencję flasher. Dlaczego? Sprawdź jego serię numeryczną.
-1, 1, -1, 1, -1, 1 itd. Przy takim przykładzie staje się jasne, że liczby w sekwencjach można łatwo powtarzać.
Sekwencja czynnikowa. Łatwo zgadnąć - silnia jest obecna w formule definiującej sekwencję. Na przykład: a n = (n + 1)!
Następnie sekwencja będzie wyglądać następująco:
a 1 = 1x2 = 2;
a 2 = 1x2x3 = 6;
a 3 = 1x2x3x4 = 24 itd.
Sekwencja określona przez postęp arytmetyczny nazywana jest nieskończenie malejącą, jeśli nierówność -1 jest obserwowana dla wszystkich jej członków.
a 1 = - ½;
a 2 = ¼;
a 3 = - 1/8 itd.
Istnieje nawet sekwencja składająca się z tej samej liczby. Zatem n = 6 składa się z nieskończonego zbioru szóstek.
Określanie limitu sekwencji
Limity sekwencji od dawna istnieją w matematyce. Oczywiście zasłużyli sobie na własny, kompetentny projekt. Czas więc poznać definicję granic sekwencji. Po pierwsze, rozważ szczegółowo ograniczenie funkcji liniowej:
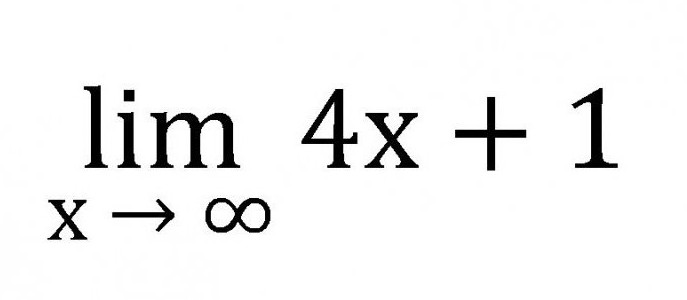
- Wszystkie ograniczenia są ograniczone w skrócie.
- Zapis limitu składa się ze skrótu lim, pewnej zmiennej zmierzającej do pewnej liczby, zera lub nieskończoności, a także od samej funkcji.
Łatwo zrozumieć, że definicję limitu sekwencji można sformułować w następujący sposób: jest to pewna liczba, do której wszyscy członkowie sekwencji nieskończenie się zbliżają. Prosty przykład: a x = 4x + 1. Wtedy sama sekwencja będzie wyglądać tak.
5, 9, 13, 17, 21 ... x ...
Tak więc, ta sekwencja będzie wzrastać w nieskończoność, a zatem jej granica jest równa nieskończoności jako x → ∞, a to powinno być napisane w następujący sposób:
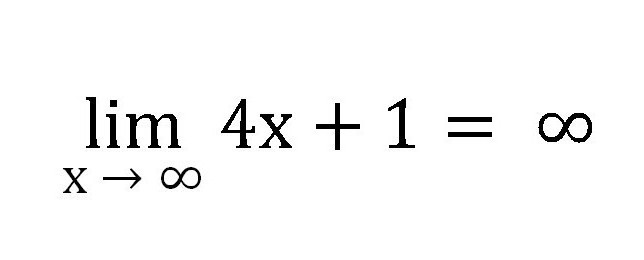
Jeśli weźmiemy podobną sekwencję, ale x będzie miało tendencję do 1, otrzymamy:
a x = 4x + 1.
Cykl liczb będzie następujący: 1.4, 1.8, 4.6, 4.944 i tak dalej. Za każdym razem musisz zastąpić liczbę większą i zbliżoną do jednej (0,1, 0,2, 0,9, 0,986). Z tej serii jasno wynika, że limit funkcji wynosi pięć.
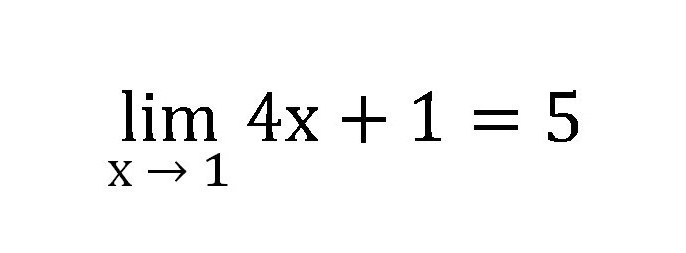
Z tej części warto zapamiętać, jaka jest granica kolejności liczbowej, definicja i metoda rozwiązywania prostych zadań.
Ogólne oznaczenie granicy ciągów
Po zbadaniu granicy sekwencji liczbowej, jej definicji i przykładów możemy przejść do bardziej złożonego tematu. Absolutnie wszystkie granice sekwencji można sformułować za pomocą jednej formuły, która jest zwykle analizowana w pierwszym semestrze.
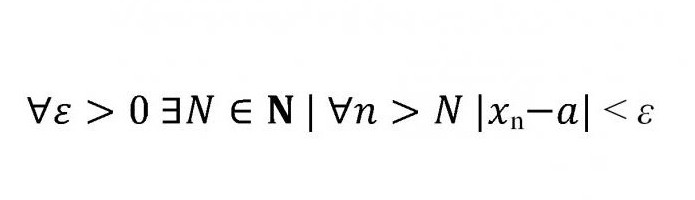
Co oznacza ten zbiór liter, modułów i znaków nierówności?
∀ - Kwantyfikator uniwersalności, zastępujący frazy "dla wszystkich", "dla wszystkich" itp.
∃ - Kwantyfikator istnienia, w tym przypadku oznacza, że istnieje pewna wartość N należąca do zbioru liczby naturalne.
Długi pionowy drążek, następujący po N, oznacza, że dany zbiór N jest "taki, który". W praktyce może oznaczać "takie, że", "takie które" itp.
Dalej jest moduł. Oczywiście moduł jest odległością, która z definicji nie może być ujemna. Więc moduł różnicy jest ściśle mniejszy niż "epsilon".
Aby skonsolidować materiał, przeczytaj formułę na głos.
Niepewność i definitywność limitu
Metoda znajdowania limitu sekwencji, o której była mowa powyżej, jest prosta w użyciu, ale nie tak racjonalna w praktyce. Spróbuj znaleźć ograniczenie dla takiej funkcji:
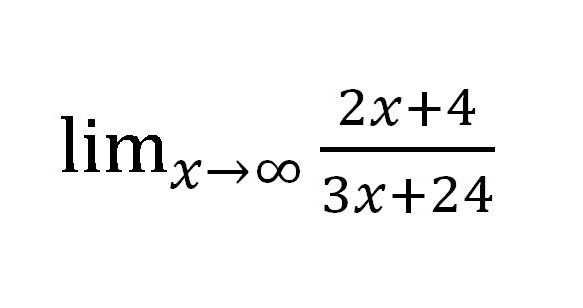
Jeśli podstawimy różne wartości "X" (za każdym razem wzrastając: 10, 100, 1000 itd.), To w liczniku otrzymamy ∞, ale w mianowniku również ∞. Okazuje się dość dziwny ułamek: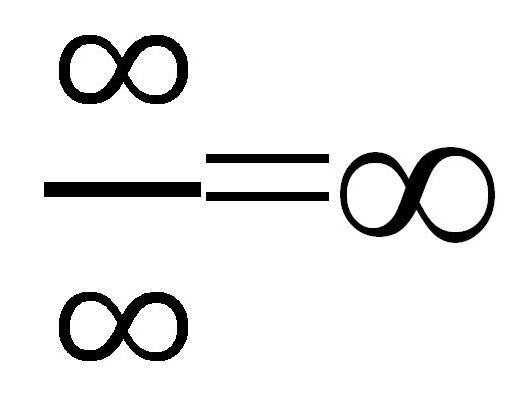 
Ale czy to naprawdę? Obliczyć granicę sekwencji liczbowej w tym przypadku wydaje się dość łatwe. Byłoby możliwe pozostawienie wszystkiego takim, jakie jest, ponieważ odpowiedź jest gotowa i została przyjęta na rozsądnych warunkach, ale jest inna metoda specjalnie dla takich przypadków.
Na początek znajdujemy najwyższą moc w liczniku ułamka - jest to 1, ponieważ x można przedstawić jako x 1 .
Teraz znajdujemy najwyższą moc w mianowniku. Również 1.
Dzielimy licznik i mianownik na zmienną w najwyższym stopniu. W tym przypadku frakcja jest podzielna przez x 1 .
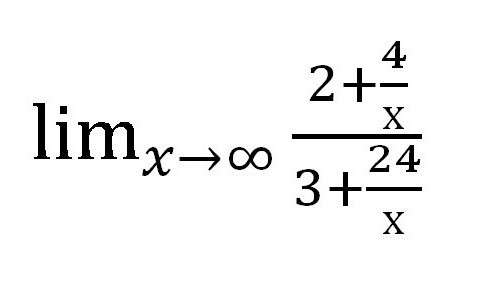
Następnie dowiemy się, jaką wartość ma każdy dodatek zawierający zmienną. W tym przypadku ułamek. Jako x → ∞ wartość każdej z frakcji ma tendencję do zera. Wykonując pracę pisemną, warto przytoczyć takie przypisy:
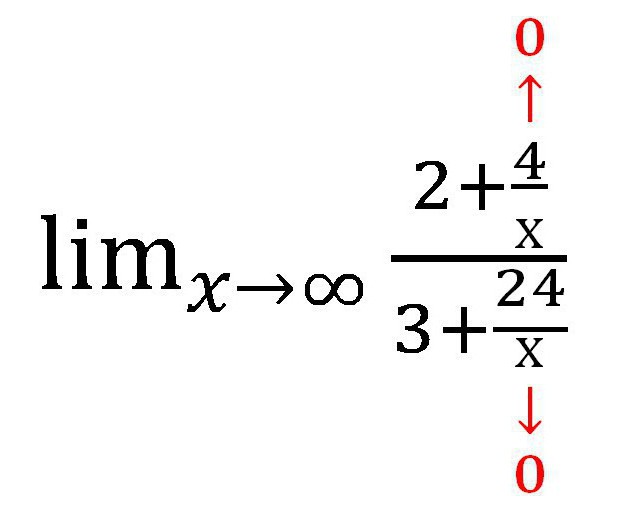
Otrzymano następujące wyrażenie:
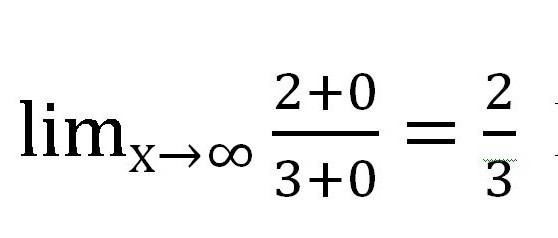
Oczywiście, frakcje zawierające x nie stały się zerami! Ale ich wartość jest tak mała, że nie można jej wziąć pod uwagę przy obliczaniu. W rzeczywistości, x nigdy nie będzie równe 0 w tym przypadku, ponieważ zero nie może być podzielone.
Czym jest sąsiedztwo?
Przypuśćmy, że profesor ma do dyspozycji złożoną sekwencję, oczywiście podaną nie mniej złożoną formułą. Profesor znalazł odpowiedź, ale czy jest odpowiedni? W końcu wszyscy ludzie się mylą.
Auguste Cauchy w swoim czasie wymyślił świetny sposób na udowodnienie granic sekwencji. Jego metoda nazywała się operowaniem sąsiedztwa.
Załóżmy, że istnieje jakiś punkt a, jego sąsiedztwo w obu kierunkach na linii liczbowej to ε ("epsilon"). Ponieważ ostatnia zmienna to odległość, jej wartość jest zawsze dodatnia.
Teraz definiujemy pewną sekwencję x n i przyjmujemy, że dziesiąty termin sekwencji (x 10 ) wchodzi w okolicę a. Jak napisać ten fakt w języku matematycznym?
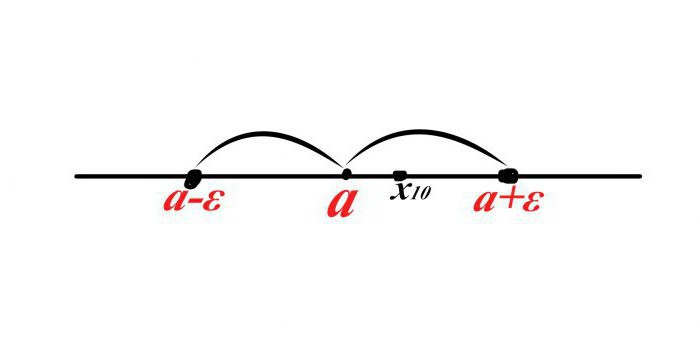
Załóżmy, że x 10 znajduje się na prawo od punktu a, wtedy odległość wynosi x 10 -a <ε, jednak jeśli umieścisz "X dziesiąty" na lewo od punktu a, wtedy odległość będzie ujemna, ale jest to niemożliwe, wtedy powinieneś dodać lewą część nierówności do modułu. Otrzymujemy | x 10-a | <ε.
Teraz nadszedł czas, aby w praktyce wyjaśnić tę formułę, o której wspomniano powyżej. Pewna liczba a jest słusznie nazywana punktem końcowym sekwencji, jeśli dla którejkolwiek z jej granic jest spełniona nierówność ε> 0, a całe sąsiedztwo ma swoją własną naturalną liczbę N, tak, że wszystkie elementy sekwencji o bardziej znaczących liczbach będą wewnątrz sekwencji | x n - a | <ε .
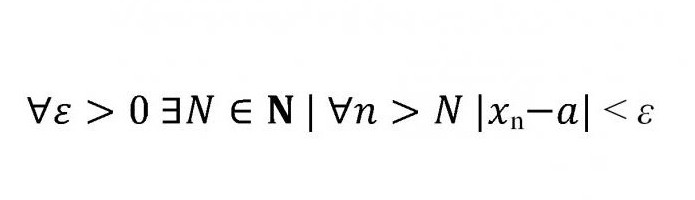
Przy takiej wiedzy łatwo jest wdrożyć rozwiązanie do granic sekwencji, aby udowodnić lub obalić gotową odpowiedź.
Twierdzenia
Twierdzenia o ograniczeniach sekwencji są ważnym składnikiem teorii, bez której praktyka nie jest możliwa. Istnieją tylko cztery główne twierdzenia, pamiętając o tym, że czasami możliwe jest ułatwienie przebiegu rozwiązania lub dowodu:
- Unikalność ograniczenia sekwencji. Limit dla dowolnej sekwencji może wynosić tylko jeden lub wcale. Ten sam przykład z kolejką, która może mieć tylko jeden koniec.
- Jeśli seria liczb ma limit, sekwencja tych liczb jest ograniczona.
- Limit sumy (różnicy, iloczynu) sekwencji jest równy sumie (różnicy, produktu) ich granic.
- Granica ilorazu z podziału dwóch ciągów jest równa ilorazowi granic wtedy i tylko wtedy, gdy mianownik nie zniknie.
Dowód sekwencji
Czasami konieczne jest rozwiązanie problemu odwrotnego, aby udowodnić określony limit sekwencji liczbowej. Rozważ przykład.
Wykazać, że granica sekwencji podana przez formułę wynosi zero.
Zgodnie z zasadą omówioną powyżej, dla dowolnej sekwencji musi być spełniona nierówność | x n - a | <ε. Zastąp określoną wartość i punkt odniesienia. Otrzymujemy:
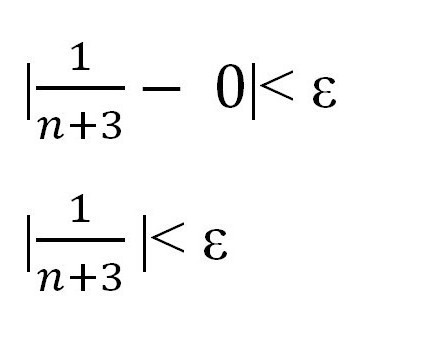
Wyraź n za pomocą "epsilon", aby pokazać istnienie pewnej liczby i udowodnić istnienie sekwencji granicznej.
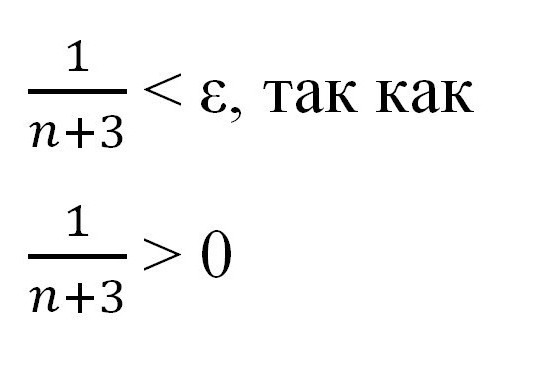
Na tym etapie ważne jest, aby pamiętać, że "epsilon" i "en" są liczbami dodatnimi i niezerowymi. Teraz możesz kontynuować dalsze transformacje, korzystając z wiedzy o nierównościach uzyskanych w szkole średniej.
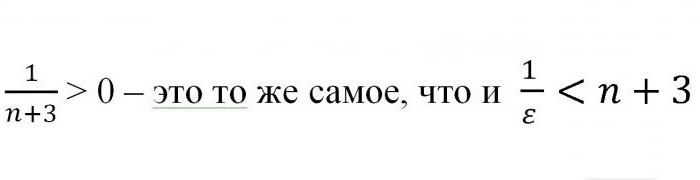
Stąd okazuje się, że n> -3 + 1 / ε. Ponieważ warto pamiętać, że mówimy o liczbach naturalnych, wynik można zaokrąglić, umieszczając w nawiasach kwadratowych. W ten sposób udowodniono, że dla każdej wartości sąsiedztwa "epsilon" punktu a = 0 istniała wartość taka, że początkowa nierówność utrzymuje się. Z tego możemy śmiało powiedzieć, że liczba a jest limitem danej sekwencji. Co trzeba było udowodnić.
Przy tak wygodnej metodzie można udowodnić granicę sekwencji liczbowej, jednak na pierwszy rzut oka może się to wydawać skomplikowane. Najważniejsze - nie panikuj na widok pracy.
A może nie jest?
Istnienie sekwencji granicznej jest w praktyce opcjonalne. Możesz łatwo znaleźć taką serię liczb, które naprawdę nie mają końca. Na przykład ten sam flasher x n = (-1) n . jest oczywiste, że sekwencja składająca się tylko z dwóch liczb, cyklicznie powtarzających się, nie może mieć granicy.
Ta sama historia jest powtarzana z sekwencjami składającymi się z jednej liczby, ułamkowej, mającej w trakcie obliczeń niepewność dowolnej kolejności (0/0, ∞ / ∞, ∞ / 0 itd.). Należy jednak pamiętać, że ma również miejsce błędne obliczenie. Czasami ograniczenie sekwencji pomoże ponownie sprawdzić własne rozwiązania.
Sekwencja monotoniczna
Powyżej rozważaliśmy kilka przykładów sekwencji, metod ich rozwiązywania, a teraz spróbujemy przyjąć bardziej konkretny przypadek i nazwać go "sekwencją monotoniczną".
Definicja: rzetelne jest wywoływanie dowolnej sekwencji monotonnie rosnącej, jeśli zachowana jest dla niej surowa nierówność x n <x n +1. Również każda sekwencja jest słusznie zwana monotonną malejącą, jeśli nierówność x n > x n +1 dla niej zachodzi .
Wraz z tymi dwoma warunkami istnieją również podobne słabe nierówności. Odpowiednio, x n ≤ x n +1 (nie malejąca sekwencja) i x n ≥ x n +1 (sekwencja nie rosnąca).
Ale łatwiej jest to zrozumieć na przykładach.
Sekwencja podana za pomocą wzoru x n = 2 + n tworzy następującą serię liczb: 4, 5, 6 itd. Jest to monotonicznie rosnąca sekwencja.
A jeśli weźmiemy x n = 1 / n, otrzymamy serię: 1/3, ¼, 1/5 itd. Jest to sekwencja monotonicznie malejąca.
Granica zbieżnej i ograniczonej sekwencji
Ograniczona sekwencja - sekwencja z ograniczeniem. Sekwencja zbieżna to seria liczb, która ma nieskończenie mały limit.
Zatem granica sekwencji ograniczonej jest dowolna ważna lub liczba zespolona. Pamiętaj, że może istnieć tylko jeden limit.
Granica sekwencji zbieżnej jest nieskończenie małą (rzeczywistą lub złożoną). Jeśli narysujesz diagram sekwencji, to w pewnym momencie zdaje się zbiegać, aby dążyć do przejścia do określonej wartości. Stąd nazwa - sekwencja zbieżna.
Monotonny limit
Limit takiej sekwencji może być lub może nie być. Na początku przydatne jest zrozumienie, kiedy jest, od którego można odepchnąć, gdy udowadnia brak limitu.
Wśród monotonna sekwencje emitują zbieżne i rozbieżne. Zbieżność jest sekwencją utworzoną przez zbiór x i ma rzeczywisty lub złożony limit w zbiorze. Rozbieżność - sekwencja, która nie ma limitu w swoim zbiorze (ani rzeczywistym, ani złożonym).
Co więcej, sekwencja zbiega się, jeśli jej obraz geometryczny zbiega się z górnymi i dolnymi granicami.
Granica sekwencji zbieżnej w wielu przypadkach może być równa zeru, ponieważ każda nieskończenie mała sekwencja ma znaną granicę (zero).
Niezależnie od sekwencji zbieżności, wszystkie są ograniczone, ale nie wszystkie ograniczone sekwencje zbiegają się.
Suma, różnica, iloczyn dwóch zbieżnych sekwencji jest również sekwencją zbieżną. Jednak iloraz może być również zbieżny, jeśli jest zdefiniowany!
Różne akcje z ograniczeniami
Granice sekwencji są tak samo znaczące (w większości przypadków), jak liczby i liczby: 1, 2, 15, 24, 362 itd. Okazuje się, że niektóre operacje mogą być wykonywane z ograniczeniami.
Po pierwsze, podobnie jak liczby i liczby, limity dowolnych sekwencji można dodawać i odejmować. Na podstawie trzeciego twierdzenia o granicach ciągów zachowuje się następująca równość: granica sumy sekwencji równa się sumie ich granic.
Po drugie, w oparciu o czwarte twierdzenie o granicach sekwencji, prawdziwa jest następująca równość: granica iloczynu n-tej liczby sekwencji jest równa iloczynowi ich granic. To samo odnosi się do podziału: granica ilorazu dwóch sekwencji jest równa ilorazowi ich granic, pod warunkiem, że limit nie wynosi zero. W końcu, jeśli granica ciągów równa się zero, otrzymamy dzielenie przez zero, co jest niemożliwe.
Właściwości sekwencji
Wydaje się, że limit sekwencji liczbowej został już szczegółowo przeanalizowany, ale takie wyrażenia, jak "nieskończenie małe" i "nieskończenie duże", są wymieniane więcej niż raz. Oczywiście, jeśli istnieje sekwencja 1 / x, gdzie x → ∞, to taka frakcja jest nieskończenie mała, a jeśli ta sama sekwencja, ale granica dąży do zera (x → 0), to frakcja staje się nieskończenie dużą wielkością. I takie ilości mają swoje własne cechy. Właściwości limitu sekwencji o dowolnych małych lub dużych wartościach są następujące:
- Suma dowolnej ilości arbitralnie małych ilości będzie również niewielką ilością.
- Suma dowolnej liczby dużych ilości będzie nieskończenie dużą ilością.
- Iloczyn arbitralnie małych ilości jest nieskończenie mały.
- Iloczyn dużej liczby jest nieskończenie dużą wartością.
- Jeśli oryginalna sekwencja zmierza do nieskończenie dużej liczby, to wielkość przeciwległa do niej będzie nieskończenie mała i będzie miała tendencję do zera.
W rzeczywistości obliczanie granicy sekwencji nie jest tak trudnym zadaniem, jeśli znasz prosty algorytm. Ale granice sekwencji - temat wymagający maksymalnej uwagi i wytrwałości. Oczywiście wystarczy po prostu uchwycić istotę rozwiązania takich wyrażeń. Zaczynając od małych, z czasem osiągasz duże szczyty.