Jak przeprowadzić pełne badanie funkcji

W tym artykule przyjrzymy się schematowi badania funkcji, a także podamy przykłady badań ekstremalnych, monotonicznych i asymptotycznych tej funkcji.

Schemat

1. Funkcja obszaru istnienia (DHS).
2. Przecięcie funkcji (jeśli występuje) z osiami współrzędnych, znakami funkcji, parzystością, okresowością.
3. Punkty przerwania (ich rodzaj). Ciągłość. Pionowe asymptoty.
4. Monotonia i punkty ekstremalne.
5. Punkty przegięcia Bulge
6. Badanie funkcji w nieskończoności, na asymptotach: poziomych i ukośnych.
7. Wykreślanie.

Studium monotonii

Twierdzenie. Jeżeli funkcja g jest ciągła na [a, b] , różnicowana przez (a; b) i g '(x) ≥ 0 (g' (x) ≤0) , xє (a; b) , to g rośnie (maleje) o [a, b] .

Przykład:

y = 1: 3x ³ - 6: 2x ² + 5x.

DHS: xR

y '= x ² + 6x + 5.

Znajdź interwały stałych znaków y ' . Ponieważ y ' jest funkcją elementarną, może zmieniać znaki tylko w punktach, w których zmienia się w zero lub nie istnieje. Jej DHS: xR .

Znajdź punkty, których pochodna wynosi 0 (zero):

y '= 0;

x = -1; -5.

Więc rośnie na (-∞; -5) i na [-1; + ∞), y zstępujące do [1; 2] .

Ekstremalne badanie

T. x ₀ nazywany _jest punktem maksymalnym (maks.) Na zbiorze A funkcji g, gdy jako funkcję w tym punkcie przyjmuje się wartość g (x ₀ ) ≥ g (x), xєA .

T. x ₀ nazywany _jest minimalnym punktem (min) funkcji g na zbiorze A, gdy najmniejszy g (x ₀ ) ≤ g (x), xєA jest przyjmowany jako funkcja w tym punkcie .

Na zbiorze A maksymalne punkty (maksimum) i minimum (min) są nazywane punktami ekstremum g . Takie ekstremy są również nazywane absolutnymi skrajnościami na planie .

Jeśli x ₀ jest ekstremalnym punktem g w pewnej dzielnicy, to x ₀ jest nazywane punktem lokalnego lub lokalnego ekstremum (max lub min) g.

Twierdzenie (wymagany warunek). Jeśli x ₀ jest punktem ekstremalnym funkcji (lokalnej) g , to pochodna nie istnieje lub jest równa w tym r. 0 (zero).

Definicja Punktami krytycznymi są punkty z nieistniejącą lub równą 0 (zero) pochodną. Te punkty danych są podejrzane w ekstremum.

Twierdzenie (warunek nr 1). Jeśli funkcja g jest ciągła w pewnym sąsiedztwie t. X _0, a znak zmienia swoją pochodną na przejściu, wówczas dany punkt ma skrajność g .

Twierdzenie (warunek nr 2). Niech funkcja w pewnej dzielnicy będzie różniczkowalna dwukrotnie, a g '= 0, g> 0 (g <0) , a następnie ten punkt jest punktem funkcji maksymalnej (max) lub minimalnej (min).

Badanie Bulge

Funkcja nazywana jest wypukłym w dół (lub wklęsłym) w przedziale (a, b), gdy wykres funkcji nie jest wyższy od siecznego w przedziale dla dowolnego x z (a, b), który przechodzi przez te punkty .

Funkcja będzie wypukła wyłącznie w dół (a, b) , jeśli - wykres znajduje się poniżej siecznego na luce.

Funkcja nazywana jest wypukłym do góry (wypukłym) w przedziale (a, b) , jeśli dla dowolnych punktów t с (a, b) wykres funkcji w przedziale nie jest niższy niż sędzia przechodzący przez absyle w tych punktach .

Funkcja będzie ściśle wypukła w górę na (a, b ), jeśli - wykres na przedziale leży nad siecznym.

Jeśli funkcja w dzielnicy jest punktem jest ciągła, a po t. x ₀ funkcja zmienia wypukłość na przejściu, ten punkt nazywamy punktem przegięcia funkcji.

Test asymptotyczny

Definicja Prosta jest nazywana asymptotią g (x), jeśli w nieskończonej odległości od początku współrzędnych zbliża się punkt wykresu funkcji: d (M, l).

Asymptoty mogą być pionowe, poziome i ukośne.

Pionowa linia z równaniem x = x ₀ będzie asymptotą pionowego wykresu funkcji g jeśli w t. x _{0 jest} nieskończoną luką, to znaczy co najmniej jedna lewa lub prawa granica w tym punkcie to nieskończoność.

Badanie funkcji w segmencie na wartość najmniejszego i największego

Jeśli funkcja jest ciągła w [a, b] , to zgodnie z twierdzeniem Weierstrassa jest największa wartość i najmniejsza wartość w tym segmencie, to znaczy są t punkty należące do [a, b] takie, że g (x ₁ ) ≤ g (x) <g (x ₂ ), x ₂ є [a, b]. Na podstawie twierdzeń o monotoniczności i ekstremie otrzymujemy następujący schemat do badania funkcji w segmencie dla najmniejszej i największej wartości.

Planuj

1. Znajdź pochodną g '(x) .
2. Znajdź wartość funkcji g w tych punktach i na końcach segmentu.
3. Znalezione wartości porównać i wybrać najmniejszy i największy.

Uwaga Jeśli chcesz badać funkcję na skończonym przedziale (a, b) lub na nieskończonym (-∞; b); (-∞; + ∞) na wartości maksymalnej i minimalnej, a następnie w planie, zamiast wartości funkcji na końcach luki, przeszukiwane są odpowiednie jednostronne granice: zamiast f (a), zamiast f (b), f (a +) = szukana jest część (x). (-b) Możesz więc znaleźć funkcje LDU w tym przedziale, ponieważ absolutne ekstremum niekoniecznie istnieją w tym przypadku.

Zastosowanie pochodnej do rozwiązania problemów aplikacyjnych na ekstremum pewnych wielkości

1. Wyrażaj tę wartość w kategoriach innych wartości od stanu problemu, tak aby była to funkcja tylko jednej zmiennej (jeśli to możliwe).
2. Określić okres zmiany tej zmiennej.
3. Przeprowadź badanie funkcji w przedziale przy wartościach maksymalnych i minimalnych.

Zadanie. Konieczne jest zbudowanie prostokątnej platformy, przy użyciu mierników sieci, przy ścianie tak, aby z jednej strony pasowało do ściany, a na pozostałych trzech jest ogrodzone siatką. Przy jakim współczynniku proporcji obszar takiej strony będzie największy?

S = xy jest funkcją dwóch zmiennych.

S = x (a - 2x) - funkcja pierwszej zmiennej ; x є [0; a: 2].

S = ax - 2x ² ; S '= a - 4x = 0, xєR, x = a: 4.

S (a: 4) = a ² : 8 to najwyższa wartość;

S (0) = 0.

Znajdź drugą stronę prostokąta: = a: 2.

Współczynnik proporcji: y: x = 2.

Odpowiedź jest. Największa powierzchnia będzie równa 2/8 , jeśli strona równoległa do ściany jest 2 razy większa niż druga strona.

Funkcja badawcza. Przykłady

Przykład 1

Istnieje y = x ³ : (1-x) ² . Wykonaj badania.

1. DHS: xє (-∞; 1) U (1; ∞).
2. Ogólna postać funkcji (ani parzysta, ani nieparzysta) nie jest symetryczna względem punktu 0 (zero).
3. Znaki funkcji. Funkcja jest elementarna, więc może zmienić znak tylko w punktach, w których jest 0 (zero) lub nie istnieje.
4. Funkcja jest elementarna, dlatego ciągła na DHS: (-∞; 1) U (1; ∞).

Luka: x = 1;

limx ³ : (1- x) ² = ∞ - Nieciągłość drugiego rodzaju (nieskończoność), więc w punkcie 1 znajduje się pionowa asymptota;

x = 1 to równanie pionowej asymptoty.

5. y '= x ² (3 - x): (1 - x) ³ ;

DHS (y '): x ≠ 1;

x = 1 - punkt krytyczny.

y '= 0;

0; 3 - punkty krytyczne.

6. y "= 6x: (1 - x) ⁴ ;

Krytyczny t .: 1, 0;

x = 0 - m. załamania, y (0) = 0.

7. limx ³ : (1 - 2x + x ² ) = ∞ - nie ma poziomej asymptoty, ale może być nachylona.

k = 1 to liczba;

b = 2 to liczba.

Dlatego istnieje asymptota nachylona y = x + 2 przy + ∞ i at - ∞.

Przykład 2

Biorąc pod uwagę y = (x ² + 1): (x - 1). Aby tworzyć i badać. Zbuduj wykres.

1. Dziedziną istnienia jest cała linia liczbowa, za wyjątkiem m. X = 1 .

2. y przecina OY (jeśli to możliwe) wm. (0; g (0)) . Znajdź y (0) = -1 - t. przecięcie OY .

Znaleźliśmy punkty przecięcia wykresu z OX, rozwiązując równanie y = 0 . Równanie podstawowe nie ma poprawnego, dlatego ta funkcja nie przecina się z OX .

3. Funkcja nie jest okresowa. Rozważ wyrażenie

g (-x) ≠ g (x) i g (-x) -g (x) . Oznacza to, że jest to funkcja ogólna (ani parzysta, ani nieparzysta).

4. T. x = 1 luka ma drugi rodzaj. We wszystkich innych punktach funkcja jest ciągła.

5 Funkcja badania na ekstremum:

(x ² - 2x - 1): (x - 1) ² = y '

i rozwiąż równanie y '= 0.

Tak więc 1 - √2, 1 + √2, 1 - punkty krytyczne lub punkty możliwej ekstremum. Punkty te dzielą linię numeryczną na cztery interwały .

W każdym przedziale pochodna ma określony znak, który można ustawić za pomocą metody interwałów lub poprzez obliczenie wartości pochodnej w poszczególnych punktach. W odstępach (-∞; 1 - √2 ) U ( 1 + √2 ; ∞) pochodna dodatnia oznacza, że ​​funkcja rośnie; jeśli xє ( 1 - √2 ; 1) U (1; 1 + √2 ) , funkcja maleje, ponieważ w tych przedziałach pochodna jest ujemna. Przez t. X _1, gdy idziesz (przesuwając się od lewej do prawej), zmienia znak wyprowadzony z "+" na "-", dlatego w tym momencie istnieje lokalne maksimum, które znajdujemy

y _max = 2 - 2 √2 .

Podczas przechodzenia przez x ₂ zmienia znak wyprowadzony z "-" na "+", w związku z tym w tym momencie istnieje lokalne minimum, i

y _mix = 2 + 2√2.

T. x = 1 nie jest tak ekstremum.

6. 4: (x - 1) ³ = y ".

Przy (-∞; 1 ) 0> y " , w konsekwencji, w tym przedziale krzywa jest wypukła; jeśli xє ( 1 ; ∞) - krzywa jest wklęsła. W t punkt 1 funkcja nie jest zdefiniowana, dlatego punkt ten nie jest punktem przegięcia.

7 Z wyników pkt 4 wynika, że x = 1 jest asymptotyczną krzywą pionową.

Asymptoty poziome są nieobecne.

x + 1 = y to asymptota nachylona przez tę krzywą. Nie ma innych asymptot.

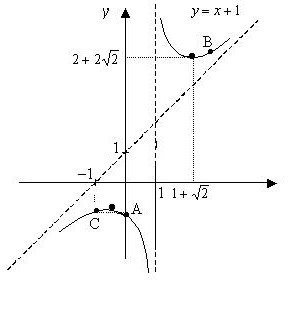
8. Biorąc pod uwagę przeprowadzone badania, tworzymy wykres (patrz rysunek powyżej).