Jak znaleźć obszar wielokąta?

W przypadku problemów z geometrią często wymagane jest obliczenie obszaru wielokąta. Co więcej, może mieć dość zróżnicowany kształt - od znanego trójkąta do pewnego n-gona z pewną niewyobrażalną liczbą wierzchołków. Ponadto te wielokąty są wypukłe lub wklęsłe. W każdej sytuacji ma opierać się na wyglądzie postaci. Okazuje się więc, że najlepiej wybrać rozwiązanie problemu. Kształt może być poprawny, co znacznie uprości rozwiązanie problemu.

Trochę teorii wieloboku

Jeśli zostaną narysowane trzy lub więcej przecinających się linii prostych, tworzą one pewną liczbę. To jest wielobok. Przez liczbę punktów przecięcia staje się jasne, ile będzie mieć wierzchołków. Podają nazwę wynikowej liczby. Może to być:

• trójkąt;
• czworoboczny;
• penta lub sześciokąt i tak dalej.

Taka liczba będzie na pewno charakteryzować się dwoma przepisami:

1. Sąsiednie boki nie należą do jednej linii prostej.
2. Punkty niesąsiadujące nie mają wspólnych punktów, tzn. Nie przecinają się.

Aby zrozumieć, które wierzchołki są sąsiadujące, musisz sprawdzić, czy należą one do tej samej strony. Jeśli tak, to następny. W przeciwnym razie mogą być połączone segmentem, który należy nazwać przekątną. Mogą być rysowane tylko w wielokątach, które mają więcej niż trzy wierzchołki.

Jakie są ich typy?

Wielokąt o więcej niż czterech rogach może być wypukły lub wklęsły. Różnica tych ostatnich polega na tym, że niektóre z jego wierzchołków mogą leżeć po przeciwnych stronach linii prostej biegnącej przez dowolną stronę wieloboku. W wypukłym, wszystkie wierzchołki zawsze leżą po jednej stronie takiej linii.

W szkolnym kursie geometrii przez większość czasu podaje się dokładnie wypukłe figury. Dlatego w problemach należy znaleźć obszar wypukłego wielokąta. Następnie istnieje formuła poprzez promień ograniczonego okręgu, która pozwala znaleźć pożądaną wartość dla dowolnego kształtu. W innych przypadkach nie istnieje unikalne rozwiązanie. W przypadku trójkąta wzór jest jeden, a dla kwadratu lub trapezu zupełnie inny. W sytuacjach, w których liczba jest błędna lub jest wiele szczytów, zwyczajowo dzieli się je na proste i znajome.

Co zrobić, jeśli element ma trzy lub cztery wierzchołki?

W pierwszym przypadku będzie to trójkąt i możesz użyć jednej z następujących formuł:

• S = 1/2 * a * n, gdzie a jest bokiem, n jest wysokością do niego;
• S = 1/2 * a * b * sin (A), gdzie a i b są bokami trójkąta, A jest kątem między znanymi bokami;
• S = √ (p * (p - a) * (p - c) * (p - c)), gdzie c jest bokiem trójkąta, do już zaznaczonych dwóch, p jest półobrzegiem, czyli sumą wszystkich trzech boków, podzielonych na dwa .

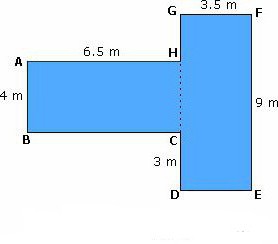
Figura z czterema wierzchołkami może być równoległobokiem:

• S = a * n;
• S = 1/2 * d ₁ * d ₂ * sin (α), gdzie d ₁ i d ₂ są przekątnymi, α ​​jest kątem między nimi;
• S = a * in * sin (α).

Formuła dla obszary trapezowe: S = n * (a + b) / 2, gdzie aib oznaczają długości zasad.

Co zrobić ze zwykłym wielokątem z więcej niż czterema wierzchołkami?

Na początek taka postać charakteryzuje się tym, że w niej wszystkie strony są równe. Ponadto wielokąt ma te same kąty.

Jeśli koło wokół takiej figury zostanie opisane, wówczas jego promień będzie się pokrywał z segmentem od środka wielokąta do jednego z wierzchołków. Dlatego, aby obliczyć obszar zwykłego wielokąta z dowolną liczbą wierzchołków, potrzebujemy następującej formuły:

S _n = 1/2 * n * R _n ² * sin (360º / n), gdzie n jest liczbą wierzchołków wielokąta.

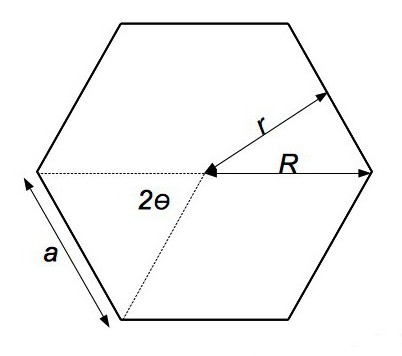
Z tego łatwo jest uzyskać taki, który jest przydatny w szczególnych przypadkach:

1. trójkąty: S = (3√3) / 4 * R ² ;
2. kwadrat: S = 2 * R ² ;
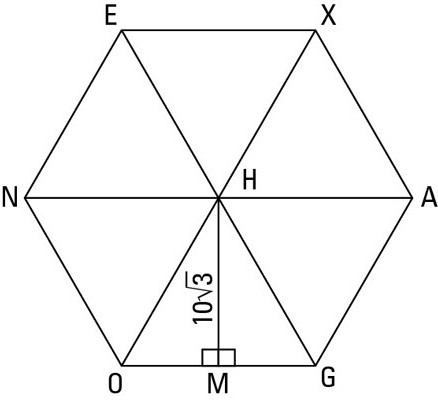
3. sześciokąt: S = (3√3) / 2 * R ² .

Sytuacja z nieprawidłową liczbą

Sposób, w jaki można znaleźć obszar wielokąta, jeśli nie jest prawidłowy i nie można go przypisać do żadnej z wcześniej znanych liczb, to algorytm:

• podziel go na proste kształty, takie jak trójkąty, aby się nie przecinały;
• obliczyć ich powierzchnię za pomocą dowolnej formuły;
• dodać wszystkie wyniki.

Co zrobić, jeśli w problemie podane są współrzędne wierzchołków wielokąta?

Oznacza to, że znany jest zestaw par liczb dla każdego punktu, które ograniczają boki figury. Zwykle są one zapisywane jako (x ₁ ; y ₁ ) dla pierwszego, (x ₂ ; y ₂ ) dla drugiego, a n-ty wierzchołek ma te wartości (x _n ; y _n ). Następnie obszar wieloboku definiuje się jako sumę n terminów. Każdy z nich wygląda następująco: ((y _{i + 1} + y _i ) / 2) * (x _{i + 1} - x _i ). W tym wyrażeniu i zmienia się od jednego do n.

Należy zauważyć, że znak wyniku będzie zależał od obejścia kształtu. Podczas używania określonej formuły i poruszania się zgodnie z ruchem wskazówek zegara odpowiedź będzie negatywna.

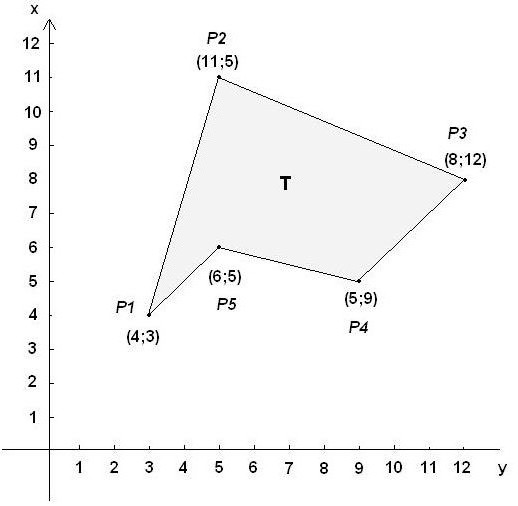
Przykładowe zadanie

Stan Współrzędne wierzchołków są określone wartościami (0,6, 2,1), (1,8; 3,6), (2,2; 2,3), (3,6; 2,4), (3,1; 0,5). Wymagany do obliczenia obszaru wielokąta.

Decyzja. Zgodnie ze wzorem powyżej, pierwszy termin będzie (1,8 + 0,6) / 2 * (3,6 - 2,1). Tutaj wystarczy wziąć wartości dla gry i X z drugiego i pierwszego punktu. Prosta kalkulacja doprowadzi do wyniku 1.8.

Drugi termin jest podobnie uzyskany: (2,2 + 1,8) / 2 * (2,3 - 3,6) = -2,6. Przy rozwiązywaniu takich problemów nie bój się wartości ujemnych. Wszystko idzie tak, jak powinno. To jest zaplanowane.

Podobnie, wartości uzyskuje się dla trzeciego (0,29), czwartego (-6,36) i piątego terminu (2,96). Łączna powierzchnia wynosi: 1,8 + (-2,6) + 0,29 + (-6,36) + 2,96 = - 3,915.

Rada do rozwiązania problemu, dla którego wielobok jest przedstawiony na papierze w komórce

Najczęściej zastanawiające jest to, że w danych znajduje się tylko rozmiar komórki. Okazuje się jednak, że więcej informacji nie jest potrzebnych. Zaleceniem rozwiązania tego problemu jest podzielenie kształtu na wiele trójkątów i prostokątów. Ich obszar jest dość prosty, aby policzyć długość stron, które następnie można łatwo spasować.

Ale często istnieje prostsze podejście. Polega na narysowaniu figury do prostokąta i obliczeniu wartości jego powierzchni. Następnie policz obszary tych elementów, które były zbędne. Odejmij je od całości. Ta opcja czasami wymaga nieco mniejszej liczby akcji.