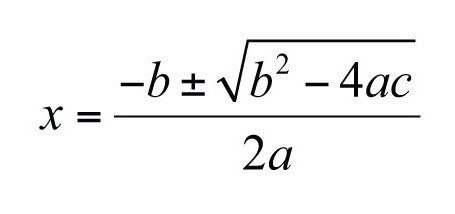Jak znaleźć pierwiastek równania: liniowy, kwadratowy, sześcienny?
Równania matematyczne są tak samo ważne jak czasowniki w języku rosyjskim. Bez możliwości znalezienia korzenia równania trudno jest twierdzić, że student opanował kurs algebry. Ponadto dla każdego gatunku istnieją własne, specyficzne rozwiązania.
Co to jest?
Równanie to dwa dowolne wyrażenia zawierające zmienne z równym znakiem między nimi. Co więcej, liczba nieznanych wielkości może być dowolna. Minimalna liczba to jedna.
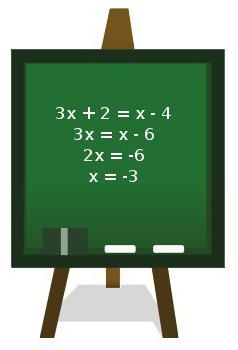
Aby go rozwiązać, należy sprawdzić, czy istnieje korzeń równania. Jest to liczba, która zamienia ją w prawidłową równość. Jeśli nie, odpowiedź brzmi: "nie ma korzeni". Ale może być odwrotnie, gdy odpowiedź jest mnogością liczb.
Jakie rodzaje równań istnieją?
Liniowy. Zawiera zmienną, której stopień jest równy jeden.
- Kwadrat. Zmienna ma moc 2, a transformacja w takim stopniu.
- Równanie najwyższego stopnia.
- Ułamkowe racjonalne. Gdy zmienna jest w mianowniku ułamka.
- Z modułem.
- Irracjonalny Oznacza to, że zawiera algebraiczny katalog główny.
W jaki sposób rozwiązano równanie liniowe?
To jest główny. Do tego poglądu wszyscy inni dążą do przewodzenia. Ponieważ łatwo jest znaleźć pierwiastek równania.
- Najpierw należy wykonać możliwe transformacje, czyli rozwinąć nawiasy i podać podobne warunki.
- Przesuń wszystkie monomiki zmienną po lewej stronie równania, pozostawiając wolne terminy po prawej stronie.
- Przynieś podobne terminy w każdej części równania, które ma zostać rozwiązane.
- W wynikowej równości w jego lewej połowie będzie iloczyn współczynnika i zmiennej, aw prawej połowie liczby.
- Pozostaje znaleźć pierwiastek równania, dzieląc liczbę po prawej, przez współczynnik przed nieznanym.
Jak znaleźć korzenie równania kwadratowego?
Po pierwsze, należy zredukować do standardowej formy, to znaczy, wszystkie nawiasy powinny zostać otwarte, należy wprowadzić podobne terminy, a wszystkie monomiały powinny zostać przesunięte na lewą stronę. Po prawej stronie równości powinno pozostać tylko zero.
- Użyj formuły dyskryminacyjnej. Skracając współczynnik przed nieznanym o stopień "1". Pomnożyć wolny monomialny i liczbę przed zmienną w kwadracie z liczbą 4. Odejmij produkt od wynikowego kwadratu.
- Oszacuj wartość dyskryminatora. Jest negatywny - decyzja jest skończona, ponieważ nie ma korzeni. Równy zero - odpowiedź to jedna liczba. Dodatnie - dwie wartości zmiennej.
Znajdź dwa pierwiastki równania według formuły, w której pierwiastek kwadratowy od dyskryminatora należy odjąć lub dodać do ujemnego współczynnika zmiennej w pierwszym stopniu. Następnie podziel przez podwójny współczynnik od strony placu nieznanego. (W przypadku równości dyskryminatora, zero będzie musiało być dodane lub odjęte, więc dwa korzenie będą się pokrywać.)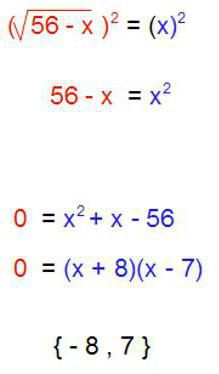
Jak rozwiązać równanie sześcienne?
Najpierw znajdź pierwiastek równania x. Określa się ją za pomocą metody selekcji z liczb, które są dzielnikami wolnego terminu. Ta metoda jest dogodna do rozważenia konkretnego przykładu. Niech równanie będzie: x 3 - 3x 2 - 4x + 12 = 0.
Jego wolny termin wynosi 12. Następnie dzielniki, które muszą zostać sprawdzone, będą liczbami dodatnimi i ujemnymi: 1, 2, 3, 4, 6 i 12. Wyszukiwanie może być zakończone na numerze 2. Daje prawdziwą równość w równaniu. Oznacza to, że jego lewa strona okazuje się być zerowa. Więc numer 2 jest pierwszy sześcienny korzeń równania.
Teraz musisz podzielić pierwotne równanie przez różnicę między zmienną a pierwszym rootem. W konkretnym przykładzie jest to (x - 2). Prosta transformacja prowadzi licznik do takiej faktoryzacji: (x - 2) (x + 2) (x - 3). Te same czynniki licznika i mianownika są zredukowane, a pozostałe dwa nawiasy w ujawnieniu dają proste równanie kwadratowe: x 2 - x - 6 = 0.
Tutaj znajdź dwa pierwiastki równania zgodnie z zasadą opisaną w poprzedniej sekcji. Są to liczby: 3 i -2.
Zatem konkretne równanie sześcienne ma trzy pierwiastki: 2, -2 i 3.
W jaki sposób rozwiązuje się systemy równania liniowe?
Tutaj proponuje się metodę eliminowania niewiadomych. Polega na wyrażeniu jednej osoby nieznanej przez drugą w jednym równaniu i zastąpieniu tego wyrażenia innym. Ponadto, rozwiązanie układu dwóch równań z dwoma niewiadomymi jest zawsze parą zmiennych.
Jeśli zmienne w nich są oznaczone literami x 1 i x 2 , możemy wyprowadzić z pierwszego równania, na przykład x 2 . Następnie jest podstawiony do drugiego. Przeprowadzana jest niezbędna transformacja: ujawnienie nawiasów i przymus podobnych członków. Okazuje się, że proste równanie liniowe, którego korzeń jest łatwy do obliczenia.
Teraz wróć do pierwszego równania i znajdź pierwiastek równania x 2 , używając wynikowego równania. Te dwie liczby są odpowiedzią.
Prosta rada
Aby mieć pewność co do otrzymanej odpowiedzi, zaleca się zawsze sprawdzenie. Nie trzeba pisać.
Jeśli jedno równanie zostanie rozwiązane, to każdy z jego pierwiastków musi zostać zastąpiony pierwotną równością i uzyskać te same liczby w obu jego częściach. Wszystko razem - właściwa decyzja.
Podczas pracy z systemem konieczne jest zastąpienie korzeni w każdym rozwiązaniu i wykonanie wszystkich możliwych działań. Okazuje się, że poprawna równość? Decyzja jest prawidłowa.