Energia kinetyczna - energia ruchu ciał
Potencjał i energia kinetyczna pozwalają nam scharakteryzować stan każdego ciała. Jeśli ten pierwszy jest używany w systemach oddziałujących obiektów, to drugi jest związany z ich ruchem. Te rodzaje energii są z reguły brane pod uwagę, gdy siła łącząca ciała jest niezależna od trajektorii ruchu. W takim przypadku ważne są tylko pozycje początkowe i końcowe.
Ogólne informacje i koncepcje
Energia kinetyczna układu jest jedną z jego najważniejszych cech. Fizycy rozróżniają dwa rodzaje takiej energii w zależności od rodzaju ruchu:
• progresywny;
• obrót.
Energia kinetyczna (E k ) jest różnicą między całkowitą energią układu a resztą energii. Na tej podstawie możemy powiedzieć, że jest to spowodowane ruchem systemu. Ciało ma to tylko wtedy, gdy się porusza. W spoczynku obiekt wynosi zero. Energia kinetyczna ciał zależy wyłącznie od prędkości ruchu i ich mas. Całkowita energia systemu jest bezpośrednio zależna od prędkości jego obiektów i odległości między nimi.
Podstawowe formuły
W przypadku, gdy jakakolwiek siła (F) działa na ciało, które spoczywa w taki sposób, że wpada w ruch, możemy mówić o wykonywaniu pracy dA. Wartość tej energii dE będzie wyższa, im więcej pracy zostanie wykonanych. W tym przypadku obowiązuje równość: dA = dE.
Biorąc pod uwagę ścieżkę przebytą przez ciało (dR) i jego prędkość (dU), można zastosować prawo 2 Newtona, na podstawie którego: F = (dU / dE) * m.
Powyższe prawo stosuje się tylko wtedy, gdy istnieje bezwładnościowy układ odniesienia. Jest jeszcze jeden ważny niuans, który jest brany pod uwagę w obliczeniach. Na wartość energii wpływa wybór systemu. Tak więc, zgodnie z systemem SI, jest on mierzony w dżulach (J). Energia kinetyczna ciała charakteryzuje się masą m, a także prędkością ruchu υ. W tym przypadku będzie to: E k = ((υ * υ) * m) / 2.
W oparciu o powyższy wzór można wywnioskować, że energia kinetyczna jest określana przez masę i prędkość. Innymi słowy, jest to funkcja ruchu ciała.
Energia w systemie mechanicznym
 Energia kinetyczna jest energia mechaniczna system. To zależy od prędkości jego punktów. Mając dowolną energię punkt materialny jest reprezentowany przez następujący wzór: E = 1 / 2mυ 2, gdzie m jest masą punktu, a υ jest jego prędkością.
Energia kinetyczna jest energia mechaniczna system. To zależy od prędkości jego punktów. Mając dowolną energię punkt materialny jest reprezentowany przez następujący wzór: E = 1 / 2mυ 2, gdzie m jest masą punktu, a υ jest jego prędkością.
Energia kinetyczna układu mechanicznego jest sumą arytmetyczną tych samych energii ze wszystkich jej punktów. Można to również wyrazić za pomocą następującego wzoru: E k = 1 / 2Mυ c2 + Ec, gdzie υc jest prędkością środka masy, M jest masą układu, Ec jest energią kinetyczną układu podczas poruszania się po środku masy.
Solidna energia
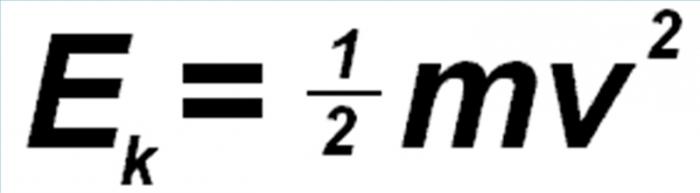 Energię kinetyczną ciała, która porusza się progresywnie, określa ta sama energia punktu o masie równej masie całego ciała. Do obliczania wskaźników podczas przenoszenia stosuje się bardziej złożone formuły. Zmiana tej energii układu w momencie jego przemieszczania się z jednej pozycji do drugiej następuje pod wpływem przyłożonych sił wewnętrznych i zewnętrznych. Jest równy sumie pracy Aue i A'u tych sił podczas tego ruchu: E2 - E1 = Au Aue + Σu A'u.
Energię kinetyczną ciała, która porusza się progresywnie, określa ta sama energia punktu o masie równej masie całego ciała. Do obliczania wskaźników podczas przenoszenia stosuje się bardziej złożone formuły. Zmiana tej energii układu w momencie jego przemieszczania się z jednej pozycji do drugiej następuje pod wpływem przyłożonych sił wewnętrznych i zewnętrznych. Jest równy sumie pracy Aue i A'u tych sił podczas tego ruchu: E2 - E1 = Au Aue + Σu A'u.
Ta równość odzwierciedla twierdzenie dotyczące zmiany energii kinetycznej. Za jego pomocą rozwiązywane są najróżniejsze problemy mechaniki. Bez tej formuły nie da się rozwiązać wielu ważnych zadań.
Energia kinetyczna przy dużych prędkościach
Jeśli prędkość ciała jest zbliżona do prędkości światła, energia kinetyczna punktu materialnego może być obliczona według następującego wzoru:
E = m0c2 / √1-υ2 / c2 - m0c2,
gdzie c jest prędkością światła w próżni, m0 jest masą punktu, m0c2 jest energią punktu. Przy niskiej prędkości (υ Podczas obrotu ciała wokół osi każda z jego podstawowych objętości (mi) opisuje okrąg o promieniu ri. W tym momencie objętość ma prędkość liniową υi. Ponieważ bierze się pod uwagę ciało stałe, prędkość kątowa obrót wszystkich woluminów będzie taki sam: ω = υ1 / r1 = υ2 / r2 = ... = υn / rn (1). Energia kinetyczna rotacji bryły jest sumą wszystkich tych samych energii jej objętości elementarnych: E = m1υ1 2/2 + miυi 2/2 + ... + mnustom 2/2 (2). Przy użyciu wyrażenia (1) otrzymujemy wzór: E = Jz ω 2/2, gdzie Jz jest momentem bezwładności ciała wokół osi Z. Porównując wszystkie formuły, staje się jasne, że moment bezwładności jest miarą bezwładności ciała podczas ruch obrotowy. Wzór (2) jest odpowiedni dla obiektów obracających się wokół stałej osi. Energia kinetyczna ciała poruszającego się w dół płaszczyzny składa się z energii rotacji i ruchu postępowego: E = mυc2 / 2 + Jz ω 2/2, gdzie m jest masą poruszającego się ciała, Jz jest momentem bezwładności ciała wokół osi, υc jest prędkością środka masy, ω jest prędkością kątową. Zmiana wartości energii kinetycznej jest ściśle związana z potencjałem. Istotę tego zjawiska można zrozumieć za pomocą prawa zachowania energii w systemie. Suma E + dP podczas ruchu ciała zawsze będzie taka sama. Zmiana wartości E następuje zawsze równocześnie ze zmianą dP. W ten sposób są one przekształcane, jakby napływały do siebie nawzajem. Takie zjawisko można znaleźć w prawie wszystkich układach mechanicznych. W celu obliczenia wartości energetycznej wybierany jest arbitralny moment (uważany za początkowy) i układ odniesienia. Możliwe jest określenie dokładnej ilości energii potencjalnej tylko w strefie oddziaływania sił, które nie zależą od trajektorii ciała podczas wykonywania pracy. W fizyce siły te nazywa się konserwatywnymi. Mają stały związek z prawem zachowania energii. Jeżeli wpływ zewnętrzny jest minimalny lub zredukowany do zera, badany system będzie zawsze w stanie, w którym jego energia potencjalna również będzie miała tendencję do zera. Na przykład, rzucona kula osiągnie granicę tej energii w górnym punkcie trajektorii ruchu iw tym samym momencie zacznie spadać. W tym czasie nagromadzona energia w locie zamienia się w ruch (praca wykonywana). W każdym razie w przypadku energii potencjalnej występuje interakcja przynajmniej dwóch ciał (w przykładzie z kulą wpływa na nią grawitacja planety). Energia kinetyczna może być obliczana indywidualnie dla każdego poruszającego się ciała. Potencjał i energia kinetyczna zmieniają się wyłącznie w interakcji ciał, gdy siła działająca na ciało wykonuje pracę, której wartość jest różna od zera. W układzie zamkniętym działanie siły lub elastyczności jest równe zmianie energii potencjalnej obiektów ze znakiem "-": A = - (Ep2 - Ep1). Praca siły lub elastyczności jest równa zmianie energii: A = Ek2 - Ek1. Z porównania obu równań jasno wynika, że zmiana energii obiektów w układzie zamkniętym jest równa zmianie energii potencjalnej i jest przeciwna w znaku: Ek2 - Ek1 = - (Ep2 - Ep1) lub inaczej: Ek1 + Ep1 = Ek2 + Ep2. Z tej równości jasno wynika, że suma tych dwóch energii ciał w zamkniętym układzie mechanicznym i oddziaływujących siłach sprężystości i agresji zawsze pozostaje stała. Na podstawie powyższego można stwierdzić, że w procesie badania układu mechanicznego należy rozważyć wzajemne oddziaływanie energii potencjalnej i kinetycznej. 
Energia rotacyjna systemu
Planarny ruch ciała

Zmiana energii w układzie mechanicznym
Połączenie energetyczne
Potencjał i energia kinetyczna są ze sobą ściśle powiązane. Ich suma może być przedstawiona jako całkowita energia systemu. Na poziomie molekularnym jest energia wewnętrzna ciało. Jest stale obecny, o ile zachodzi przynajmniej jakaś interakcja między ciałami i ruch termiczny. Wybór systemu odniesienia
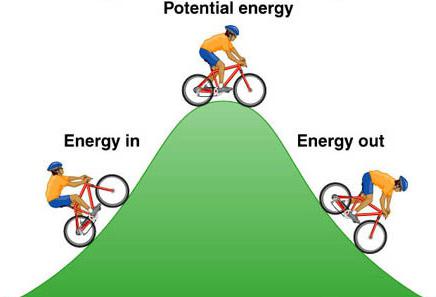
Istota różnicy między potencjałem a energią kinetyczną
Połączenie różnych energii