Równania liniowe: formuły i przykłady. Nierówności i ich rozwiązanie
Nauka rozwiązywania równań jest jednym z głównych zadań, jakie algebra stawia uczniom. Zaczynając od najprostszego, gdy składa się z jednej nieznanej i przechodzącej do coraz bardziej złożonej. Jeśli działania, które trzeba wykonać z równaniami z pierwszej grupy, nie są zrozumiałe, trudno będzie poradzić sobie z innymi.
Aby kontynuować rozmowę, musisz zgodzić się na notację.
| Nazwa wartości | Jego oznaczenie |
| zmienna | x, y |
| dowolna liczba | a, b, c |
Widok ogólny równania liniowego z nieznanym i zasada jego rozwiązania
Każde równanie, które może prowadzić do zapisu tego typu:
a * x = w ,
nazywany liniowym . To jest ogólny wzór. Ale często w zadaniach równania liniowe są pisane niejawnie. Następnie musisz wykonać identyczne transformacje, aby uzyskać ogólnie akceptowany zapis. Działania te obejmują:
Ad
- nawiasy otwierające;
- przesuwanie wszystkich pojęć ze zmienną po lewej stronie równania, a reszta po prawej;
- przynoszenie takich warunków.
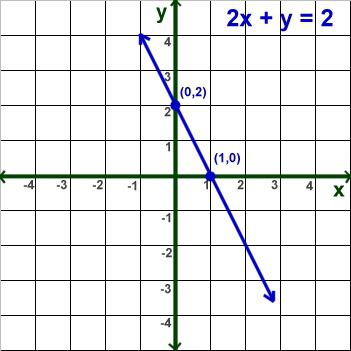
W przypadku gdy nieznana wartość jest w mianowniku ułamka, konieczne jest określenie jej wartości, przy których wyrażenie nie będzie miało sensu. Innymi słowy, konieczne jest poznanie dziedziny równania.
Zasada, dzięki której wszystkie równania liniowe są rozwiązywane, zmniejsza się do dzielenia wartości po prawej stronie równości przez współczynnik przed zmienną. Oznacza to, że "x" będzie równe / a.
Szczególne przypadki równania liniowego i ich rozwiązania
Podczas wnioskowania takie momenty mogą powstać, gdy równania liniowe przyjmują jeden ze specjalnych typów. Każdy z nich ma konkretne rozwiązanie.
W pierwszej sytuacji:
a * x = 0 , ponadto a ≠ 0.
Rozwiązaniem takiego równania będzie zawsze x = 0.
W drugim przypadku "a" przyjmuje wartość równą zeru:
0 * x = 0 .
Odpowiedź na to równanie będzie dowolną liczbą. Oznacza to, że ma nieskończoną liczbę korzeni.
Trzecia sytuacja wygląda następująco:
0 * x = w , gdzie w ≠ 0.
To równanie nie ma sensu. Ponieważ korzenie, które go zadowalają, nie istnieją.

Widok ogólny równania liniowego z dwiema zmiennymi
Od jego nazwy staje się jasne, że istnieją już dwie nieznane wielkości. Równania liniowe z dwiema zmiennymi wyglądają tak:
a * x + v * y = s .
Ponieważ w rekordzie są dwie niewiadome, odpowiedź będzie wyglądać jak para cyfr. To nie wystarczy, aby podać tylko jedną wartość. To będzie niekompletna odpowiedź. Para wielkości, w których równanie zamienia się w tożsamość, jest rozwiązaniem równania. Co więcej, odpowiedź jest zawsze pierwszą, która zapisuje zmienną, która pojawia się wcześniej w kolejności alfabetycznej. Czasami mówią, że te liczby go satysfakcjonują. Ponadto takie pary mogą być nieskończoną liczbą.
Ad
Jak rozwiązać równanie liniowe z dwoma niewiadomymi?
Aby to zrobić, po prostu wybierz dowolną parę liczb, która okazuje się prawdą. Dla uproszczenia możesz przyjąć jedną z niewiadomych równą dowolnemu liczba pierwsza a następnie znajdź drugi.
W rozwiązywaniu często konieczne jest wykonanie działań upraszczających równanie. Nazywane są transformacjami tożsamości. Ponadto następujące właściwości są zawsze ważne dla równań:
- każdy termin może zostać przeniesiony na przeciwną część równości poprzez zastąpienie jej znakiem przeciwnym;
- lewa i prawa strona dowolnego równania mogą być podzielone przez tę samą liczbę, jeśli nie jest równa zeru.

Przykłady zadań z równaniami liniowymi
Pierwsze zadanie. Rozwiąż równania liniowe: 4x = 20, 8 (x - 1) + 2x = 2 (4 - 2x); (5x + 15) / (x + 4) = 4; (5x + 15) / (x + 3) = 4.
W równaniu, które pojawia się jako pierwsze na tej liście, wystarczy podzielić po prostu 20 na 4. Wynik wyniesie 5. To jest odpowiedź: x = 5.
Trzecie równanie wymaga przeprowadzenia transformacji tożsamości. Polegać to będzie na ujawnieniu nawiasów i wprowadzeniu takich terminów. Po pierwszym działaniu równanie przyjmuje postać: 8x - 8 + 2x = 8 - 4x. Następnie musisz przenieść wszystkie niewiadome na lewą stronę równości, a resztę po prawej. Równanie będzie wyglądało następująco: 8x + 2x + 4x = 8 + 8. Po zmniejszeniu takich terminów: 14x = 16. Teraz wygląda tak samo jak pierwsze, a jego rozwiązanie jest łatwe. Odpowiedź brzmi: x = 8/7. Ale w matematyce ma przypisać całą część niewłaściwa frakcja. Następnie wynik zostanie przekształcony, a "x" będzie równe jednej całości i jednej siódmej.
Ad
W pozostałych przykładach zmienne są w mianowniku. Oznacza to, że najpierw musisz wiedzieć, jakie wartości są zdefiniowane. W tym celu należy wykluczyć liczby, przy których mianowniki zwracają się do zera. W pierwszym przykładzie jest to "-4", w drugim - "-3". Oznacza to, że wartości te muszą zostać wykluczone z odpowiedzi. Następnie należy pomnożyć obie strony równania przez wyrażenia w mianowniku.
Otwierając nawiasy i podając podobne terminy, w pierwszym z tych równań otrzymujemy: 5x + 15 = 4x + 16, a w drugim 5x + 15 = 4x + 12. Po przekształceniach rozwiązaniem pierwszego równania jest x = -1. Drugi jest równy "-3", co oznacza, że ten ostatni nie ma rozwiązań.
Drugie zadanie. Rozwiąż równanie: -7x + 2y = 5.
Załóżmy, że pierwsze nieznane x = 1, to równanie przyjmuje postać -7 * 1 + 2y = 5. Po przeniesieniu współczynnika "-7" na prawą stronę równania i zmianie jego znaku na plus, okazuje się, że 2u = 12. Stąd, y = 6. Odpowiedź: jednym z rozwiązań równania jest x = 1, y = 6.
Ad

Ogólny obraz nierówności z jedną zmienną
Wszystkie możliwe sytuacje nierówności przedstawiono tutaj:
- a * x> in;
- a * x <v;
- a * x ≥ in;
- a * x ≤в.
Ogólnie rzecz biorąc wygląda to na najprostsze równanie liniowe, tylko znak równości jest zastępowany przez nierówność.
Identyczne reguły transformacji nierówności
Podobnie jak równania liniowe i nierówności mogą być modyfikowane zgodnie z pewnymi prawami. Sprowadzają się do następujących:
- dowolne wyrażenie dosłowne lub liczbowe można dodać do lewej i prawej strony nierówności, przy czym znak nierówności pozostaje taki sam;
- możliwe jest również pomnożenie lub podzielenie przez tę samą liczbę dodatnią, ponownie znak się nie zmienia;
- podczas mnożenia lub dzielenia przez tę samą liczbę ujemną, równość pozostanie prawdą pod warunkiem, że znak nierówności zostanie odwrócony.

Ogólny pogląd na podwójne nierówności
Poniższe problemy z nierównościami mogą być reprezentowane w problemach:
- w <a * x <s;
- w ≤ a * x <s;
- w <a * x ≤ s;
- w ≤ a * x ≤ c.
Podwójnie nazywa się, ponieważ jest ograniczona przez oznaki nierówności po obu stronach. Jest rozwiązywany przy użyciu tych samych zasad, co zwykłe nierówności. A znalezienie odpowiedzi sprowadza się do kilku identycznych transformacji. Aż najprostsze zostanie odebrane.
Cechy rozwiązania podwójnych nierówności
Pierwszym z nich jest jego obraz na osi współrzędnych. Nie ma potrzeby korzystania z tej metody w przypadku prostych nierówności. Ale w trudnych przypadkach może być po prostu konieczne.
Ad
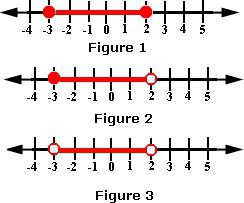
Dla obrazu nierówności konieczne jest zaznaczenie na osi wszystkich punktów, które pojawiły się w trakcie rozumowania. Są to zarówno nieprawidłowe wartości, które są oznaczone punktami przebicia, jak i wartości z nierówności uzyskanych po przekształceniach. Również tutaj ważne jest prawidłowe narysowanie punktów. Jeśli nierówność jest ścisła, to znaczy <lub>, to te wartości są przekłute. W słabych nierównościach punkty muszą być kolorowe.
Następnie należy wyznaczyć znaczenie nierówności. Można to zrobić za pomocą kreskowania lub łuków. Ich przecięcie wskaże odpowiedź.
Druga cecha jest związana z jego rekordem. Oto dwie opcje. Pierwsza to ostateczna nierówność. Drugi ma postać luk. Zdarza się, że pojawiają się trudności. Przedziały odpowiedzi zawsze wyglądają jak zmienna ze znakiem przynależności i nawiasami z liczbami. Czasami jest kilka przerw, a następnie między nawiasami trzeba wpisać symbol "i". Te znaki są następujące: ∈ i ∩. Podobnie rzecz się ma z nawiasami dystansowymi. Okrągłe jest ustawiane, gdy punkt jest wykluczony z odpowiedzi, a prostokątny zawiera tę wartość. Znak nieskończoności znajduje się zawsze w nawiasie.
Przykłady rozwiązywania nierówności
1. Rozwiąż nierówność 7 - 5x ≥ 37.
Po prostych transformacjach okazuje się, że: -5x ≥ 30. Podzielenie przez "-5" daje następujące wyrażenie: x ≤ -6. To jest odpowiedź, ale można ją zapisać w inny sposób: x ∈ (-∞; -6).
2. Rozwiąż podwójną nierówność -4 <2x + 6 ≤ 8.
Po pierwsze, musisz odjąć wszędzie 6. Okazuje się: -10 <2x ≤ 2. Teraz musisz podzielić przez 2. Nierówność będzie wyglądać następująco: -5 <x ≤ 1. Po przedstawieniu odpowiedzi na osi liczbowej możesz od razu zrozumieć, że wynik będzie od -5 do 1. I pierwszy punkt jest wykluczony, a drugi jest włączony. Oznacza to, że odpowiedź na nierówność to: x ∈ (-5; 1).