Twierdzenie Ostrogradsky'ego - Gaussa i wzór

Mv Ostrogradsky - rosyjski matematyk i fizyk od czasów Imperium Rosyjskiego, akademik. Wniósł ogromny wkład w rozwój analiza matematyczna teoria prawdopodobieństwa, mechanika (sekcja fizyki) teoria liczb. W 1826 roku wyprowadził formułę, obecnie nazywaną formułą Ostrogradsky-Gauss.

Historia odnajdywania

Formuła Ostrogradsky-Gauss została po raz pierwszy wymieniona przez Josepha Lagrange'a w 1762 roku.

Co więcej, główny sposób zmniejszenia potrójnej integralności powierzchni został udowodniony przez Karla Gaussa, który zastosował rozwiązanie problemów w elektrodynamice jako podstawę dla dowodu. Stało się to w pierwszej połowie XIX wieku.

Ponadto formułę w ogólnej formie przedstawił Mikhail Ostrogradsky. Przy jego pomocy stało się możliwe wyrażenie wartości różnicy w parametrze z całki N-godzinnej.

Znaczenie formuły Ostrogradsky

Formuła Ostrogradsky-Gauss odnosi się do potrójnej całki ponad przestrzenną objętością z całką na powierzchni na jej powierzchni. Jest to analogia zielonej formuły, która wiąże podwójną całkę nad płaszczyzną z krzywoliniową wzdłuż jej granic.

Wyprowadzenie formuły

Ostrogradsky - Formuła Gaussa: konkluzja. Załóżmy, że w domenie W zdefiniowana jest funkcja całkowania R (x, y, z), która jest określona i ciągła. Jego pochodna jest podobna w całej domenie W, łącznie z jej granicą. W tej formie znane jest teraz twierdzenie Ostrogradsky - Gauss (wzór podany jest poniżej).

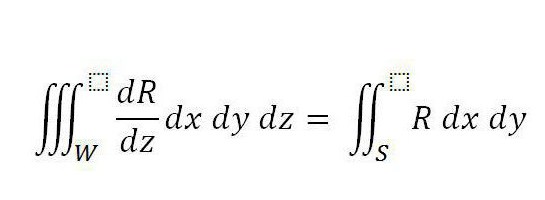
Co więcej, S jest powierzchnią, która wiąże ciało, a całka po prawej stronie jest rozłożona na jej zewnętrzną stronę.

I absolutnie prawdziwe

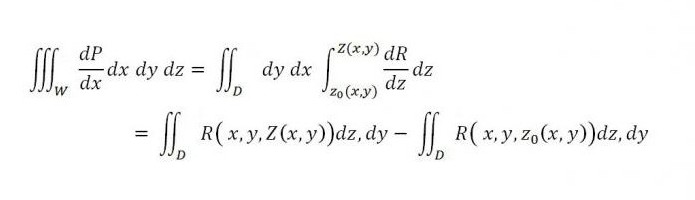
Jeśli podobnie uwzględnimy całki na powierzchni, wtedy

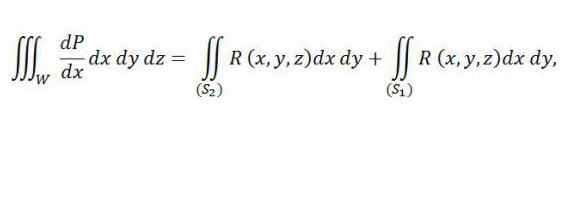
natomiast po prawej stronie jest suma dwóch całek - pierwsza jest związana z górną częścią powierzchni (S ₂ ), a druga - z dolną częścią powierzchni (S ₁ ). Jeśli dodamy wskazaną poniżej całkę do tej równości po prawej, wtedy jej ważność nie zostanie naruszona:

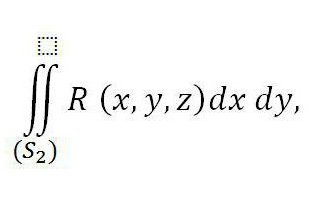
Odpowiada on zewnętrznej części powierzchni S _{3 z} powodu równości do zera.

Jeśli połączymy wszystkie trzy powyższe całki w jeden, uzyskamy specjalny przypadek wzoru Ostrogradskiego.

Łatwo jest zrozumieć, że ta formuła jest prawdziwa dla szerszej klasy ciał i jest również ważna dla liczb ograniczonych absolutnie dowolnymi nieliniowymi powierzchniami.

Następujące formuły są podobnie prawdziwe:

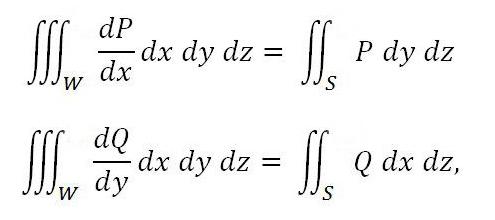
jeżeli funkcje Q i P są ciągłe w domenie wraz z ich pochodnymi dP / dx i dQ / dy.

Jeśli dodamy obie równości, otrzymamy wyrażenie dla formuły Ostrogradzkiego. Wyświetla on całkę na powierzchni, skorelowaną z zewnętrzną częścią powierzchni, poprzez potrójną całkę, która jest przejmowana przez sam korpus, którego granicą jest wspomniana wyżej powierzchnia.

Należy rozumieć, że formuły Green, Stokes i Ostrogradsky wyrażają integralną całość związaną z pewnym ciałem geometrycznym, poprzez całkę, która jest brana na jego granicę. Formułę zieloną stosuje się tylko w przypadku dwuwymiarowości przestrzeni, formułę Stokesa stosuje się do zakrzywionej przestrzeni dwuwymiarowej.

Formułę Newtona-Leibniza można również uważać za pewien analog tych formuł, ale za jednowymiarową przestrzeń.

Zastosowanie tej formuły

Niech ciągłe funkcje A, B i C będą podane w niezamkniętym obszarze przestrzeni, biorąc dowolną zamkniętą powierzchnię, która jest w danym regionie i ograniczając pewne ciało, możemy wziąć pod uwagę następującą całkę na powierzchni:

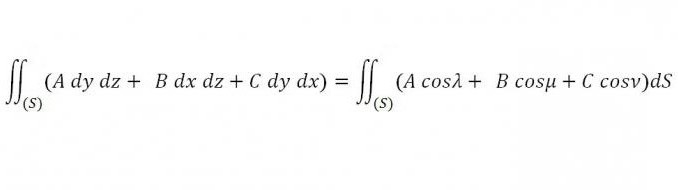
Konieczne jest znalezienie takich wartości A, B i C, aby dla wszystkich x, yi z tej całki była równa zero.

Aby to zrobić, użyj formuły Ostrogradsky-Gauss. Jednym z domniemanych warunków jest pewność i ciągłość funkcji A, B i C oraz ich pochodnych.

Wymagane jest również konkretne wprowadzenie najbardziej danego ograniczenia dla danego przypadku: zarówno ciało, jak i powierzchnia, która je ogranicza, muszą być zawarte jednocześnie w określonym i określonym obszarze, zwanym po prostu połączonym. Jego główną cechą jest brak pustej przestrzeni (w tym przestrzeni punktowej). Tak więc granica ciała będzie jedna, a wraz z nią pojedyncza powierzchnia.

Po zastosowaniu formuły można uzyskać następujący warunek, który jest wystarczający:

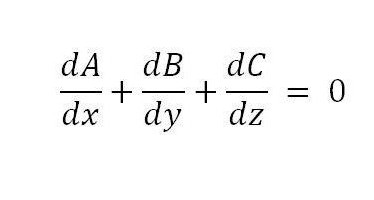
Aby udowodnić, że warunek jest również konieczny, wystarczy użyć zróżnicowania całki potrójnej.

Podsumowując, należy powiedzieć o obszarach zastosowania.

Jak w praktyce stosuje się formułę Ostrogradsky-Gauss? Przykłady użycia można znaleźć na różnych polach: wyprowadzić niektóre formuły z fizyki (na przykład równanie dyfuzji), całki transformacyjne, obliczyć całki Gaussa, udowodnić pewne formuły i wiele więcej.