Przegląd różnych typów pryzmatów. Właściwości pryzmatów trójkątnych
Pryzmat jest jedną ze słynnych postaci w przestrzeni, której właściwości są szczegółowo badane w szkolnym kursie geometrii. W tym artykule omówiono różne typy pryzmatów i ich cechy. Charakterystyki trójkątnego pryzmatu są opisane bardziej szczegółowo.
Czym jest pryzmat?
Artykuł zaczyna się od definicji pryzmatu w geometrii. Pod nim figura powinna być utworzona przez dwa identyczne równoległe boki, które są płaskimi n-gonami, oraz n boków równoległoboku. Każdy kształt, który spełnia zapisaną definicję, będzie pryzmatem.
Zbuduj pryzmat za pomocą operacji geometrycznych nie jest trudne. Trzeba tylko wziąć absolutnie dowolny n-gon i przenieść go równolegle do siebie dla pewnego segmentu w przestrzeni.
Ponieważ figurą jest wielościan (składa się z wielobocznych powierzchni), nie można go geometrycznie uzyskać przez obrót, jak to jest możliwe dla cylindra lub stożka.
Każdy pryzmat ma dwie podstawy, które są reprezentowane przez równe n-gony i n równoległoboków (czasami mogą to być prostokąty, kwadraty lub romby), których całość tworzy boczną powierzchnię figury. Również figura charakteryzuje się 2 * n równymi wierzchołkami i 3 * n krawędziami, gdzie n jest liczbą boków (wierzchołków) wielobocznej podstawy.
W jaki sposób klasyfikowane są pryzmaty?
Liczba różnych pryzmatów jest nieskończona. Wszystkie różnią się od siebie kształtem i wymiarami liniowymi, jednak istnieją tylko dwie cechy ich struktury geometrycznej, które są podstawą współczesnej klasyfikacji klasy danych liczb. Te funkcje są następujące:
- podstawowy typ wielokąta;
- kąty między bokami i podstawami.
Żadne inne parametry niż te wspomniane powyżej nie wpływają na wygląd pryzmatu. Obie cechy razem prowadzą do podziału całej klasy na cztery typy lub typy liczb:
- wypukłe i wklęsłe;
- trójkątne czworokątne, ..., n-węgiel;
- prosty i pochyły;
- dobro i zło.
Rozważmy bardziej szczegółowo każdy z tych typów pryzmatów, których właściwości są jednoznacznie określone przez powyższą klasyfikację.
Wypukłe i wklęsłe figurki
Wiele osób zapomina o tym punkcie klasyfikacji, gdy charakteryzują pryzmaty, ponieważ we wszystkich problemach geometrycznych z reguły pojawiają się wyraźne liczby. Tak więc nazywamy wypukły pryzmat, który u podstawy ma wypukły wielokąt. Odpowiednio, jeśli wielokąt jest wklęsły, pryzmat będzie również wklęsły.
W dalszej części artykułu pokazane zostaną tylko wypukłe pryzmaty, ale tutaj pokażemy na przykład, jak wygląda wklęsły pryzmat w kształcie gwiazdy.
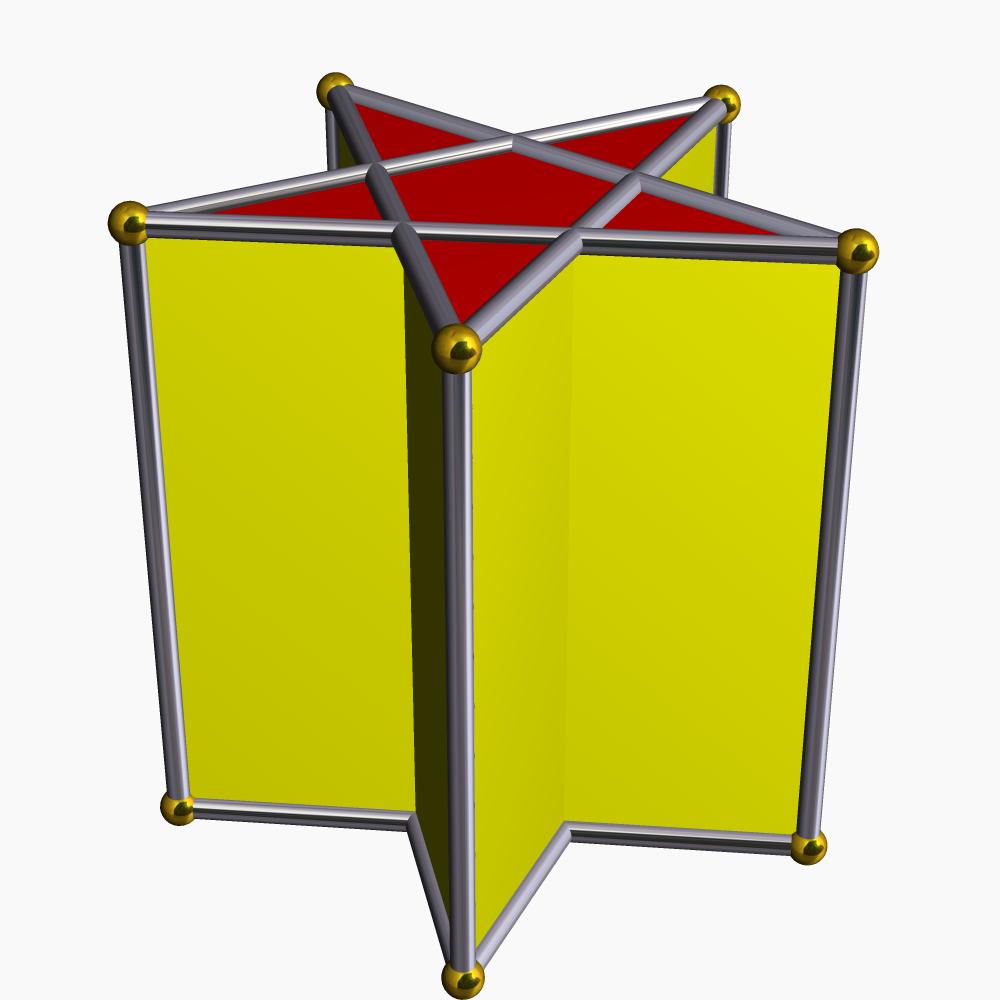
Zwróć uwagę, że wklęsły pryzmat z minimalną liczbą boków u podstawy będzie miał kształt czworokątny, podczas gdy dla wypukłego pryzmatu ma kształt trójkąta.
Pryzmy wielokątne
Być może jest to najbardziej znany rodzaj pryzmatów klasyfikacji przedmiotów. Trójkątne, czworokątne, pięciokątne itd. Pryzmaty będą nazywane figurami, które mają odpowiedni wielokąt w podstawie. Na przykład na rysunku pokazano 6 różnych pryzmatów - od trójkątnego do ośmiokątnego.
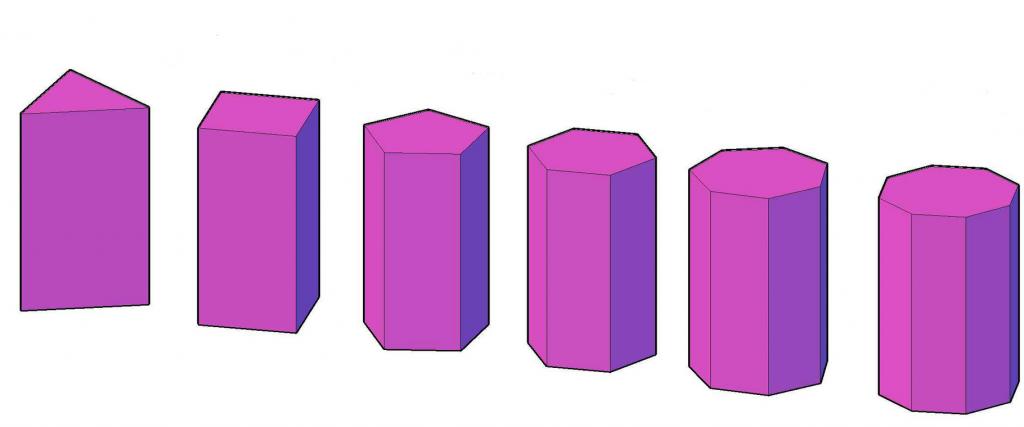
Spośród wszystkich rodzajów pryzmatów wielokątnych tylko czworokąt ma własną nazwę - równoległościan. Ten ostatni, z pewnymi parametrami liniowymi i kątowymi, może stać się sześcianem.
Ukośne i proste figury
Klasyfikacja ukośnych i bezpośrednich pryzmatów opiera się na dwuściennych kątach między bokami figury i jej podstawy. Jeśli wszystkie te kąty dwuścienne są równe 90 o , pryzmat będzie nazywany prostym lub prostokątnym. Jeśli co najmniej jeden kąt dwuścienny nie jest prawidłowy, wówczas figurę uważa się za nachyloną lub ukośną. Przypomnijmy, że mówimy tylko o kątach dwuściennych między podstawą a bokami. Kąty dwuścienne tylko między bokami nie są brane pod uwagę.
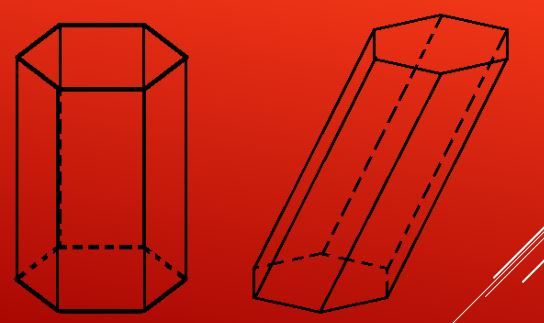
Powyższe pokazuje, jak wyglądają skośne i proste sześciokątne graniastosłupy. Rysunek pokazuje, że boki pryzmatu to prostokąty (kwadraty). Różne typy bezpośrednich pryzmatów i ukośne można uzyskać zmieniając liczbę boków wielokątów w ich podstawie.
Dobre i złe liczby
Mówiąc prościej, jeśli pryzmat jest prosty, a jego podstawa jest poprawna n-gon, to również będzie poprawna. Wszystkie inne pryzmaty, które nie spełniają opisanych warunków, są nieprawidłowe.
Powyższy rysunek, przedstawiający sześć wielokątnych pryzmatów, pokazuje regularne kształty.
Dogodne jest badanie własności pryzmatów regularnych, ponieważ dla każdego z nich istnieją określone formuły do określania ich wysokości, powierzchni, objętości, długości przekątnej i innych cech.
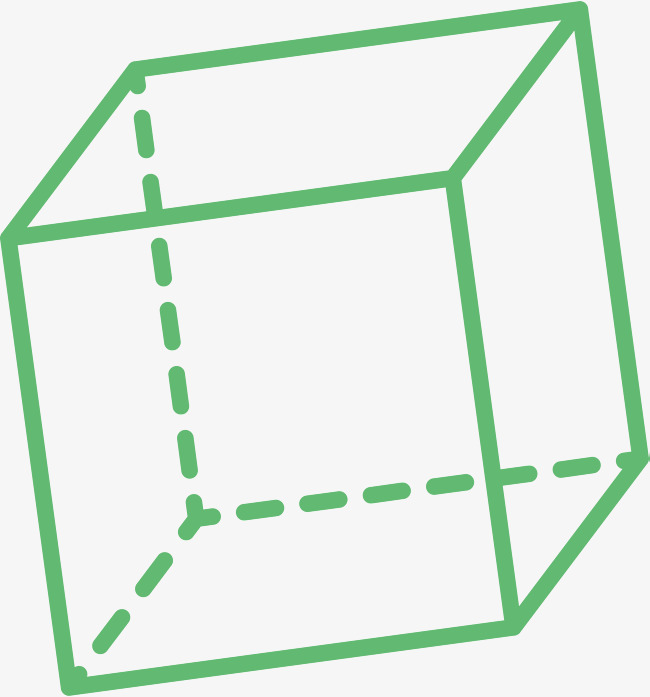
Regularny czworokątny pryzmat, którego wysokość jest równa stronie jego podstawy, nazywany jest sześcianem.
Trójkątne pryzmaty
Zajmijmy się trójkątnymi pryzmatami, ponieważ są one najprostsze spośród rozważanych postaci.

Każdy taki kształt ma 5 ścian, 6 równych wierzchołków i 9 krawędzi. Ilości trójkątnych graniastosłupów są obliczane przy użyciu wzoru obowiązującego dla dowolnych pryzmatów. Wygląda to tak:
V = S o * h.
Objętość jest równa iloczynowi powierzchni jednej podstawy i wysokości figury. W przypadku zwykłego pryzmatu z bokiem a trójkąta, wzór ten ma postać:
V = √3 / 4 * a 2 * godz.
Biorąc pod uwagę rodzaj pryzmatów, pole powierzchni trójkątnych graniastosłupów definiuje się jako sumę obszarów dwóch identycznych trójkątów i trzech równoległoboków. Jeśli jest to prawidłowy pryzmat, obowiązuje następujący wzór pola powierzchni S:
S = √3 / 2 * a 2 + 3 * a * h.
Pisząc to wyrażenie użyliśmy tego, że we właściwym pryzmie wszystkie boki są sobie równe i są prostokąty.