Równoległość samolotów: znak, warunek
Każdy, kto kiedykolwiek studiował lub obecnie studiuje w szkole, musiał zmierzyć się z różnymi trudnościami w badaniu dyscyplin, które są zawarte w programie opracowanym przez Ministerstwo Edukacji.
Jakie trudności napotykają
Nauka języków towarzyszy zapamiętywaniu istniejących reguł gramatycznych i głównych wyjątków od nich. Wychowanie fizyczne wymaga wielu obliczeń, sprawności fizycznej i cierpliwości studentów.
Niemożliwe jest jednak porównanie z wszelkimi trudnościami, które pojawiają się podczas badania dokładnych dyscyplin. Algebra zawierająca skomplikowane sposoby rozwiązywania elementarnych problemów. Fizyka z bogatym zestawem formuł praw fizyki. Geometria i jej sekcje, oparte na złożonych twierdzeniach i aksjomatach.
Przykładem są aksjomaty wyjaśniające teorię paralelizmu płaszczyzn, które należy koniecznie zapamiętać, ponieważ leżą u podstaw całego programu szkolnego w stereometrii. Spróbujmy dowiedzieć się, jak łatwo i szybciej można to zrobić.
Równoległe płaszczyzny według przykładów
Aksjomat, wskazujący na równoległość płaszczyzn, brzmi następująco: " Jakiekolwiek dwie płaszczyzny są uważane za równoległe tylko wtedy, gdy nie zawierają punktów wspólnych, tj. Nie przecinają się ze sobą. Aby wyobrazić sobie ten obraz bardziej szczegółowo, jako elementarny przykład możemy podać proporcje stropu i podłogi lub przeciwległych ścian w budynku. Natychmiast staje się jasne, co to oznacza, a także potwierdza fakt, że w zwykłym przypadku te samoloty nigdy się nie przecinają.
Innym przykładem jest szyba okienna, w której wstęgi szklane pełnią rolę płaszczyzn. W żadnym wypadku nie będą również tworzyć punktów przecięcia. Dodatkowo można dodać półki z książkami, kostkę Rubika, gdzie płaszczyzny są przeciwległymi ścianami i inne elementy codziennego życia.
Samoloty są oznaczone specjalnym znakiem w postaci dwóch prostych linii "||", które wyraźnie ilustrują równoległość płaszczyzn. Tak więc, stosując prawdziwe przykłady, można uzyskać wyraźniejsze postrzeganie tematu, a w konsekwencji można przejść do rozważań o bardziej złożonych koncepcjach.
Gdzie i jak stosuje się teorię równoległych płaszczyzn?
Studiując szkolny kurs geometrii, uczniowie stają przed wielostronnymi problemami, w których często konieczne jest określenie równoległości linii, linii i płaszczyzn między sobą lub zależności między sobą. Analizując istniejący stan, każde zadanie można skorelować z czterema głównymi klasami stereometrii.
Pierwsza klasa zawiera zadania, w których stanie konieczne jest określenie równoległości linii i płaszczyzny między sobą. Jego rozwiązanie ogranicza się do udowodnienia twierdzenia o tej samej nazwie. Aby to zrobić, należy ustalić, czy w tej płaszczyźnie znajduje się równoległa linia prosta dla linii prostej, która nie należy do danej płaszczyzny.
Druga klasa zadań obejmuje te, w których bierze udział cecha równoległości samolotów. Służy on upraszczaniu procesu dowodzenia, co znacznie skraca czas potrzebny na znalezienie rozwiązania.
Kolejna klasa obejmuje szereg problemów zgodności z bezpośrednimi podstawowymi właściwościami równoległości płaszczyzn. Rozwiązanie problemów czwartej klasy polega na ustaleniu, czy spełniony jest warunek paralelizmu samolotów. Wiedząc dokładnie, w jaki sposób pojawia się dowód konkretnego problemu, uczniowie łatwiej się poruszają, korzystając z ich istniejącego arsenału aksjomatów geometrycznych.
Zatem zadania, których stan wymaga zdefiniowania i udowodnienia równoległości linii prostych, linii prostej i płaszczyzny lub dwóch płaszczyzn między sobą, sprowadza się do prawidłowego doboru twierdzenia i rozwiązania zgodnie z istniejącym zbiorem zasad.
O równoległości linii i płaszczyzny
Równoległość linii prostej i płaszczyzny jest szczególnym tematem w stereometrii, ponieważ jest to podstawowa koncepcja, na której opierają się wszystkie kolejne właściwości równoległości figur geometrycznych.
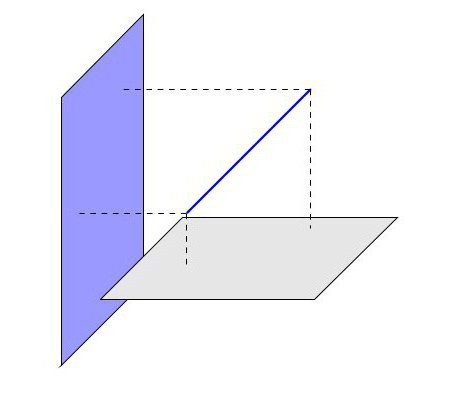
Zgodnie z istniejącymi aksjomatami, w przypadku, gdy dwa punkty linii prostej należą do pewnej płaszczyzny, możemy wywnioskować, że ta linia prosta również w niej leży. W tej sytuacji staje się jasne, że istnieją trzy opcje lokalizacji linii prostej względem płaszczyzny w przestrzeni:
- Linia należy do samolotu.
- Dla linii prostej i płaszczyzny istnieje jeden wspólny punkt przecięcia.
- Dla linii prostej i płaszczyzny punkty przecięcia są nieobecne.
W szczególności jesteśmy zainteresowani tą drugą opcją, gdy nie ma punktów przecięcia. Tylko wtedy możemy powiedzieć, że linia prosta i płaszczyzna względem siebie są równoległe. Tym samym potwierdza się warunek głównego twierdzenia o równoległym znaku prostej i płaszczyzny, który stwierdza, że: "Jeżeli prosta, która nie należy do rozważanej płaszczyzny, jest równoległa do dowolnej prostej na tej płaszczyźnie, to prosta jest również równoległa do tej płaszczyzny".
Konieczność korzystania z funkcji równoległości
Znak równoległości samolotów z reguły służy do poszukiwania uproszczonego rozwiązania problemów dotyczących samolotów. Istota tej cechy jest następująca: " Jeżeli w jednej płaszczyźnie znajdują się dwie przecinające się linie proste, równoległe do dwóch linii prostych należących do innej płaszczyzny, wówczas takie płaszczyzny można nazwać równoległymi ."
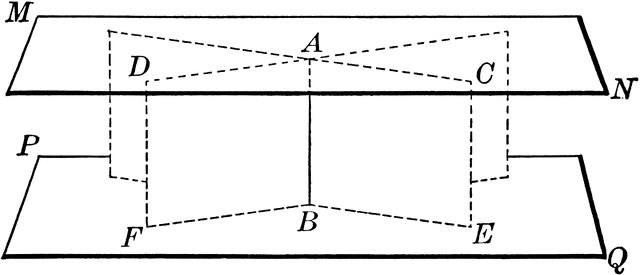
Dodatkowe twierdzenia
Oprócz używania znaku potwierdzającego paralelizm płaszczyzn, w praktyce można spotkać się z użyciem dwóch innych dodatkowych twierdzeń. Pierwszy z nich jest przedstawiony w następującej formie: " Jeśli jedna z dwóch równoległych płaszczyzn jest równoległa do trzeciej, druga płaszczyzna jest albo równoległa do trzeciej, albo całkowicie się z nią pokrywa ".
Opierając się na zastosowaniu twierdzeń redukowalnych, zawsze można udowodnić równoległość płaszczyzn w odniesieniu do rozważanej przestrzeni. Drugie twierdzenie pokazuje zależność płaszczyzn na prostopadłej linii prostej i wygląda następująco: " Jeśli dwie niepowiązujące płaszczyzny są prostopadłe w stosunku do jakiejś linii prostej, wówczas są one uważane za równoległe względem siebie ".
Pojęcie niezbędnych i wystarczających warunków
Przy kilkukrotnym rozwiązywaniu problemów z paralelizmem płaszczyzn uzyskano niezbędny i wystarczający warunek równoległości płaszczyzn. Wiadomo, że dowolną płaszczyznę daje równanie parametryczne formy: A 1 x + B 1 y + C 1 z + D 1 = 0. Nasz warunek opiera się na wykorzystaniu układu równań definiujących układ płaszczyzn w przestrzeni i jest reprezentowany przez następujące sformułowanie: " Aby udowodnić paralelizm dwóch płaszczyzn, konieczne i wystarczające jest, aby układ równań opisujących te płaszczyzny był niekompatybilny, czyli nie ma rozwiązania ".
Podstawowe właściwości
Jednak przy rozwiązywaniu problemów geometrycznych użycie funkcji równoległej nie zawsze jest wystarczające. Czasami powstaje sytuacja, gdy konieczne jest udowodnienie równoległości dwóch lub więcej linii w różnych płaszczyznach lub równości segmentów zamkniętych na tych liniach. Aby to zrobić, zastosuj właściwości równoległych płaszczyzn. W geometrii są tylko dwa.
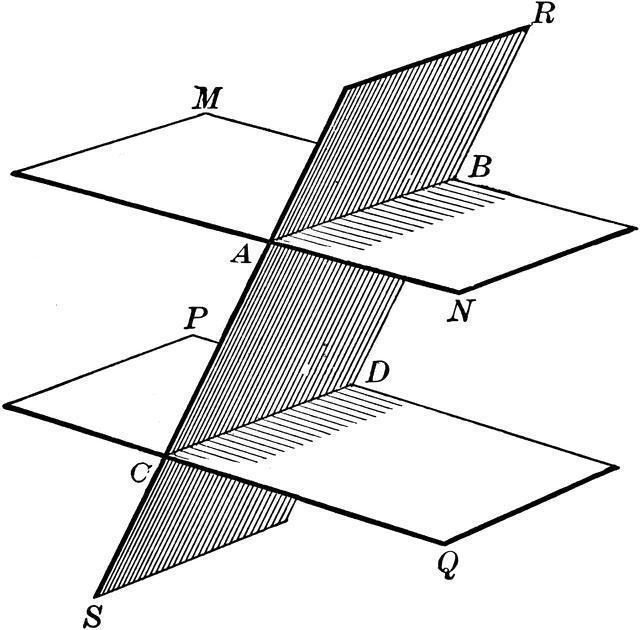
Pierwsza właściwość pozwala nam ocenić równoległość linii w pewnych płaszczyznach i jest przedstawiona w następującej formie: " Jeśli dwie równoległe płaszczyzny przecinają się z trzecią, wówczas linie utworzone przez linie przecięcia będą również równoległe do siebie ."
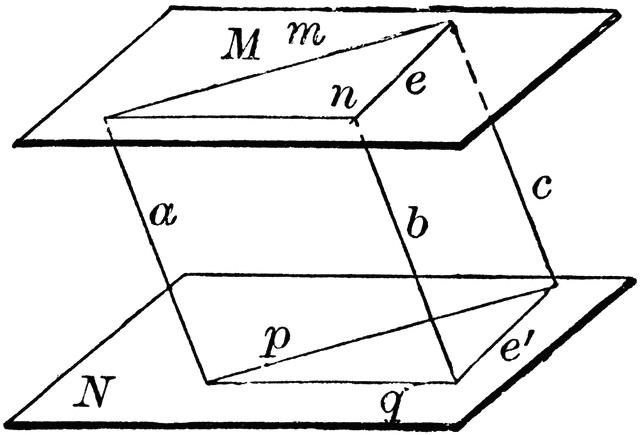
Znaczenie drugiej właściwości polega na wykazaniu równości segmentów położonych na równoległych liniach prostych. Jego interpretacja została przedstawiona poniżej. " Jeśli weźmiemy pod uwagę dwie równoległe płaszczyzny i zawarliśmy obszar między nimi, to można argumentować, że długość segmentów tworzonych przez ten region będzie taka sama ."