Ruch obrotowy ciała. Prawo ruchu obrotowego

W tym artykule opisano ważną część fizyki - "Kinematyka i dynamika ruchu obrotowego".

Podstawowe pojęcia kinematyki ruchu obrotowego

Ruch obrotowy punkt materialny wokół stałej osi nazywa się taki ruch, którego trajektoria jest kołem położonym w płaszczyźnie prostopadłej do osi, a jego środek leży na osi obrotu.

Ruch obrotowy ciała stałego jest ruchem, w którym wszystkie punkty ciała poruszają się wzdłuż koncentrycznych okręgów (których środki znajdują się na tej samej osi) zgodnie z zasadą ruchu obrotowego punktu materialnego.

Niech dowolne sztywne ciało T obraca się wokół osi O, która jest prostopadła do płaszczyzny figury. Wybierz punkt M na tym ciele. Podczas obrotu ten punkt opisuje okrąg o promieniu r wokół osi O.

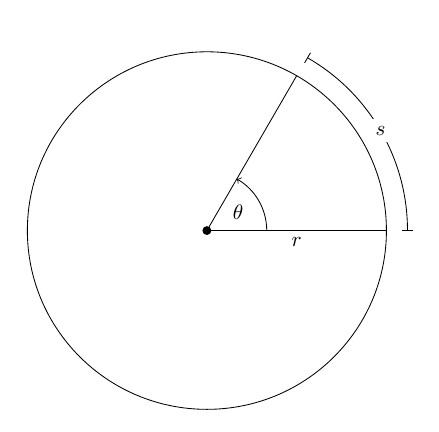
Po pewnym czasie promień obróci się względem pozycji początkowej o kąt Δφ.

Kierunek prawego wkrętu (zgodnie z ruchem wskazówek zegara) przyjmowany jest jako dodatni kierunek obrotu. Zmiana kąta obrotu z czasem nazywana jest równaniem ruchu obrotowego bryły:

φ = φ (t).

Jeżeli φ jest mierzone w radianach (1 rad jest kątem odpowiadającym łukowi o długości równej jego promieniu), to długość łuku koła ΔS, w którym punkt materialny M przejdzie w czasie Δt, jest równa:

ΔS = Δφr.

Główne elementy kinematyki jednolitego ruchu obrotowego

Miarą ruchu punktu materialnego w krótkim okresie czasu dt jest elementarny wektor obrotu dφ .

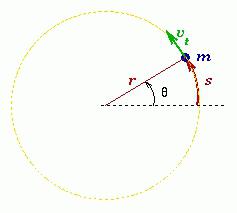
Prędkość kątowa Punkt materialny lub ciało jest wielkością fizyczną, która jest określona przez stosunek wektora obrotu elementarnego do czasu trwania tego obrotu. Kierunek wektora może być określony przez regułę prawego wkrętu wzdłuż osi O. W postaci skalarnej:

ω = dφ / dt.

Jeżeli ω = dφ / dt = const, wówczas taki ruch nazywamy jednolitym ruchem obrotowym. Kiedy jest to prędkość kątowa jest określona przez formułę

ω = φ / t.

Zgodnie ze wstępnym wzorem, wymiar prędkości kątowej

[ω] = 1 rad / s.

Jednolity ruch obrotowy ciała może być opisany przez okres rotacji. Okres obrotu T jest wielkością fizyczną, która określa czas potrzebny, aby ciało wokół osi obrotu wykonało jeden pełny obrót ([T] = 1 s). Jeśli we wzorze na prędkość kątową przyjmujemy t = T, φ = 2 π (pełny jeden obrót promienia r), to

ω = 2π / T,

dlatego okres rotacji jest zdefiniowany następująco:

T = 2π / ω.

Liczba obrotów, jaką ciało wykonuje w jednostce czasu, nazywana jest częstotliwością obrotu v, która jest równa:

ν = 1 / T.

Częstotliwości: [ν] = 1 / c = 1 s ^-1 = 1 Hz.

Porównując wzory dla prędkości kątowej i prędkości obrotowej, uzyskujemy wyrażenie odnoszące się do tych wielkości:

ω = 2πν.

Główne elementy kinematyki nierównomiernego ruchu obrotowego

Nierówny ruch obrotowy bryły lub punktu materialnego wokół stałej osi charakteryzuje prędkość kątową, która zmienia się wraz z upływem czasu.

Wektor ε , który charakteryzuje szybkość zmiany prędkości kątowej, nazywany jest wektorem przyspieszenia kątowego:

ε = dω / dt.

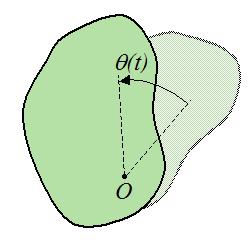
Jeśli ciało obraca się, przyspieszając, to znaczy dω / dt> 0 , wektor ma kierunek wzdłuż osi w tym samym kierunku co ω.

Jeśli ruch obrotowy jest powolny - dω / dt <0 , wówczas wektory ε i ω są skierowane przeciwnie.

Uwaga Kiedy pojawia się nierównomierny ruch obrotowy, wektor ω może zmieniać się nie tylko pod względem wielkości, ale także w kierunku (kiedy obraca się oś obrotu).

Związek wielkości charakteryzujących ruch translacyjny i rotacyjny

Wiadomo, że długość łuku z kątem obrotu promienia i jego wartości jest powiązana z

ΔS = Δφ r.

Następnie prędkość liniowa punktu materialnego wykonującego ruch obrotowy

υ = ΔS / Δt = Δφr / Δt = ωr.

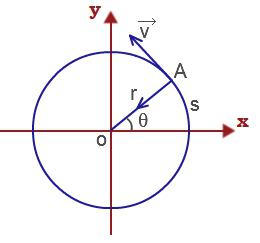
Normalne przyspieszenie punktu materialnego, który wykonuje ruch obrotowy ruch do przodu definiujemy w następujący sposób:

a = υ ² / r = ω ² r ² / r.

Tak więc w formie skalarnej

a = ω ² r.

Przyspieszony punkt materiałowy, który wykonuje ruch obrotowy

a = ε r.

Moment pędu punktu materialnego

Iloczyn wektorowy wektora promieniowego trajektorii punktu materialnego masy m _i przez jego pęd nazywany jest momentem pędu tego punktu względem osi obrotu. Kierunek wektora można określić za pomocą reguły z prawą śrubą.

Moment pędu punktu materialnego ( L _i ) jest skierowany prostopadle do płaszczyzny narysowanej przez ri _i υ _i i tworzy z nimi prawe trzy wektory (to znaczy, gdy przemieszcza się od końca wektora ri do υ _i, prawa śruba pokaże kierunek wektora L _i ).

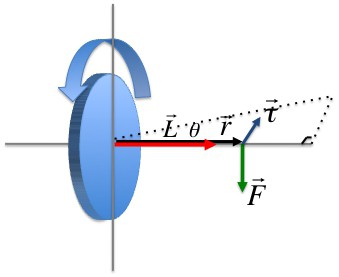
W formie skalarnej

L = m _i υ _i r _i sin (υ _{i ,} r _i ).

Biorąc pod uwagę, że podczas poruszania się w okręgu wektor promienia i wektor prędkości liniowej dla i-tego punktu materialnego są wzajemnie prostopadłe,

sin (υ _{i ,} r _i ) = 1.

Zatem moment pędu punktu materialnego dla ruchu obrotowego przybierze formę

L = m _i υ _i r _{i .}

Moment siły działający na i-tym punkcie materialnym

Produkt wektorowy wektora promieniowego, który jest utrzymywany w punkcie przyłożenia siły, przez tę siłę nazywany jest momentem siły działającej na i-tym punkcie materialnym względem osi obrotu.

W formie skalarnej

M _i = r _i F sin (r _i , F _i ).

Zakładając, że r _i sinα = l, Mi _i = l _i F _i .

Wartość l _i równą długości prostopadłej, obniżonej od punktu obrotu do kierunku siły, nazywana jest ramieniem siły F _i .

Dynamika rotacyjna

Równanie dynamiki ruchu obrotowego zapisuje się jako:

M = dL / dt.

Sformułowanie prawa jest następujące: tempo zmiany momentu pędu ciała, które obraca się wokół stałej osi, jest równe wynikowemu momentowi wokół tej osi wszystkich sił zewnętrznych przyłożonych do ciała.

Moment impulsu i moment bezwładności

Wiadomo, że dla i-tego punktu materialnego moment pędu w formie skalarnej jest podany wzorem

L _i = m _i υ _i r _{i .}

Jeśli zamiast prędkości liniowej zastąpić jej wyrażenie przez kątowe:

υ _i = ωr _i ,

wtedy wyrażenie momentu pędu przyjmuje formę

L _i = m _i r _i ² ω.

Wielkość I _i = m _i r _i ² nazywana jest momentem bezwładności wokół osi i-tego punktu materialnego bezwzględnie sztywnego ciała przechodzącego przez jego środek masy. Następnie moment pędu punktu materialnego, który piszemy:

L _i = I _i ω.

Moment impulsu absolutnie sztywnego ciała zapisany jest jako suma impulsowych momentów materialnych punktów, które składają się na to ciało:

L = Iω.

Moment siły i moment bezwładności

Prawo ruchu obrotowego brzmi następująco:

M = dL / dt.

Znany z przedstawienia chwili Impuls ciała możliwe przez moment bezwładności:

L = Iω.

Następnie

M = Idω / dt.

Biorąc pod uwagę, że przyspieszenie kątowe jest określane przez wyrażenie

ε = dω / dt,

otrzymujemy wzór na moment siły reprezentowany przez moment bezwładności:

M = Iε.

Uwaga Moment siły jest uważany za dodatni, jeśli przyspieszenie kątowe, o które jest ono spowodowane, jest większe od zera i odwrotnie.

Twierdzenie Steinera. Prawo dodawania momentów bezwładności

Jeśli oś obrotu ciała przez środek masy nie przechodzi, wtedy w odniesieniu do tej osi można znaleźć moment bezwładności zgodnie z twierdzeniem Steinera:
I = I ₀ + ma ² ,

gdzie ja ₀ - początkowy moment bezwładności ciała; m jest masą ciała; a to odległość między osiami.

Jeśli układ, który obraca się wokół stałej osi, składa się z ciał, to całkowity moment bezwładności tego typu układu będzie równy sumie momentów, które go tworzą (prawo dodawania momentów bezwładności).