Znaki, elementy składowe i własności trójkąta równoramiennego

Pierwsi historycy naszej cywilizacji - starożytni Grecy - mówią o Egipcie jako miejscu narodzin geometrii. Trudno się z nimi nie zgodzić, wiedząc z jaką niezwykłą precyzją wzniesiono gigantyczne grobowce faraonów. Wzajemne ułożenie płaszczyzn piramidy, ich proporcje, orientacja wzdłuż punktów kardynalnych - byłoby niemożliwe do osiągnięcia takiej doskonałości bez znajomości podstaw geometrii.

Słowo "geometria" można przetłumaczyć jako "wymiar ziemi". Słowo "ziemia" pojawia się nie jako planeta - część układu słonecznego, ale jako płaszczyzna. Oznakowanie obszarów dla rolnictwa jest najprawdopodobniej początkową podstawą nauki o kształtach geometrycznych, ich typach i właściwościach.

Trójkąt jest najprostszą przestrzenną postacią planimetrii, zawierającą tylko trzy punkty - wierzchołki (nie może być ich mniej). Podstawą fundamentów może być dlaczego pojawia się w nim coś tajemniczego i starożytnego. Wszechstronne oko w trójkącie jest jednym z pierwszych znanych znaków okultystycznych, a geografia jego rozkładu i ram czasowych jest po prostu niesamowita. Od starożytnych egipskich, sumeryjskich, azteckich i innych cywilizacji do bardziej współczesnych społeczności zaklętych okultystów, rozsianych po całym świecie.

Jakie są trójkąty

Regularny wszechstronny trójkąt jest zamkniętą figurą geometryczną składającą się z trzech segmentów o różnych długościach i trzech kątach, z których żaden nie jest prawidłowy. Oprócz tego istnieje kilka specjalnych typów.

Ostry trójkąt ma wszystkie kąty poniżej 90 stopni. Innymi słowy - wszystkie kąty takiego trójkąta są ostre.

Trójkąt prostokątny Nad którym dzieci płakały przez cały czas z powodu obfitości twierdzeń, ma jeden kąt o wielkości 90 stopni lub, jak to się nazywa, także linię prostą.

Rozwarty trójkąt wyróżnia się tym, że jeden z jego narożników jest tępy, czyli jego wielkość jest większa niż 90 stopni.

Trójkąt równoboczny ma trzy boki tej samej długości. Taka postać ma również wszystkie kąty.

Wreszcie, w trójkącie równoramiennym z trzech stron, te dwa są równe.

Cechy wyróżniające

Własności trójkąta równoramiennego również określają jego główną, główną różnicę - równość obu stron. Te boki równe sobie są nazywane udami (lub częściej bocznymi bokami), ale trzecia strona nazywana jest "fundamentem".

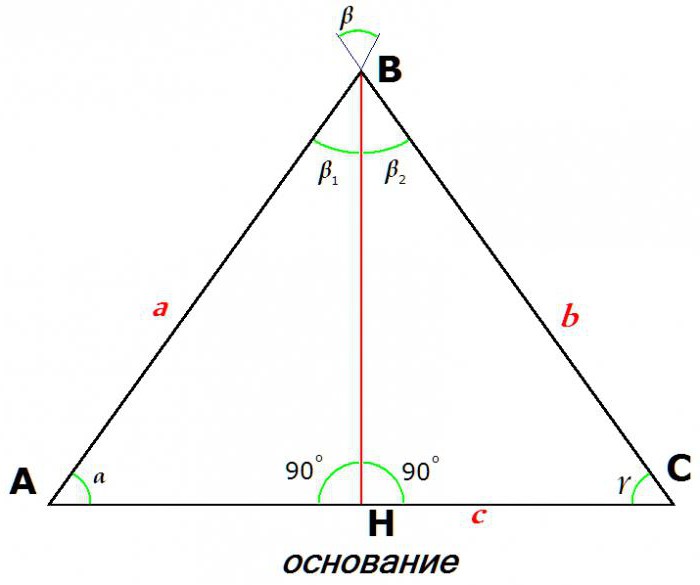
Na tej figurze a = b.

Drugi znak trójkąta równoramiennego wynika z twierdzenia o sinusoidzie. Ponieważ boki a i b są równe, sinusy o przeciwnych kątach są równe:

a / sin γ = b / sin α, skąd mamy: sin γ = sin α.

Równość sinusów oznacza równość kątów: γ = α.

Drugi znak trójkąta równoramiennego to równość dwóch kątów sąsiadujących z podstawą.

Trzeci znak. Trójkąt wyróżnia takie elementy, jak wysokość, dwusieczna i mediana.

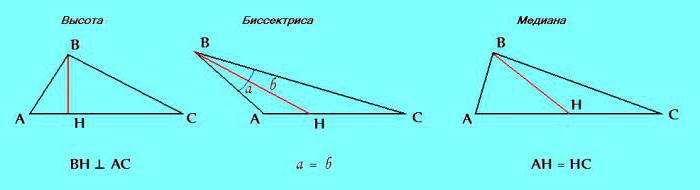
Jeśli w trakcie rozwiązywania problemu okazuje się, że w rozważanym trójkącie dwa dowolne z tych elementów są takie same: wysokość z dwusieczna; dwusieczna z mediana; mediana z wysokością - zdecydowanie można wywnioskować, że trójkąt jest równoramienny.

Geometryczne właściwości rysunku

1. Właściwości trójkąta równoramiennego. Jedną z wyróżniających cech figury jest równość kątów sąsiadujących z podstawą:

α = γ;

<YOU = <BCA.

2. Inna właściwość omówiona powyżej: mediana, dwusieczna i wysokość w trójkącie równoramiennym pokrywają się, jeśli są zbudowane od wierzchołka do podstawy.

3. Równość dwusiecznych narysowanych z wierzchołków u podstawy:

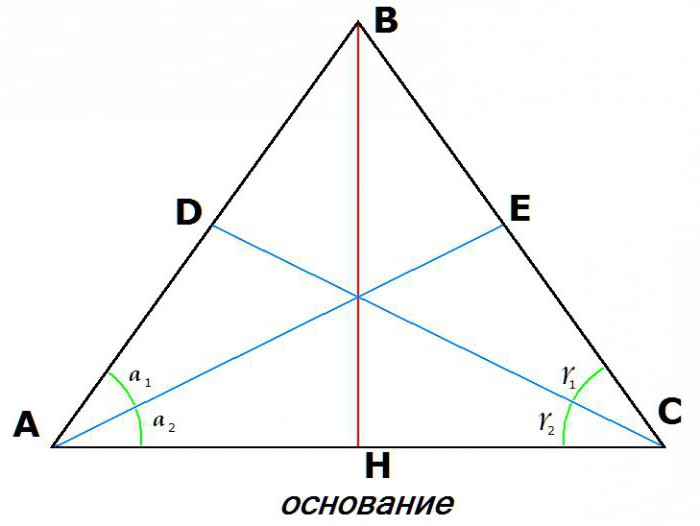
Jeśli AE jest dwusieczną kąta YOU, a CD jest dwusieczną kąta BCA, to: AE = DC.

4. Właściwości trójkąta równoramiennego również zapewniają równość wysokości, które są rysowane od wierzchołków u podstawy.

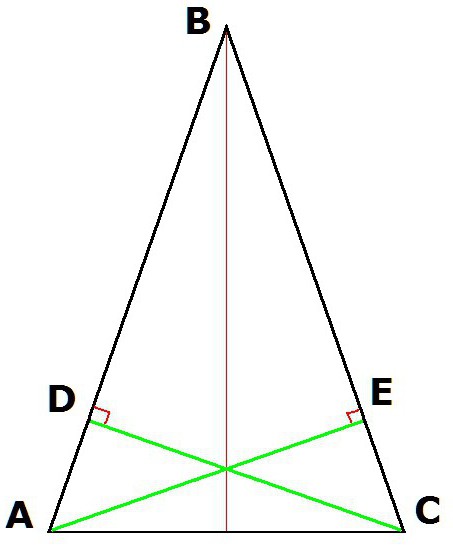
Jeśli skonstruujemy wysokości trójkąta ABC (gdzie AB = BC) z wierzchołków A i C, to wynikowe segmenty CD i AE będą równe.

5. Mediany z narożników u podstawy będą równe.

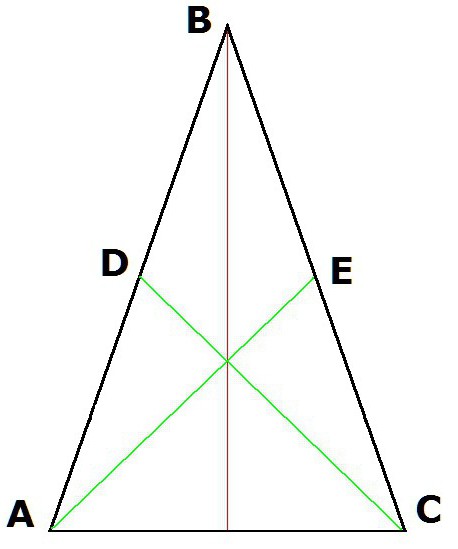
Tak więc, jeśli AE i DC są medianami, to znaczy AD = DB, i BE = EC, następnie AE = DC.

Wysokość trójkąta równoramiennego

Równość boków i kątów w nich dodaje pewne osobliwości do obliczania długości elementów rozpatrywanej figury.

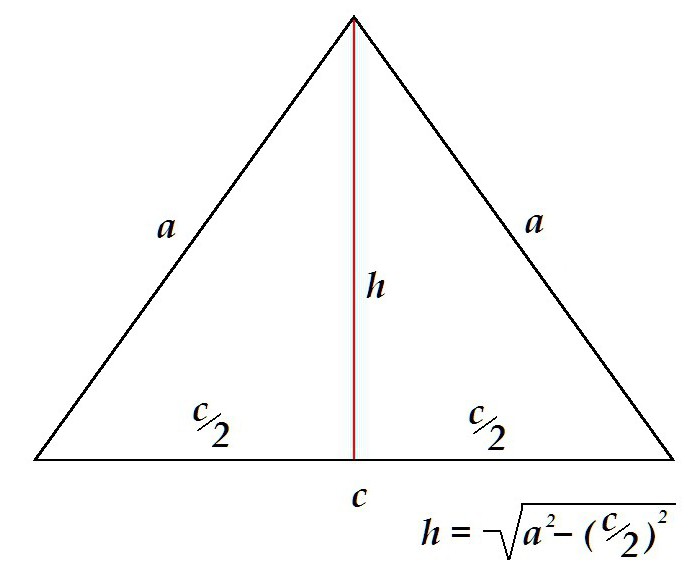
Wysokość w trójkącie równoramiennym dzieli figurę na 2 symetryczne trójkąty prostokątne z przeciwprostokątnymi, w których boki projektują. Wysokość w tym przypadku jest określona przez twierdzenie Pitagorasa jako noga.

Trójkąt może mieć wszystkie trzy strony równe, wtedy będzie nazywał się równoboczny. Wysokość w trójkącie równobocznym jest określana w ten sam sposób, tylko dla obliczeń wystarczy znać tylko jedną wartość - długość boku tego trójkąta.

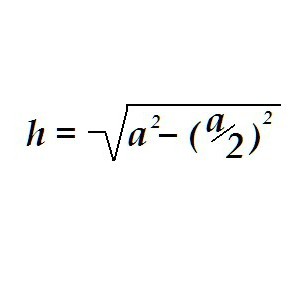
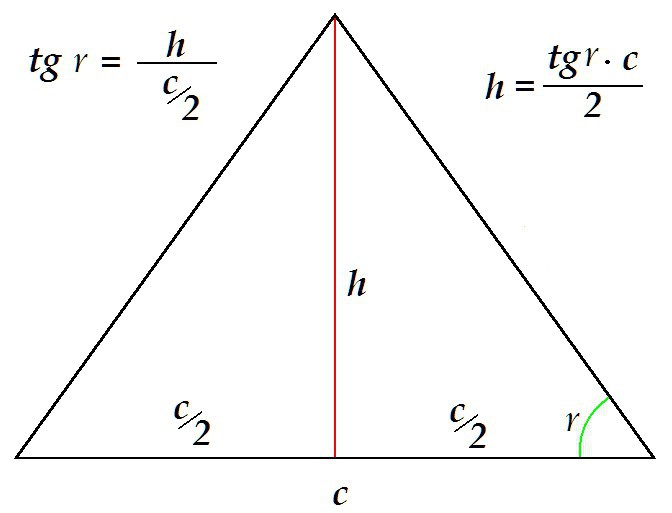
Możliwe jest określenie wysokości w inny sposób, na przykład znajomość podstawy i kąta sąsiadującego z nią.

Mediana trójkąta równoramiennego

Rozważany typ trójkąta, ze względu na jego cechy geometryczne, jest rozwiązany po prostu przez minimalny zestaw danych źródłowych. Ponieważ mediana w trójkącie równoramiennym jest równa zarówno jego wysokości, jak i jej dwusiecznej, algorytm wyznaczania go nie różni się od kolejności, w jakiej te elementy są obliczane.

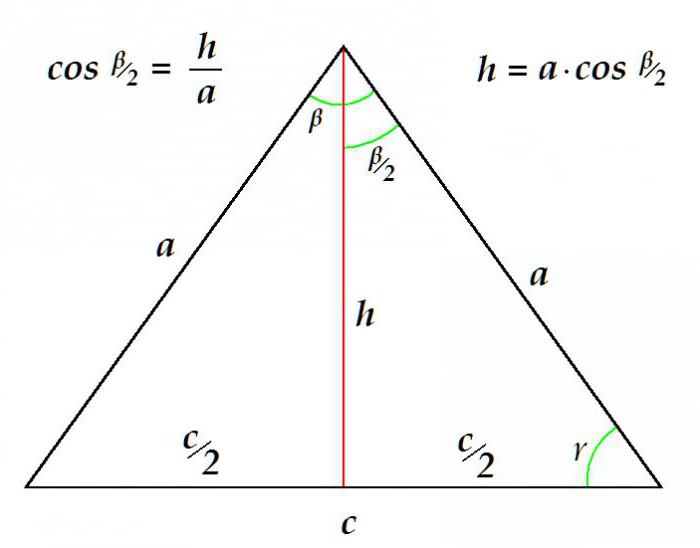
Na przykład można określić długość mediany po znanej stronie i kącie w wierzchołku.

Jak określić obwód

Ponieważ na rozpatrywanym rysunku planimetrycznym obydwa boki są zawsze równe, wówczas w celu określenia obwodu wystarczy znać długość podstawy i długość jednego z boków.

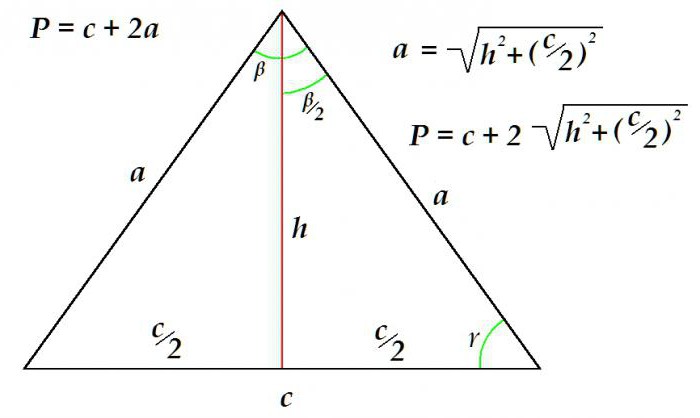
Zastanówmy się, kiedy zdefiniować obwód trójkąta przez znaną podstawę i wysokość.

Obwód jest równy sumie podstawy i podwójnej długości boku. Strona z kolei jest określana za pomocą twierdzenia Pitagorasa jako przeciwprostokątnej trójkąta prostokątnego. Jego długość jest równa pierwiastek kwadratowy sumy kwadratu wysokości i kwadratu połowy podstawy.

Obszar trójkąta równoramiennego

Z reguły występują trudności i obliczenia obszaru trójkąta równoramiennego. W naszym przypadku oczywiście obowiązuje uniwersalna zasada określania obszaru trójkąta jako połowy iloczynu bazy do jej wysokości. Jednak właściwości trójkąta równoramiennego ułatwiają zadanie.

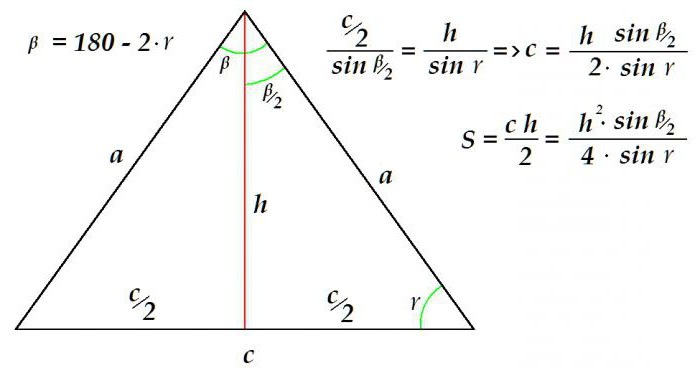
Załóżmy, że wysokość i kąt sąsiadujące z podstawą są znane. Konieczne jest określenie obszaru rysunku. Można to zrobić w ten sposób.

Ponieważ suma kątów każdego trójkąta wynosi 180 °, łatwo jest określić kąt. Ponadto, przy użyciu proporcji sporządzonej zgodnie z twierdzeniem sinusoidy, określa się długość podstawy trójkąta. Wszystko, podstawa i wysokość - wystarczające dane do określenia obszaru - są dostępne.

Inne właściwości trójkąta równoramiennego

Położenie środka okręgu opisanego wokół trójkąta równoramiennego zależy od kąta wierzchołka. Tak więc, jeśli trójkąt równoramienny jest ostry, środek okręgu znajduje się wewnątrz figury.

Środek koła, który jest opisany wokół trójkąta równobocznego, leży na zewnątrz niego. I wreszcie, jeśli kąt na wierzchołku wynosi 90 °, środek leży dokładnie pośrodku podstawy, a średnica okręgu przechodzi przez samą podstawę.

Aby wyznaczyć promień okręgu opisanego wokół trójkąta równoramiennego, wystarczy podzielić długość boku przez podwójną cosinus o połowie kąta w wierzchołku.