Zjawisko załamania światła. Kąty załamania i spadku. Pozorna głębokość zbiornika
Zjawisko załamania światła jest efektem wizualnym, który występuje, gdy wiązka światła przechodzi przez interfejs pomiędzy dwoma mediami, które są dla niej przezroczyste. Ważnymi cechami tego efektu są współczynniki załamania i kąty padania i załamania. W artykule bardziej szczegółowo omawiamy to zjawisko optyczne.
Prawo Snell'a dla zjawiska załamania
Jak wiadomo, każda fala, w tym elektromagnetyczna, rozprzestrzenia się w linii prostej i ze stałą prędkością w jednorodnym materiale. Jak tylko nastąpi naruszenie jednorodności tego materiału, fala zmienia swoją prostoliniową trajektorię. Żywym przykładem takiej zmiany jest załamanie światła.
Załamanie wiązki następuje w zlokalizowanym punkcie w przestrzeni, który znajduje się na styku dwóch przezroczystych mediów o różnych fizycznych właściwościach. Na przykład te środowiska mogą być szkłem, powietrzem, wodą, przezroczystym plastikiem i innymi. Kiedy trafi na drugie medium, światło odchyla się o pewien kąt od pierwotnej trajektorii.
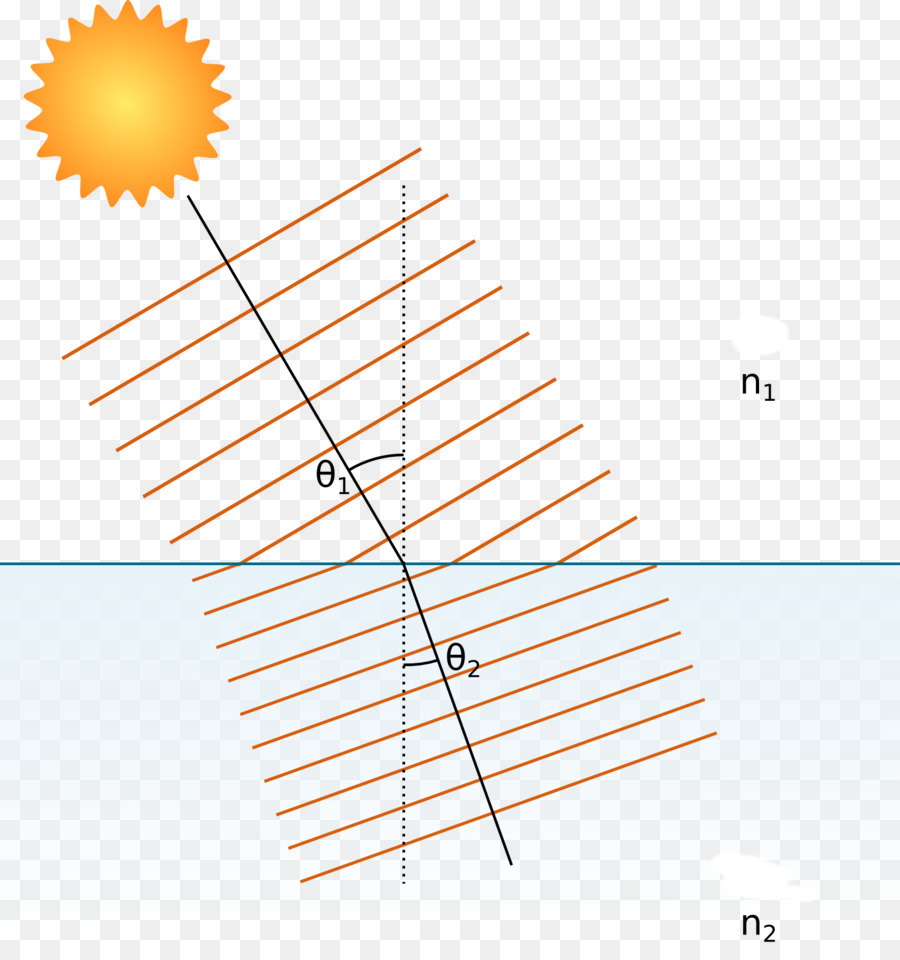
Jeśli mentalnie narysujesz prostopadle przez punkt, w którym promień przecina płaszczyznę rozdzielania mediów i wyznacza kąt między prostopadłym a promieniem jako θ 1 , a kąt między tą samą prostopadłą a promieniem, która przechodzi do drugiego medium, jako θ 2 , wówczas następująca relacja utrzymuje:
sin (θ 1 ) * n 1 = sin (θ 2 ) * n 2
Kąty teta jeden (θ 1 ) i theta dwa (θ 2 ) nazywane są odpowiednio kątami padania i załamania. Wartości n 1 , n 2 są ważnymi cechami optycznymi pierwszego i drugiego nośnika, nazywane są współczynnikami załamania światła.
Powyższy wzór nazywa się prawem Snella (Snellius), ponieważ holenderski naukowiec Willebrord Snellus na początku XVII wieku sformułował go po raz pierwszy w swojej nowoczesnej formie, analizując dużą ilość materiału doświadczalnego.

Współczynnik załamania światła
Zgodnie z matematyczną definicją tej wielkości fizycznej jest ona równa stosunkowi dwóch prędkości światła: w próżni i w materiale, czyli:
n = c / v
Ponieważ c> v, wtedy n zawsze będzie większe niż jeden.
Współczynnik załamania światła ma różne wartości dla różnych substancji. Na przykład dla powietrza jest prawie równa 1, a dla wody 1,33. Wartość n zależy również od składu chemicznego tego samego materiału. Na przykład wskaźnik refrakcji szkła zależy od jego rodzaju i wynosi od 1,5 do 1,66.
Oprócz właściwości materiału, n zmienia się znacznie, jeśli zmienisz częstotliwość światła w wiązce. Kąt załamania światła niebieskiego jest zawsze większy niż czerwony. Liczby podane w poprzednim akapicie odnoszą się do żółtej części widma widocznej przez człowieka (λ ≈ 590 nm).
Gęstość optyczna ośrodka
Ta fizyczna cecha określa, jak mocno medium spowalnia prędkość światła. Gęstość optyczna jest jednoznacznie określona przez współczynnik załamania światła. Na przykład woda jest optycznie bardziej gęsta niż powietrze, a każdy rodzaj szkła jest bardziej gęsty niż woda.
Jeśli spojrzeć na formułę Snell, widać, że im większa gęstość optyczna medium, tym niższy kąt do normalnego będzie to światło. Ten wniosek jest ważny bez względu na to, z jakiego medium i na jakie światło padnie wiązka. Zatem biorąc pod uwagę granicę woda-powietrze, kąt załamania światła będzie mniejszy niż kąt padania, gdy wiązka przesunie się do wody. Jeśli zmienisz kierunek wiązki, kąt padania będzie mniejszy.
Wyzwanie stosowania prawa Snell'a
Wiadomo, że promień światła pada na powierzchnię wody pod kątem 32 °. Konieczne jest określenie kąta załamania światła, a także wielkości jego zmiany, jeśli zwiększy się kąt padania o 10 o .
Ilość refrakcji światła można określić na podstawie prawa Snella. Mamy:
θ 2 = arcsin (sin (θ 1 ) * n 1 / n 2 )
Ponieważ światło pada z powietrza do wody, to n 1 = 1, a n 2 = 1,33. Wiedząc, że = 1 = 32 o , otrzymujemy:
θ 2 = arcsin (sin (32 o ) * 1 / 1.33) = 23,48 o
Jak widać, kąt znacznie się zmniejszył. Teraz obliczamy kąt załamania wiązki, jeśli θ 1 = 42 o . Korzystając z tej samej formuły, otrzymujemy:
θ 2 = arcsin (sin (42 o ) * 1 / 1.33) = 30,21 o
Zmierz różnicę między uzyskanymi kątami, otrzymamy:
30,21 o - 23,48 o = 6,73 o
Uzyskany wynik oznacza, że zmiany między kątami padania i załamania nie są liniowe. Wzrost kąta padania o 10 ° prowadził do zmiany kąta załamania tylko o 6,7 o .
Zadanie określania widocznej głębokości

Wiele osób zauważyło, że patrząc na dno zbiornika, kamienie leżące na nim i rosnące glony zdają się zbliżać do powierzchni. Oblicz, stosując prawo załamania, ponieważ rzeczywiste i pozorne głębokości różnią się od siebie. W tym celu rozważymy małe kąty padania, czyli obserwator spogląda pionowo w dół do dna zbiornika. Poniżej znajduje się odpowiednia liczba.
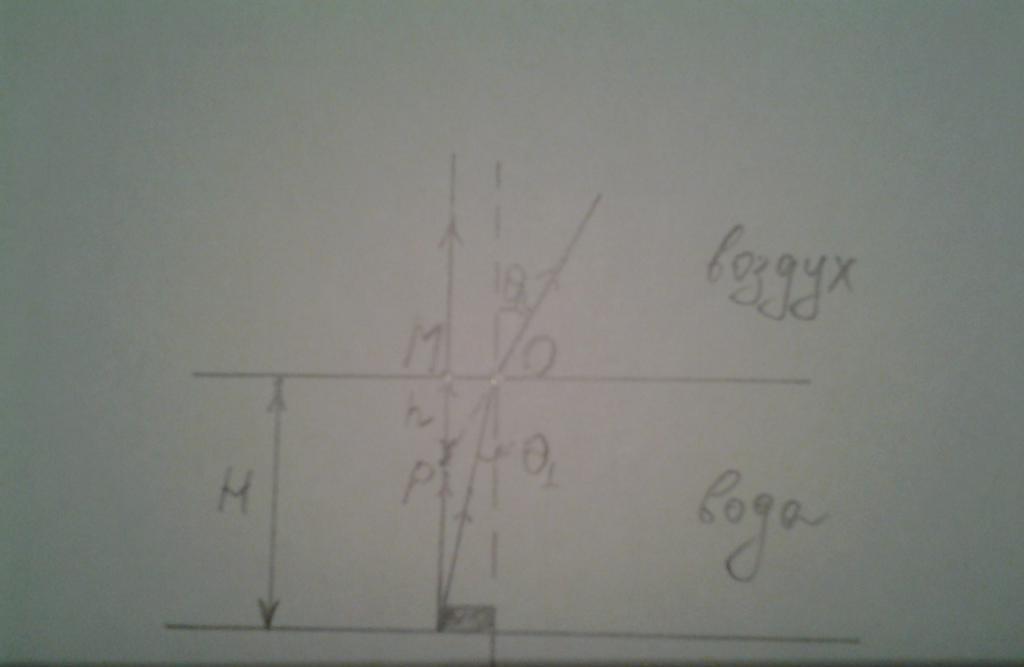
Rysunek pokazuje obiekt leżący na dole. Ponieważ dwie wiązki, które wychodzą z tego samego punktu obiektu, przecinają się w punkcie P dla obserwatora, głębokość h = MP będzie widoczna.
Aby znaleźć h, zastanów się w prawym trójkącie POM. Przedział MO to H * tg (θ 1 ), kąt POM wynosi 90 - θ2. Teraz możesz napisać:
tg (90-θ 2 ) = h / (H * tg (θ 1 ))
Wiedząc, że styczna jest równa stosunkowi sinusoidy do cosinusa, i używając formuł dla funkcji trygonometrycznych, możemy przepisać tę równość w następujący sposób:
cos (θ 2 ) / sin (θ 2 ) = cos (θ 1 ) * h / (H * sin (θ 1 ))
Biorąc pod uwagę małe kąty (blisko pionu), cosinusy będą prawie równe jednostkom, więc ostatnia formuła zostanie uproszczona do postaci:
h = h * sin (θ 1 ) / sin (θ 2 )
Ale stosunek sinusoidy jest równy odwrotnemu stosunkowi współczynników załamania mediów zgodnie z prawem Snell'a, dlatego zapisujemy:
h = H * n 2 / n 1
Gdy wiązka wysuwa się z wody, n 2 jest wskaźnikiem dla powietrza, który jest równy jeden. Ostateczna formuła dla pozornej głębokości zbiornika podczas oglądania w pionie to:
h = h / n, gdzie n = 1,33
Zatem widoczna głębokość jest o około 25% mniejsza od rzeczywistej.