Ruch translacyjny: definicja, formuły, twierdzenie
Mechanika uwzględnia wszystkie możliwe ruchy punktu materialnego i ciała stałego. Wszystkie są opisane w kilku sekcjach. Na przykład pytanie, jak się poruszą, będzie prerogatywą kinematyki. Opisuje szczegółowo ruch translacyjny, a także bardziej złożony - rotacyjny. Po pierwsze, to jest łatwiejsze. Ponieważ bez tego trudno jest przejść do następujących tematów.
Jakie założenia pozwalają mechanicy?
W wielu problemach dopuszcza się przybliżenie. Wynika to z faktu, że nie wpłynie to na wynik, ale uprości to proces rozumowania.
Pierwsze przybliżenie jest związane z rozmiarem ciała. Jeśli rozpatrywane ciało jest znacznie mniejsze niż pozostałe w tym samym układzie odniesienia, wówczas jego wymiary są pomijane. A ciało samo w sobie staje się materialnym punktem.
Drugi wynika z braku deformacji ciała podczas jego ruchu. Lub nawet tak mało znaczący jego rozmiar, który może być całkowicie zaniedbany.

Jaki jest ruch translacyjny ciała?
W celu wyjaśnienia, musisz wziąć pod uwagę dowolne dwa punkty wewnątrz bryły. Muszą połączyć segment. Jeśli ten segment pozostaje równoległy do początkowej pozycji podczas ruchu, wówczas mówi się, że jest to ruch do przodu.
Jeśli istnieje zaniedbanie wielkości ciała i jest brane pod uwagę punkt materialny Ten segment jest nieobecny i porusza się wzdłuż linii.
Żywe przykłady takiego ruchu
Pierwszą rzeczą do zapamiętania jest samochód windy. Doskonale ilustruje ruch do przodu ciała. Winda zawsze porusza się ściśle w górę lub w dół bez żadnego obrotu.
Poniższy przykład ilustrujący ruch translacyjny to ruch kabiny diabelskiego koła. Jest to jednak realne tylko w sytuacji, gdy niewielkie nachylenie kabiny na początku każdego przesunięcia nie jest brane pod uwagę.
Trzecia sytuacja, kiedy można mówić o ruchu do przodu, wiąże się z ruchem pedałów rowerowych. Ich ruch jest rozpatrywany w stosunku do ramy. Tutaj znowu zakłada się założenie, że stopy osoby nie huśtają się podczas jazdy.
Listę można uzupełnić przesuwając tłoki, które oscylują wewnątrz cylindrów silnika spalinowego.

Główne pojęcia
Kinematyka ruchu translacyjnego polega na badaniu i opisywaniu ruchu ciał stałych i punktów materialnych. Jednak nie bierze pod uwagę powodów, które zmuszają ciało do tego. Aby opisać ruch, współrzędne będą wymagane do wskazania jego położenia w przestrzeni. Ponadto znajomość prędkości jest wymagana, w dowolnym czasie.
Po pierwsze, warto zapamiętać trajektorię. Jest to linia, wzdłuż której poruszało się ciało.
Pierwszym jest wejście w ruch. Jest to wektor oznaczony łacińską literą r. Może łączyć pochodzenie z pozycją punktu materialnego. W innych przypadkach wektor ten jest pobierany od początkowego do końcowego punktu trajektorii. Jednostkami przemieszczenia są metry.
Drugą wartością zasługującą na uwagę jest sposób. Jest równa długości trajektorii wzdłuż ciała. Ścieżka jest oznaczona literą alfabet łaciński S, który jest również mierzony w metrach.

Podstawowe formuły
Teraz nadszedł czas, aby przyspieszyć. Jest także wektorem. Co więcej, charakteryzuje nie tylko kierunek ruchu ciała, ale także szybkość jego ruchu. Wektor prędkości jest zawsze kierowany wzdłuż linii stycznej, którą można narysować do dowolnego punktu trajektorii. Jest to oznaczone literą V. Jednostkami jego pomiaru są m / s.
Szybkość w każdej chwili ruchu można zdefiniować jako pochodną ruchu w czasie. Jeśli chodzi o problem jednolity ruch, następnie obowiązuje następująca formuła:
- V = S: t, gdzie t jest czasem ruchu.
W sytuacji, gdy zmienia się kierunek ruchu, musisz użyć sumy wszystkich ruchów.
Kolejną wartością jest przyspieszenie. Ponownie, wielkość wektora, która jest skierowana w kierunku prędkości o dużej wartości. Jest zdefiniowany jako pierwsza pochodna prędkości w czasie. Przyjęte oznaczenie - litera "a". Wymiar jest wskazany wm / s 2 .
Formuły dla każdego komponentu przyspieszenia, kierowane wzdłuż osi, są obliczane jako stosunek zmiany prędkości wzdłuż tej osi do przedziału czasu. Jeśli utworzysz zapis matematyczny, otrzymasz następujące informacje:
- i x = ΔV x : Δt.
Dla rzutów przyspieszenia na inne osie, wzory są podobne.
Ponadto, rozważając ruch wzdłuż trajektorii z zakrętami, możliwe jest rozłożenie wektora przyspieszenia na dwa terminy:
- a = a t + a n , gdzie t jest przyspieszeniem stycznym skierowanym wzdłuż stycznej gięcia, a n jest normalne, co wskazuje na środek krzywizny.
Ruch translacyjny dowolnego ciała stałego jest zredukowany do opisu ruchu tylko jednego z jego punktów. Formuły do zastosowania to:
- S = S 0 + V 0 t + (przy 2 ): 2.
- V = V 0 + at.
W tym wzorze indeksy "zero" oznaczają początkowe wartości ilości.
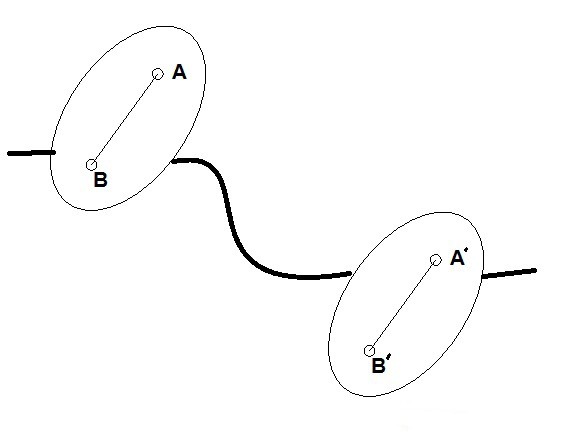
Twierdzenie o wielkiej translacji
Jego sformułowanie jest następujące: trajektoria, prędkość i przyspieszenie wszystkich punktów ciała są takie same podczas ruchu do przodu.
Aby to udowodnić, musisz napisać formułę dodatki wektorowe przemieszczanie i wektor łączący dwa dowolne punkty. Trajektorie wszystkich punktów są uzyskiwane z powodu ich przeniesienia wzdłuż drugiego wektora. I z czasem nie zmienia swojego kierunku i wielkości. Dlatego można argumentować, że wszystkie punkty ciała poruszają się po tych samych trajektoriach.
Jeśli przyjmiemy pochodną czasu, otrzymamy wartość prędkości. Co więcej, wyrażenie jest uproszczone w takim stopniu, że prędkości dwóch punktów są równe.
Pole pochodnej drugiego czasu jest wynikiem równości przyspieszeń dwóch punktów.