Mediana trójkąta: Formuła i właściwości

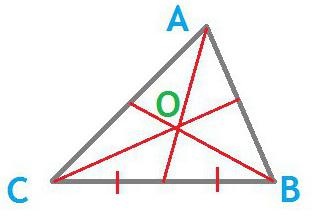
Mediana to odcinek narysowany od wierzchołka trójkąta do środka przeciwległej strony, czyli dzieli go przez punkt przecięcia na pół. Punkt, w którym mediana przecina przeciwny wierzchołek, z którego się wydostaje, bok, nazywany jest podstawą. Każda mediana trójkąta przechodzi przez jeden punkt zwany punktem przecięcia. Jego formuła długości może być wyrażona na kilka sposobów.

Formuły wyrażania średniej długości

• Często w problemach z geometrią studenci mają do czynienia z takim segmentem, jak mediana trójkąta. Wzór jego długości wyrażony jest przez boki:

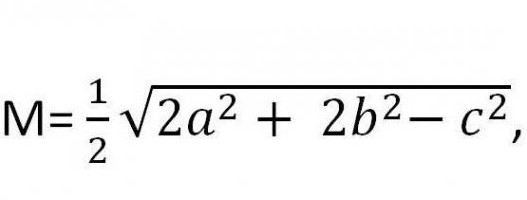
gdzie a, b i c są bokami. I z tym jest strona, do której spada mediana. To najprostsza formuła. Mediany z trójkąta są czasami wymagane do obliczeń pomocniczych. Istnieją inne formuły.

• Jeżeli obliczenia są znane z dwóch boków trójkąta i pewnego kąta α między nimi, wówczas długość mediany trójkąta, która spadła na trzecią stronę, będzie wyrażona następująco.

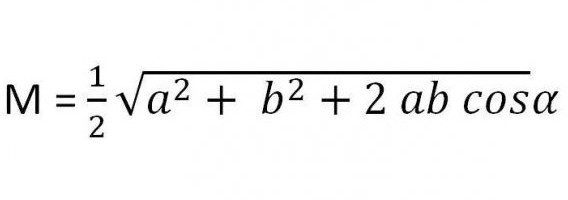
Podstawowe właściwości

• Wszystkie mediany mają jeden wspólny punkt przecięcia O i są dzielone przez dwa do jednego, jeśli liczymy od góry. Punkt ten nazywany jest środkiem ciężkości trójkąta.
• Mediana dzieli trójkąt na dwa inne, których obszary są równe. Takie trójkąty są nazywane równymi.
• Jeśli utrzymasz wszystkie mediany, trójkąt zostanie podzielony na 6 figur o równych wymiarach, które będą również trójkątami.
• Jeśli wszystkie trzy boki są równe w trójkącie, to każda z nich będzie również wysokością i dwusieczną, to znaczy prostopadłą do strony, na którą jest narysowana, i dzieli kąt, z którego wychodzi.
• W trójkącie równoramiennym mediana, pomijana z wierzchołka, która jest przeciwna do strony, która nie jest równa żadnej innej, będzie również wysokością i dwusieczną. Mediany pominięte w innych wierzchołkach są równe. Jest to również niezbędny i wystarczający warunek dla równoramiennych.
• Jeśli trójkąt jest podstawą zwykłej piramidy, wysokość obniżona na tej podstawie jest rzutowana w punkcie przecięcia wszystkich median.

• W trójkąt prostokątny mediana przyciągnięta do największego boku jest o połowę mniejsza.
• Niech O będzie punktem przecięcia się środkowej części trójkąta. Poniższy wzór będzie prawdziwy dla dowolnego punktu M.

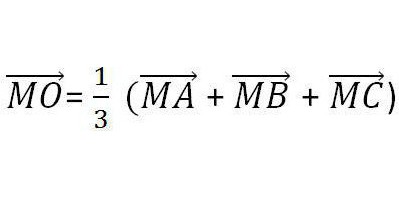
• Inna właściwość ma medianę trójkąta. Wzór kwadratu jego długości poprzez kwadraty boków przedstawiono poniżej.

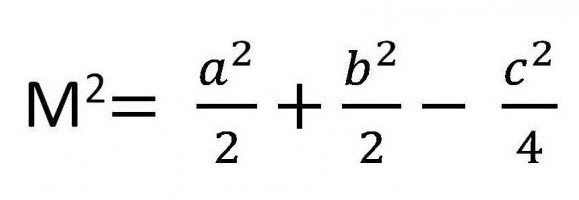
Właściwości stron, w których odbywa się mediana

• Jeśli połączysz dwa punkty przecięcia się środkowych z bokami, do których są obniżone, wynikowy segment będzie środkową linią trójkąta i będzie jedną sekundą od strony trójkąta, z którym nie ma wspólnych punktów.
• Podstawy wysokości i median w trójkącie, a także punkty środkowe segmentów łączących wierzchołki trójkąta z punktem przecięcia wysokości, leżą na tym samym okręgu.

Podsumowując, logiczne jest stwierdzenie, że jednym z najważniejszych segmentów jest mediana trójkąta. Jego wzór może być użyty przy ustalaniu długości jego drugich boków.