Wektor. Czym jest wektor?

Taka koncepcja, jak wektor, rozpatrywana jest w niemal wszystkich naukach przyrodniczych i może mieć zupełnie inne znaczenie, dlatego niemożliwe jest podanie unikalnej definicji wektora dla wszystkich obszarów. Ale spróbujmy to rozgryźć. Czym więc jest wektor?

Pojęcie wektora w klasycznej geometrii

Wektor w geometrii to segment, dla którego wskazuje się, który z jego punktów jest początkiem, a który jest końcem. To znaczy, mówiąc prościej, wektor jest ukierunkowanym segmentem.

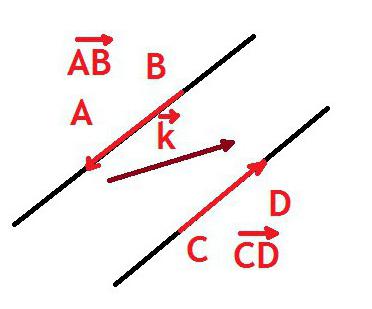
W związku z tym wektor oznaczono (co jest brane pod uwagę powyżej), a także segment, to znaczy dwa wielkimi literami Alfabet łaciński z kreską lub strzałką skierowaną w prawo z góry. Możesz go również podpisać małą (małą) literą alfabetu łacińskiego za pomocą myślnika lub strzałki. Strzałka jest zawsze skierowana w prawo i nie zmienia się w zależności od położenia wektora.

Zatem wektor ma kierunek i długość.

Oznaczenie wektora zawiera jego kierunek. Jest to wyrażone jak na poniższym rysunku.

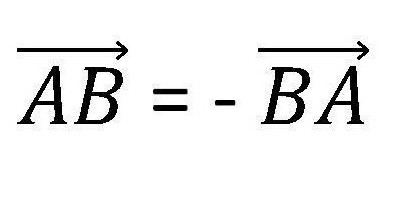
Zmiana kierunku zmienia wartość wektora na przeciwny.

Długość wektora jest długością odcinka, z którego jest utworzony. Jest oznaczony jako moduł wektora. Zostało to pokazane na poniższym rysunku.

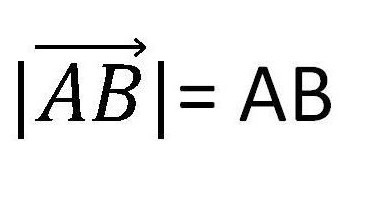
Odpowiednio, zero jest wektorem, którego długość wynosi zero. Wynika z tego, że wektor zerowy jest punktem, a punkty początkowe i końcowe pokrywają się w nim.

Długość wektora - wartość nie zawsze jest ujemna. Innymi słowy, jeśli istnieje segment, to koniecznie ma on określoną długość lub jest punktem, wtedy jego długość jest równa zeru.

Pojęcie punktu jest podstawowe i nie ma definicji.

Wektor dodatek

Istnieją specjalne formuły i reguły dla wektorów, które możesz dodać.

Reguła trójkąta. Dla dodatki wektorowe zgodnie z tą zasadą wystarczy połączyć koniec pierwszego wektora i początek drugiego, używając translacji równoległej i połączyć je. Wynikowy trzeci wektor będzie równy dodaniu dwóch pozostałych.

Reguła równoległoboku. Aby dodać zgodnie z tą zasadą, konieczne jest narysowanie obu wektorów z jednego punktu, a następnie narysowanie innego wektora od końca każdego z nich. To znaczy, drugi zostanie narysowany z pierwszego wektora, a pierwszy z drugiego. Wynikiem jest nowy punkt przecięcia i powstaje równoległobok. Jeśli połączymy punkt przecięcia początków i końców wektorów, wynikowy wektor będzie wynikiem dodania.

Podobnie można wykonywać i odejmować.

Różnica wektorowa

Podobnie do dodawania wektorów, można je odjąć. Opiera się na zasadzie przedstawionej na poniższym rysunku.

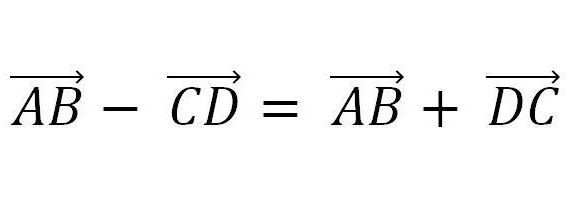
Oznacza to, że wystarczy odjąć wektor w postaci wektora, przeciwnie do niego i obliczyć według zasad dodawania.

Również absolutnie dowolny niezerowy wektor może być pomnożony przez dowolną liczbę k, to zmieni jego długość k razy.

Oprócz nich istnieją inne formuły wektorów (na przykład, aby wyrazić długość wektora poprzez jego współrzędne).

Lokalizacja wektorów

Z pewnością wielu zetknęło się z takim pojęciem, jak wektor kolinearny. Czym jest kolinearność?

Kolinearność wektorów jest odpowiednikiem linii równoległych. Jeśli dwa wektory leżą na liniach prostych, które są równoległe do siebie lub na jednej linii prostej, wówczas takie wektory są nazywane współliniowymi.

Kierunek W stosunku do siebie, wektory współliniowe mogą być współkierowane lub skierowane przeciwnie, jest to określane przez kierunek wektorów. Odpowiednio, jeśli wektor jest współkierowany z innym, to wektor przeciwny do niego jest skierowany przeciwnie.

Pierwsza figura pokazuje dwa przeciwnie skierowane wektory, a trzeci, który nie jest dla nich współliniowy.

Po wprowadzeniu powyższych właściwości możliwe jest podanie definicji i wektorów równych - są to wektory, które są skierowane w tym samym kierunku i mają tę samą długość segmentów, z których są utworzone.

W wielu naukach stosowana jest również koncepcja wektora promienia. Taki wektor opisuje pozycję jednego punktu płaszczyzny względem innego ustalonego punktu (często jest to pochodzenie).

Wektory w fizyce

Załóżmy, że przy rozwiązywaniu problemu pojawił się stan: ciało porusza się z prędkością 3 m / s. Oznacza to, że ciało porusza się w określonym kierunku w jednej linii prostej, więc ta zmienna będzie wartością wektorową. W przypadku rozwiązania ważne jest, aby znać zarówno wartość, jak i kierunek, ponieważ w zależności od rozważań prędkość może być równa 3 m / s i -3 m / s.

Ogólnie rzecz biorąc, wektor w fizyce służy do wskazywania kierunku siły działającej na ciało i do określania wypadkowej.

Kiedy te siły są wskazane na rysunku, są one oznaczone strzałkami z podpisem wektora nad nim. Klasycznie, długość strzały jest równie ważna, za jej pomocą wskazują one, która siła działa silniej, ale ta własność boczna nie jest warta polegania na niej.

Wektor w algebrze liniowej i analizie matematycznej

Elementy przestrzeni liniowych są również nazywane wektorami, ale w tym przypadku są uporządkowanym układem liczb opisującym niektóre elementy. Dlatego kierunek w tym przypadku nie ma już znaczenia. Definicja wektorowa w klasycznej geometrii i w analiza matematyczna różnią się znacznie.

Wektory rzutowania

Projektowany wektor - co to jest?

Dość często, dla prawidłowego i wygodnego obliczenia, konieczne jest rozszerzenie wektora w dwuwymiarowej lub trójwymiarowej przestrzeni wzdłuż osi współrzędnych. Ta operacja jest konieczna, na przykład, w mechanice podczas obliczania sił działających na ciało. Wektor w fizyce jest często używany.

Aby wykonać rzut, wystarczy obniżyć pion prostopadłości od początku i końca wektora na każdą z osi współrzędnych, otrzymane na nich segmenty będą nazywane rzutem wektora na oś.

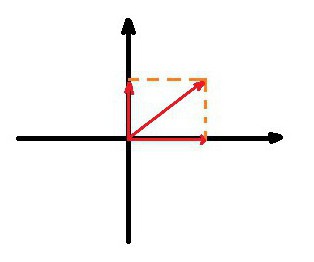
Aby obliczyć długość rzutu, wystarczy pomnożyć jego początkową długość przez pewną funkcję trygonometryczną, która jest uzyskiwana przez rozwiązanie mini-problemu. Zasadniczo jest trójkąt prostokątny w którym przeciwprostokąt jest oryginalnym wektorem, jedna z nóg jest rzutem, a druga jest obniżoną prostopadłą.