Twierdzenie Viety: przykłady jego użycia podczas pracy z równaniami kwadratowymi
Podczas studiowania metod rozwiązywania równań drugiego rzędu w szkolnym kursie algebry należy wziąć pod uwagę właściwości uzyskanych korzeni. Są one obecnie znane jako twierdzenie Viet. Przykłady jego użycia podano w tym artykule.
Równanie kwadratowe
Równanie drugiego rzędu jest równaniem, które pokazano na poniższym zdjęciu.
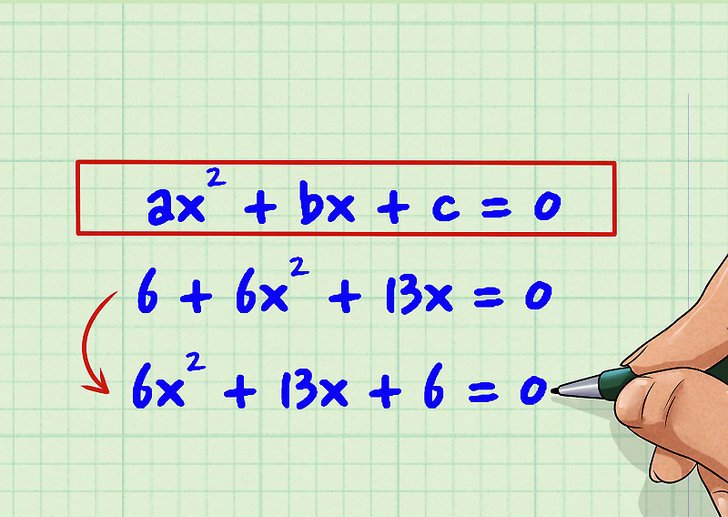
Tutaj symbole a, b, c to niektóre liczby, które nazywane są współczynnikami danego równania. Aby rozwiązać problem równości, należy znaleźć wartości x, które sprawiają, że jest on prawdziwy.
Zauważ, że ponieważ maksymalna wartość stopnia, w którym X jest podniesiona, jest równa dwóm, wtedy liczba korzeni w ogólnym przypadku jest również równa dwóm.
Istnieje kilka sposobów rozwiązania tego rodzaju równości. W tym artykule rozważamy jeden z nich, który dotyczy użycia tak zwanego twierdzenia Wietna.
Formułowanie twierdzenia Viet

Pod koniec XVI wieku słynny matematyk Francois Vietta (Francuz) zauważył, analizując właściwości korzeni różnych równań kwadratowych, że pewne ich kombinacje spełniają określone relacje. W szczególności kombinacje te są ich produktem i sumą.
Twierdzenie Vieta ustala: korzenie równania kwadratowego wraz z ich sumą dają stosunek współczynników liniowych do kwadratowych przyjmowanych ze znakiem przeciwnym, a gdy są wytwarzane, prowadzą do stosunku współczynnika swobodnego do współczynnika kwadratowego.
Jeśli ogólna forma równania jest napisana tak, jak jest przedstawiona na zdjęciu w poprzedniej części artykułu, to matematycznie to twierdzenie można zapisać w postaci dwóch równości:
- r 2 + r 1 = -b / a;
- r 1 x r 2 = c / a.
Gdzie r 1 , r 2 jest wartością pierwiastków danego równania.
Te dwa równania można wykorzystać do rozwiązania wielu bardzo różnych problemów matematycznych. Zastosowanie twierdzenia Viet w przykładach z rozwiązaniem podano w kolejnych częściach artykułu.
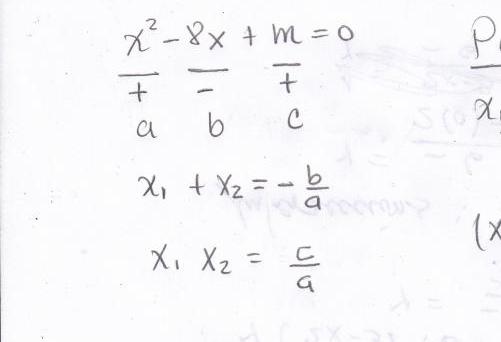
Problem numer 1: przywróć równanie
Przedstawimy następujący problem dotyczący zastosowania twierdzenia Viet. Przykład równania jest podany następująco: -3.4 * x - 3 * s * x 2 + k = 0. Musisz znaleźć wartości s i k, wiedząc, że dwie liczby są rozwiązaniami tego równania: -1,2 i 4.
Najpierw musisz zdecydować o wartości współczynników w tym wyrażeniu. Wynika z tego, że a = -3 * s, b = -3,4 i c = k.
Teraz możesz użyć twierdzenia Viet. Dla sumy korzeni otrzymujemy następującą równość: -1,2 + 4 = - (- 3,4) / (-3 * s), skąd otrzymujemy s = -0,40476 (do obliczenia tego wyrażenia zaleca się użycie kalkulatora). To znaczy, a = -3 * s = 1,21429. Aby wyprodukować korzenie, mamy:
(-1,2) * 4 = k / 1,21429, skąd k = -5,82859.
Zrekonstruowane równanie będzie odpowiadać formie: -3,4 * x + 1,21429 * x 2 - 5,82859 = 0. Aby sprawdzić, czy problem został rozwiązany poprawnie, i czy wystąpił błąd w jego rozwiązaniu, konieczne jest zastąpienie znanych wartości root w przywróconym wyrażeniu. Otrzymujemy: -3,4 * (-1,2) + 1,21429 * (-1,2) 2 - 5,82859 = 0,00001 ≈ 0 i -3,4 * (4) + 1,21429 * ( 4) 2 - 5,82859 = 0,00005 ≈ 0.
Jak widzimy, uzyskane równości są rzeczywiście spełnione. Mały błąd wynika z faktu, że przywracając równanie, zaokrąglono otrzymane liczby do 5 miejsc dziesiętnych.
Problem numer 2: znajdź korzenie równania
Rozwiązanie równań kwadratowych według twierdzenia Viet (patrz przykład poniżej) jest możliwe nie we wszystkich przypadkach. Oznacza to, że ta metoda nie jest uniwersalna, ponieważ jeśli współczynniki równania okażą się "niewygodne", to nie zadziała.
Uniwersalnymi metodami rozwiązywania tego typu ekspresji są użycie dyskryminatora lub dodatku do pełnego kwadratu. Jednak w tym przypadku znaczenie twierdzenia Viet jest takie, że pozwala ono odgadnąć nieznane korzenie bez wykonywania skomplikowanych obliczeń matematycznych.
Na przykład podane jest następujące wyrażenie: -x 2 + 2 * x + 3 = 0. Powinniśmy użyć twierdzenia Vieta, aby znaleźć rozwiązania dla tej równości. Niech jego korzenie będą liczbami r 1 i r 2 . Następnie możesz napisać następujący układ równań:
r 1 + r 2 = -2 / (-1) = 2;
r 1 * r 2 = 3 / (-1) = -3.
Teraz należy zgadnąć, która suma liczb wynosi dwa, a ich produkt będzie wynosił -3. Oczywiście są to liczby 3 i -1. Będą korzeniami równania.
Jeśli trochę zagłębimy się w ten temat, to należy zauważyć, że każde równanie drugiego rzędu, które można łatwo przedstawić jako iloczyn dwóch czynników, można rozwiązać za pomocą rozważanego twierdzenia. Rzeczywiście, w tym przypadku możemy napisać (3-x) * (x + 1), jeśli rozszerzymy nawiasy, otrzymamy oryginalne wyrażenie.
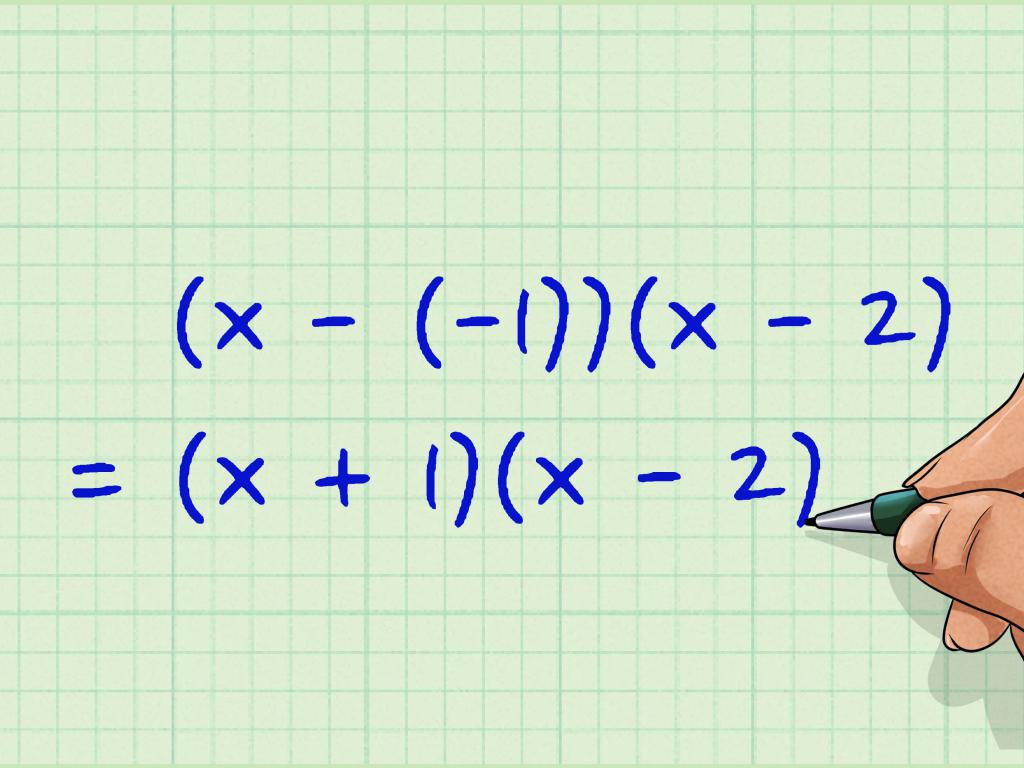
Problem numer 3: suma kwadratów
Podajemy kolejny przykład twierdzenia Viet z rozwiązaniem. Biorąc pod uwagę równanie:
6 * x 2 - 13 * x + 11 = 0. Konieczne jest znalezienie sumy kwadratów jej dwóch korzeni, czyli (r 1 ) 2 + (r 2 ) 2 .
Oczywiście, możesz rozwiązać to równanie na jeden ze sposobów, a następnie odpowiedzieć na pytanie o problem. Jednakże, jeśli przywołamy twierdzenie Wietna i właściwość kwadratu sum, wtedy nie ma takiej potrzeby.
Należy pamiętać, że obliczana jest suma dwóch kwadratów do kwadratu. Następnie stwierdzamy, że aby znaleźć nieznaną sumę kwadratów, konieczne jest obliczenie wartości wyrażenia (r 1 + r 2 ) 2 - 2 * r 1 * r 2 . Korzystamy z obu równości rozpatrywanego twierdzenia, otrzymujemy: (13/6) 2 - 2 * 11/6 = 1,02 (7) (7 w okresie).
W ten sposób, stosując twierdzenie Viet, zaoszczędziliśmy czas na rozwiązaniu równania. Zasadniczo, właściwości korzeni można wykorzystać do wszelkich zadań związanych z obliczaniem ich różnych kombinacji.