Co to jest stożek? Koncepcja i zdjęcie
Stereometria jest ważną częścią geometrii, której przedmiotem badań są właściwości i cechy figur w przestrzeni trójwymiarowej. W tym artykule rozważymy jedną z takich wielkości wolumetrycznych. Zapoznajmy się z pytaniem, co to jest stożek.
Stożek postać
Podajemy najbardziej ogólną definicję stożka. Pod tym rysunkiem rozumiemy powierzchnię, która powstaje w wyniku połączenia prostych odcinków pewnego punktu w przestrzeni ze wszystkimi punktami danej krzywej. W tym przypadku określony punkt w przestrzeni nie powinien znajdować się w płaszczyźnie krzywej. Na przykład, jeśli krzywa ma kształt paraboli, wówczas figura uzyskana za pomocą opisanej metody zostanie nazwana stożkiem parabolicznym, jeśli krzywa jest elipsą, stożek będzie eliptyczny i tak dalej.
Po podaniu geometrycznej definicji tego, czym jest stożek, prezentujemy zdjęcie, które pokazuje wizualnie możliwe formy tej figury.

Patrząc na to zdjęcie, wielu widziało w nim kapelusz dziecięcy, który nosił Buratino, gofrowany kubek z lodami w kształcie klaksonu lub ostrzegawczy pomarańczowy i czarny pasiasty stożek drogowy.

Stożek elementów geometrycznych
Aby lepiej zrozumieć kwestię tego, czym jest stożek, należy przytoczyć geometryczne nazwy elementów tej postaci przestrzennej.
Stożek jest ograniczony dwiema powierzchniami. Pierwszy nazywa się podstawą. Jest to płaszczyzna, która jest ograniczona przez krzywą opisaną powyżej. Na przykład może to być okrąg lub elipsa. Druga powierzchnia jest bokiem kształtu i jest nazywana stożkową. Nie leży on w tej samej płaszczyźnie, ale może zostać przekształcony w postać płaską, co zostanie omówione poniżej.
Jednym z ważnych elementów stożka jest jego wierzchołek. Ten punkt wiąże stożkową powierzchnię. Wszystkie punkty krzywej bazowej są z nią połączone.
Segment łączący szczyt podstawy, nazywany generatrix lub tworzący stożek. Z kolei krzywa ograniczająca podstawę została nazwana dyrektorem lub figurą przewodnika.
Obszary stożkowej powierzchni i podstawy sumują się do całkowitej powierzchni stożka. Objętość przestrzeni, którą ograniczają te dwie powierzchnie, to objętość stożka.
Okrągły prosty stożek i jego liniowa charakterystyka
Powyżej podano ogólną definicję stożka. Niemniej jednak, często w praktyce i problemach geometrycznych istnieje specyficzna forma tej figury - prosty, okrągły stożek. Pokazano to poniżej.
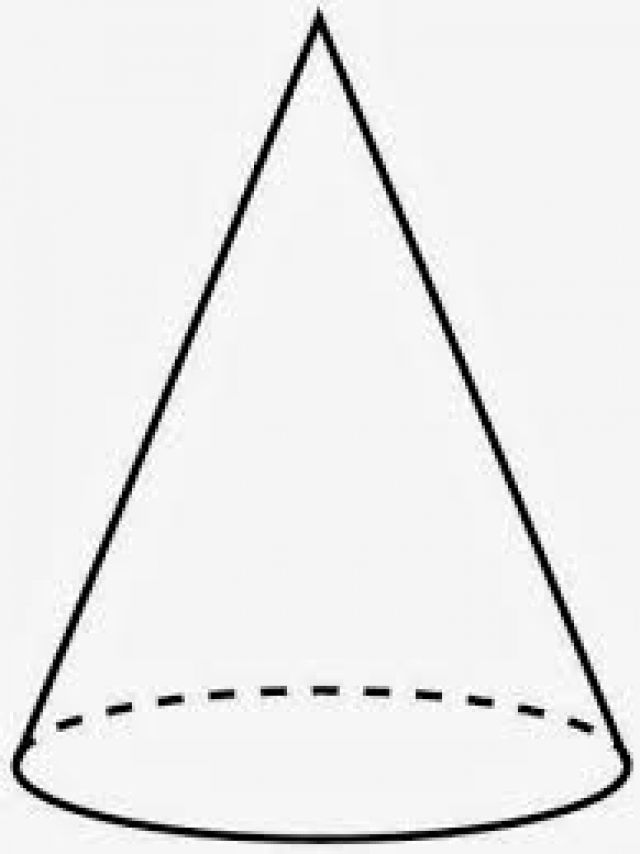
Podstawą tej figury jest krąg. Nazywa się to prostym, ponieważ prostopadła spadła do podstawy z wysokości przecina koło w jego dokładnym środku. Jeśli ten warunek nie zostanie spełniony, możemy mówić o nachylonym stożku.
Linia łącząca wierzchołek ze środkiem okręgu nazywana jest osią figury. Jest to również oś obrotu stożka. Rzeczywiście, jeśli weźmiesz trójkąt prostokątny i zaczniesz go obracać wokół jednej z nóg, wynikowa figura będzie prostym stożkiem z okrągłą podstawą. Ten sposób otrzymywania stożka pokazano schematycznie poniżej.
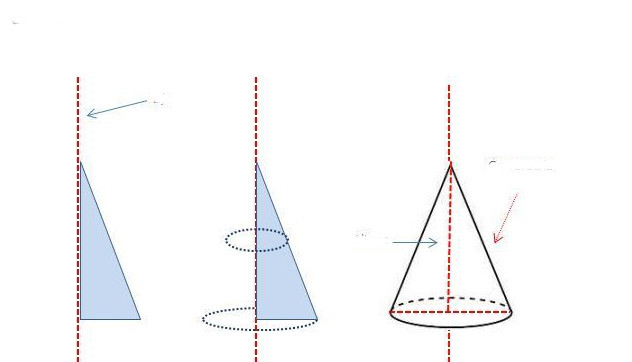
Można zauważyć, że generator będzie równy długości przeciwprostokątnej trójkąta. Noga, wokół której dokonano obrotu, stanie się wysokością trójwymiarowej figury, a druga noga będzie równa promieniowi stożka (promień okrągłej podstawy).
Jedną z ważnych cech danej figury jest to, że długości wszystkich generatorów dla niej są sobie równe. Fakt ten pozwala nam, używając twierdzenia Pitagorasa, zapisać matematyczne połączenie pomiędzy trzema głównymi liniowymi parametrami kształtu:
g 2 = r 2 + h 2
Kwadrat generatora o prostym okrągłym stożku g jest równy sumie kwadratów jego promienia r i wysokości h.
Po zbadaniu kwestii, jaki stożek jest linią prostą z okrągłą podstawą, pokażemy, w jaki sposób jego powierzchnia i objętość są możliwe.
Określenie powierzchni
Jak już zauważono, powierzchnia figury jest utworzona przez stożkową powierzchnię i płaską podstawę. Jaki jest ich obszar? Z pewnością możesz odpowiedzieć na to pytanie, jeśli spojrzysz na płaski skan okrągłego stożka. Odcinając podstawę od powierzchni bocznej i przecinając ją wzdłuż tworzącej, otrzymujemy następujący wynik.
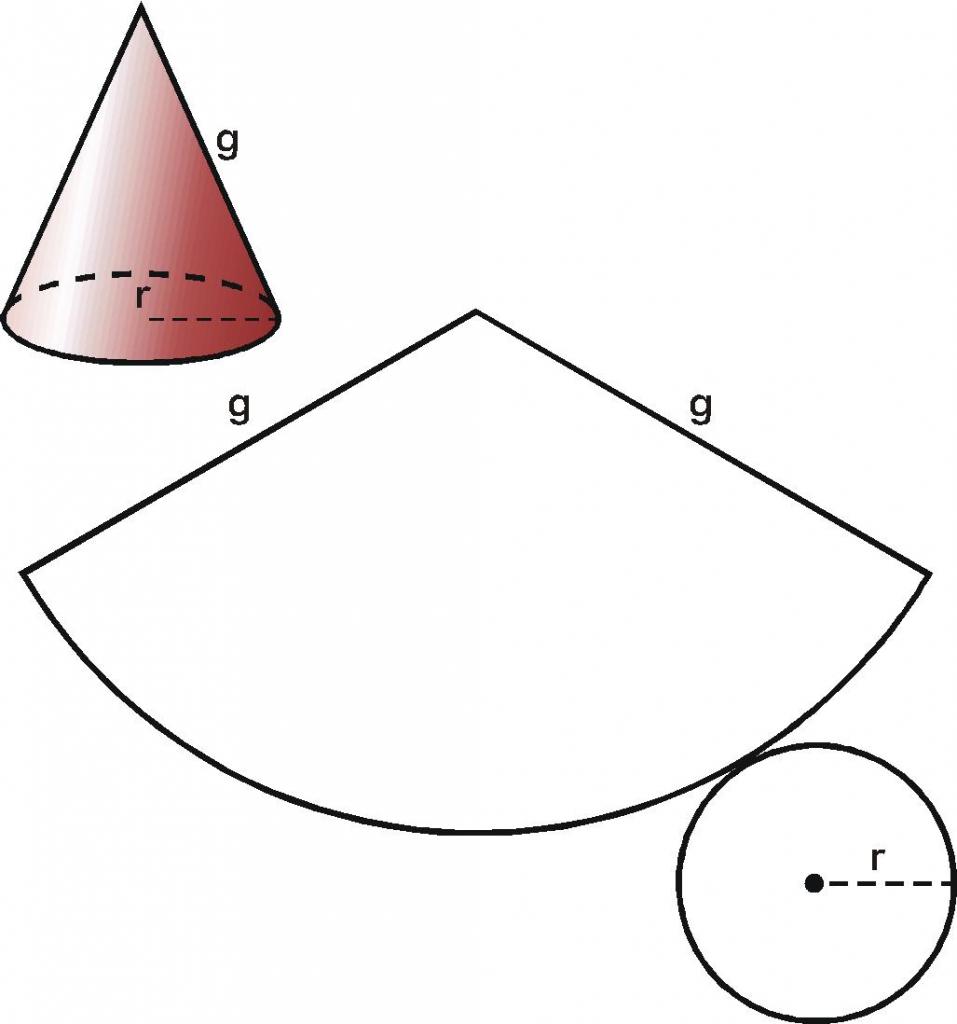
Nie ma problemów z określeniem obszaru koła. Formuła dla tego obszaru jest znana każdemu uczniowi. Zapisz:
S o = pi * r 2
Symbol S o to obszar podstawy figury.
Boczna powierzchnia stożka na płaskim skanie jest reprezentowana przez okrągły sektor, którego promień jest równy długości generatora, a długość łuku, na którym spoczywa sektor, jest równa długości obwodu podstawy. Dane te pozwalają nam jednoznacznie określić obszar sektora. Nie podamy pośrednich obliczeń dla uzyskania wzoru na kwadrat S b powierzchni bocznej stożka. Piszemy końcowy wynik:
S b = pi * g * r
Ponieważ generatrix g jest zawsze większa niż promień r, powierzchnia bocznej powierzchni figury będzie, dla dowolnych parametrów, przekraczać powierzchnię podstawy.
Wzór na całkowity obszar ma postać:
S = S o + S b = pi * r * (r + g)
Określanie objętości figury
Czytelnicy mogli zauważyć, że kształt stożka przypomina coś w rodzaju piramidy, a jedynie jego powierzchnia boczna jest gładka i pozbawiona żeber, niczym piramida. Ta analogia ma uzasadnienie geometryczne, ponieważ wzrost liczby bocznych ścian piramidy w nieskończoność przekłada ją na stożek. Fakt ten pozwala na zapisanie objętości stożka dokładnie takiej samej, jak w przypadku objętości piramidy. Mamy:
V = 1/3 * h * S o
Zauważ, że nie ma znaczenia, która zamknięta krzywa tworzy podstawę stożka, również nie ma znaczenia, czy figura jest prosta czy ukośna, wzór będzie ważny we wszystkich tych przypadkach.
Dla stożka rundy wyrażenie dla V przyjmuje konkretną postać:
V = 1/3 * pi * r 2 * godz
Zadaniem określenia obszaru stożka poprzez jego objętość
Pokazujemy, jak korzystać z pisemnych formuł.
Załóżmy, że objętość okrągłego stożka wynosi 50 cm 3 . Konieczne jest obliczenie jego powierzchni, jeśli promień r jest trzy razy mniejszy niż wysokość h.
Piszemy wzór na objętość i relację wysokości h z promieniem r zgodnie ze stanem problemu:
V = 1/3 * pi * r 2 * h;
h = 3 * r.
Z tych równań otrzymujemy:
V = 1/3 * pi * r 2 * 3 * r =>
r = (V / pi) ≈ 2,516 cm;
h = 3 * ∛ (V / pi) ≈ 7,547 cm.
Uzyskane wartości pozwalają nam obliczyć długość generatora generalnego stożka g:
g = √ (h 2 + r 2 ) = 7,955 cm.
Wzór na powierzchnię tego rysunku to:
S = pi * r * (r + g)
Ustaliliśmy wszystkie niezbędne ilości (r i g). Zastępując ich wartości liczbowe równością, otrzymujemy odpowiedź: S = 82,72 cm 2 .